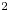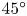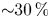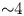1. Introduction
Laser-driven proton acceleration using ultraintense pulses has been an active field of research in the past two decades (Tikhonchuk Reference Tikhonchuk2010; Daido, Nishiuchi & Pirozhkov Reference Daido, Nishiuchi and Pirozhkov2012; Macchi, Borghesi & Passoni Reference Macchi, Borghesi and Passoni2013). The strong electric fields produced in the interaction of the ultraintense laser pulse with solid targets can accelerate protons to high energies on acceleration distances of only a few microns. This has led to the implementation or exploration on small-scale facilities of a large variety of applications, such as radiography (Romagnani et al. Reference Romagnani, Fuchs, Borghesi, Antici, Audebert, Ceccherini, Cowan, Grismayer, Kar and Macchi2005), generation of warm dense matter (Patel et al. Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003; Pelka et al. Reference Pelka, Gregori, Gericke, Vorberger, Glenzer, Günther, Harres, Heathcote, Kritcher and Kugland2010), inertial confinement fusion (Roth et al. Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely and Wilks2001), nuclear physics (McKenna et al. Reference McKenna, Ledingham, McCanny, Singhal, Spencer, Santala, Beg, Krushelnick, Tatarakis and Wei2003) or proton therapy (Bulanov & Khoroshkov Reference Bulanov and Khoroshkov2002). The most investigated, and routinely exploited, mechanism is the so-called target normal sheath acceleration (TNSA), which benefits from a relatively easy implementation (Clark et al. Reference Clark, Krushelnick, Zepf, Beg, Tatarakis, Machacek, Santala, Watts, Norreys and Dangor2000; Maksimchuk et al. Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov2000; Snavely et al. Reference Snavely, Key, Hatchett, Cowan, Roth, Phillips, Stoyer, Henry, Sangster and Singh2000; Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001). TNSA, however, yields maximum ion energies E max that scale rather weakly with the laser intensity I 0 (![]() $E_\textrm {max} \propto I_0^{\alpha }$, with
$E_\textrm {max} \propto I_0^{\alpha }$, with ![]() $\alpha \simeq 0.5\!-\!1$ depending on the laser duration) (Zeil et al. Reference Zeil, Kraft, Bock, Bussmann, Cowan, Kluge, Metzkes, Richter, Sauerbrey and Schramm2010). This limitation motivates the investigation of alternative, possibly more efficient schemes, e.g. radiation pressure (or light-sail) acceleration (Esirkepov et al. Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Kar et al. Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely and Osterholz2012), shock acceleration (Silva et al. Reference Silva, Marti, Davies, Fonseca, Ren, Tsung and Mori2004; Haberberger et al. Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012) (with
$\alpha \simeq 0.5\!-\!1$ depending on the laser duration) (Zeil et al. Reference Zeil, Kraft, Bock, Bussmann, Cowan, Kluge, Metzkes, Richter, Sauerbrey and Schramm2010). This limitation motivates the investigation of alternative, possibly more efficient schemes, e.g. radiation pressure (or light-sail) acceleration (Esirkepov et al. Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Kar et al. Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely and Osterholz2012), shock acceleration (Silva et al. Reference Silva, Marti, Davies, Fonseca, Ren, Tsung and Mori2004; Haberberger et al. Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012) (with ![]() $E_\textrm {max}\propto I_0$), directed Coulomb explosion (Bulanov et al. Reference Bulanov, Brantov, Bychenkov, Chvykov, Kalinchenko, Matsuoka, Rousseau, Reed, Yanovsky and Litzenberg2008) or breakout afterburner (Yin et al. Reference Yin, Albright, Hegelich and Fernández2006).
$E_\textrm {max}\propto I_0$), directed Coulomb explosion (Bulanov et al. Reference Bulanov, Brantov, Bychenkov, Chvykov, Kalinchenko, Matsuoka, Rousseau, Reed, Yanovsky and Litzenberg2008) or breakout afterburner (Yin et al. Reference Yin, Albright, Hegelich and Fernández2006).
The possibility of employing several laser pulses to control the preplasma formation and improve the general efficiency of the TNSA process has been studied in experiments (Markey et al. Reference Markey, McKenna, Brenner, Carroll, Günther, Harres, Kar, Lancaster, Nürnberg and Quinn2010; Scott et al. Reference Scott, Green, Bagnoud, Brabetz, Brenner, Carroll, MacLellan, Robinson, Roth and Spindloe2012; Brenner et al. Reference Brenner, Robinson, Markey, Scott, Gray, Rosinski, Deppert, Badziak, Batani and Davies2014; Ferri et al. Reference Ferri, Senje, Dalui, Svensson, Aurand, Hansson, Persson, Lundh, Wahlström and Gremillet2018). In particular, in a recent work, we studied the influence of splitting the laser pulse in two pulses containing each half of the total energy in a TNSA set-up (Ferri, Siminos & Fülöp Reference Ferri, Siminos and Fülöp2019). In that work, the half-pulses were simultaneously focused onto a few-![]() $\mathrm {\mu }\textrm {m}$ thick target, but at opposite incidence angles. Through particle-in-cell (PIC) simulations, we showed that the proton energy could be increased in the two-pulse scheme by approximately 80 % with lasers impinging at
$\mathrm {\mu }\textrm {m}$ thick target, but at opposite incidence angles. Through particle-in-cell (PIC) simulations, we showed that the proton energy could be increased in the two-pulse scheme by approximately 80 % with lasers impinging at ![]() ${\pm }45^\circ$ angles onto a foil target with sub-wavelength density scale length. Such enhancement was found to result from a more efficient, Brunel-type vacuum heating of the electrons, due to the laser interference, and the ensuing suppression of the mitigating
${\pm }45^\circ$ angles onto a foil target with sub-wavelength density scale length. Such enhancement was found to result from a more efficient, Brunel-type vacuum heating of the electrons, due to the laser interference, and the ensuing suppression of the mitigating ![]() $v\times B$ force (with
$v\times B$ force (with ![]() $v $ the particle velocity and B the magnetic field), at the target surface (Geindre, Audebert & Marjoribanks Reference Geindre, Audebert and Marjoribanks2006).
$v $ the particle velocity and B the magnetic field), at the target surface (Geindre, Audebert & Marjoribanks Reference Geindre, Audebert and Marjoribanks2006).
While those results are very promising for TNSA experiments, notably those performed at ultrahigh laser contrast (Ceccotti et al. Reference Ceccotti, Lévy, Popescu, Réau, D'Oliveira, Monot, Geindre, Lefebvre and Martin2007), they also suggest possible improvements for other acceleration set-ups, especially those involving ultrathin (nanometric) target foils. Previous studies indeed demonstrated that, in the case of femtosecond laser pulses, proton energies are maximized for target thicknesses such that relativistic self-induced transparency (RSIT) occurs near the laser peak (Esirkepov, Yamagiwa & Tajima Reference Esirkepov, Yamagiwa and Tajima2006; d'Humières et al. Reference d'Humières, Brantov, Bychenkov and Tikhonchuk2013; Brantov et al. Reference Brantov, Govras, Bychenkov and Rozmus2015). It is therefore worth exploring whether the use of two interfering half-pulses in this regime could significantly enhance the hot-electron generation, and hence lower the RSIT threshold.
In this work, therefore, we investigate, by means of PIC numerical simulations, how splitting the laser pulse into two half-pulses focused at opposite incidence angles affects the interaction with nanometric foils. For the purpose of establishing a reference case, we first investigate the dynamics of ![]() $\textrm {CH}_2$ foils driven by a single ultraintense laser pulse under normal or oblique incidence. While the latter case leads to higher proton energies due to stronger electron heating, the optimum foil target is approximately twice thinner than that found at normal incidence, a consequence of self-induced magnetostatic fields within the ion acceleration region. Secondly, we find that, by further enhancing the electron heating and mitigating the growth of the deleterious magnetostatic fields, the two-pulse scheme significantly increases the cutoff energy and number of the accelerated protons. It may also facilitate experimental investigations of RSIT-related processes by allowing thicker targets to turn relativistically transparent.
$\textrm {CH}_2$ foils driven by a single ultraintense laser pulse under normal or oblique incidence. While the latter case leads to higher proton energies due to stronger electron heating, the optimum foil target is approximately twice thinner than that found at normal incidence, a consequence of self-induced magnetostatic fields within the ion acceleration region. Secondly, we find that, by further enhancing the electron heating and mitigating the growth of the deleterious magnetostatic fields, the two-pulse scheme significantly increases the cutoff energy and number of the accelerated protons. It may also facilitate experimental investigations of RSIT-related processes by allowing thicker targets to turn relativistically transparent.
2. Proton acceleration at normal or oblique laser incidence in relativistically transparent foils
According to previous works (Esirkepov et al. Reference Esirkepov, Yamagiwa and Tajima2006; d'Humières et al. Reference d'Humières, Brantov, Bychenkov and Tikhonchuk2013; Brantov et al. Reference Brantov, Govras, Bychenkov and Rozmus2015), maximum ion energies attained by femtosecond laser pulses are achieved for target thicknesses close to the RSIT threshold, ![]() $l_\textrm {opt} \simeq \lambda _0 a_0 n_c/2n_e$, where
$l_\textrm {opt} \simeq \lambda _0 a_0 n_c/2n_e$, where ![]() $\lambda _0$ and
$\lambda _0$ and ![]() $a_0$ are, respectively, the laser wavelength and maximum potential vector,
$a_0$ are, respectively, the laser wavelength and maximum potential vector, ![]() $n_c$ is the critical density and
$n_c$ is the critical density and ![]() $n_e$ is the electron density of the target.
$n_e$ is the electron density of the target.
Our simulations have been performed in two-dimensional (2-D) geometry using the PIC code epoch (Arber et al. Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell2015). As a reference configuration, we have first considered a single laser pulse of ![]() $16\ \textrm {J}$ energy and
$16\ \textrm {J}$ energy and ![]() $0.8\ \mathrm {\mu }\textrm {m}$ wavelength, interacting at normal incidence with a solid-density
$0.8\ \mathrm {\mu }\textrm {m}$ wavelength, interacting at normal incidence with a solid-density ![]() $\textrm {CH}_2$ foil. The pulse is
$\textrm {CH}_2$ foil. The pulse is ![]() $p$-polarized (i.e. along the
$p$-polarized (i.e. along the ![]() $y$ axis), has Gaussian transverse and temporal profiles of FWHM (full width half maximum)
$y$ axis), has Gaussian transverse and temporal profiles of FWHM (full width half maximum) ![]() $w_0=7\ \mathrm {\mu }\textrm {m}$ and
$w_0=7\ \mathrm {\mu }\textrm {m}$ and ![]() $\tau _0 =38\ \textrm {fs}$, respectively and a peak intensity
$\tau _0 =38\ \textrm {fs}$, respectively and a peak intensity ![]() $I_0 = 5\times 10^{20}\ \textrm {W}\,\textrm {cm}^{-2}$ (
$I_0 = 5\times 10^{20}\ \textrm {W}\,\textrm {cm}^{-2}$ (![]() $a_0 \simeq 15$). The reference time
$a_0 \simeq 15$). The reference time ![]() $t=0$ corresponds to the pulse maximum reaching the target. The CH
$t=0$ corresponds to the pulse maximum reaching the target. The CH![]() $_2$ target is modelled as a fully ionized plasma at a
$_2$ target is modelled as a fully ionized plasma at a ![]() $1.1\ \textrm {g}\,\textrm {cm}^{-3}$ density, corresponding to a total electron density
$1.1\ \textrm {g}\,\textrm {cm}^{-3}$ density, corresponding to a total electron density ![]() $n_e = 220n_c$. Its thickness,
$n_e = 220n_c$. Its thickness, ![]() $l$, is varied in a range,
$l$, is varied in a range, ![]() $20 \le l \le 60\ \textrm {nm}$, encompassing the predicted optimum,
$20 \le l \le 60\ \textrm {nm}$, encompassing the predicted optimum, ![]() $l_\textrm {opt} = 30\ \textrm {nm}$. We use 200 particles per cell and per species. The simulation domain has dimensions of
$l_\textrm {opt} = 30\ \textrm {nm}$. We use 200 particles per cell and per species. The simulation domain has dimensions of ![]() $75\times 80\ \mathrm {\mu } \textrm {m}^2$ with mesh size
$75\times 80\ \mathrm {\mu } \textrm {m}^2$ with mesh size ![]() $\Delta x \times \Delta y = 4 \times 10\ \textrm {nm}^2$.
$\Delta x \times \Delta y = 4 \times 10\ \textrm {nm}^2$.
Figure 1(a,b) plots (as black solid curves) the target thickness dependence of the (a) maximum proton energy and (b) the number of high-energy (above 30 MeV) protons, as measured at the final simulation time (![]() $t_\textrm {max}=300\ \textrm {fs}$). Both quantities are found to be maximized at
$t_\textrm {max}=300\ \textrm {fs}$). Both quantities are found to be maximized at ![]() $l=40\ \textrm {nm}$, close to
$l=40\ \textrm {nm}$, close to ![]() $l_\textrm {opt}$, with proton energies as high as
$l_\textrm {opt}$, with proton energies as high as ![]() ${\sim } 100\ \textrm {MeV}$ being then recorded. The number of high-energy protons is more sensitive to the target thickness than their maximum energy. Using
${\sim } 100\ \textrm {MeV}$ being then recorded. The number of high-energy protons is more sensitive to the target thickness than their maximum energy. Using ![]() $l=20\ \textrm {nm}$ or
$l=20\ \textrm {nm}$ or ![]() $60\ \textrm {nm}$ leads to a decrease in the proton number by a factor of 2 to 3 compared to the optimum case.
$60\ \textrm {nm}$ leads to a decrease in the proton number by a factor of 2 to 3 compared to the optimum case.

Figure 1. Ion acceleration by a single, ![]() $16\ \textrm {J}$ energy,
$16\ \textrm {J}$ energy, ![]() $38\ \textrm {fs}$ duration laser pulse as a function of the
$38\ \textrm {fs}$ duration laser pulse as a function of the ![]() $\textrm {CH}_2$ foil thickness: (a) maximum proton energy and (b) number of protons with
$\textrm {CH}_2$ foil thickness: (a) maximum proton energy and (b) number of protons with ![]() ${>}30\ \textrm {MeV}$ energies. The laser pulse is either normally incident (solid black) or obliquely incident at a
${>}30\ \textrm {MeV}$ energies. The laser pulse is either normally incident (solid black) or obliquely incident at a ![]() $45^\circ$ angle (dashed blue).
$45^\circ$ angle (dashed blue).
The optimum acceleration conditions are reached when RSIT occurs near the laser peak, which is confirmed by looking at the laser fields going through the target in figure 2(a–c), and by computing, for each thickness value, the transmitted (![]() $C_T$), reflected (
$C_T$), reflected (![]() $C_T$) and absorbed (
$C_T$) and absorbed (![]() $C_A$) fractions of the laser energy. While the laser pulse is significantly transmitted (
$C_A$) fractions of the laser energy. While the laser pulse is significantly transmitted (![]() $C_T \simeq 0.53$) and relatively weakly absorbed (
$C_T \simeq 0.53$) and relatively weakly absorbed (![]() $C_A \simeq 0.12$) through the
$C_A \simeq 0.12$) through the ![]() $20\ \textrm {nm}$ foil (figure 2a), it gets significantly reflected (
$20\ \textrm {nm}$ foil (figure 2a), it gets significantly reflected (![]() $C_R \simeq 0.55$) when the foil thickness is increased to
$C_R \simeq 0.55$) when the foil thickness is increased to ![]() $40\ \textrm {nm}$ (figure 2b), while its absorption is approximately doubled (
$40\ \textrm {nm}$ (figure 2b), while its absorption is approximately doubled (![]() $C_A\simeq 0.23$). If the foil thickness is further increased to
$C_A\simeq 0.23$). If the foil thickness is further increased to ![]() $60\ \textrm {nm}$, the laser absorption remains similar,
$60\ \textrm {nm}$, the laser absorption remains similar, ![]() $C_A \simeq 0.24$, but the transmission drops to a very low value,
$C_A \simeq 0.24$, but the transmission drops to a very low value, ![]() $C_T \simeq 0.04$ (figure 2c). As a result of the RSIT then taking place late in the decreasing part of the pulse, the expanding protons no longer benefit from the boost in energy caused by volumetric electron heating at the laser peak (Mishra, Fiuza & Glenzer Reference Mishra, Fiuza and Glenzer2018), and hence experience a weaker overall acceleration. This corresponds to the transition to the TNSA regime. Note that for our parameters, and because of the foil rapidly turning transparent to the laser light, radiation pressure plays a minor role in the acceleration of the fastest ions.
$C_T \simeq 0.04$ (figure 2c). As a result of the RSIT then taking place late in the decreasing part of the pulse, the expanding protons no longer benefit from the boost in energy caused by volumetric electron heating at the laser peak (Mishra, Fiuza & Glenzer Reference Mishra, Fiuza and Glenzer2018), and hence experience a weaker overall acceleration. This corresponds to the transition to the TNSA regime. Note that for our parameters, and because of the foil rapidly turning transparent to the laser light, radiation pressure plays a minor role in the acceleration of the fastest ions.

Figure 2. Transverse electric field ![]() $E_y$ (in
$E_y$ (in ![]() $\textrm {V}\,\textrm {m}^{-1}$) at
$\textrm {V}\,\textrm {m}^{-1}$) at ![]() $t=45\ \textrm {fs}$ after the on-target laser peak, for foil thicknesses (a)
$t=45\ \textrm {fs}$ after the on-target laser peak, for foil thicknesses (a) ![]() $l=20\ \textrm {nm}$, (b)
$l=20\ \textrm {nm}$, (b) ![]() $l=40\ \textrm {nm}$ (b) and (c)
$l=40\ \textrm {nm}$ (b) and (c) ![]() $60\ \textrm {nm}$. In each panel the transmitted (
$60\ \textrm {nm}$. In each panel the transmitted (![]() $C_T$), reflected (
$C_T$), reflected (![]() $C_R$) and absorbed (
$C_R$) and absorbed (![]() $C_A$) fractions of the laser energy are noted, and the dashed black line indicates the initial position of the foil.
$C_A$) fractions of the laser energy are noted, and the dashed black line indicates the initial position of the foil.
The absorption processes, and therefore the onset of RSIT, are expected to be altered when operating at oblique laser incidence. To assess the dependency of ion acceleration on the incidence angle, we now consider a laser pulse impinging at an angle ![]() $\theta = 45^\circ$ onto the foil, all other physical parameters being kept constant. The simulation domain is also enlarged to
$\theta = 45^\circ$ onto the foil, all other physical parameters being kept constant. The simulation domain is also enlarged to ![]() $75 \times 120\ \mathrm {\mu } \textrm {m}^2$. Figure 1(a,b) shows (as blue dashed curves) that the optimum target thickness in terms of the maximum proton energy (respectively proton number above
$75 \times 120\ \mathrm {\mu } \textrm {m}^2$. Figure 1(a,b) shows (as blue dashed curves) that the optimum target thickness in terms of the maximum proton energy (respectively proton number above ![]() $30\ \textrm {MeV}$) then drops from
$30\ \textrm {MeV}$) then drops from ![]() $l=40\ \textrm {nm}$ to
$l=40\ \textrm {nm}$ to ![]() $20\ \textrm {nm}$ (respectively
$20\ \textrm {nm}$ (respectively ![]() $30\ \textrm {nm}$). This decrease seems reasonable since an oblique incidence angle leads to a longer path for the laser in the target, i.e. an increased effective thickness (
$30\ \textrm {nm}$). This decrease seems reasonable since an oblique incidence angle leads to a longer path for the laser in the target, i.e. an increased effective thickness (![]() $l_\textrm {eff} = l/\cos \theta$). More surprisingly, the decrease in the optimum target thickness goes along with a significant enhancement of the proton cutoff energy (by
$l_\textrm {eff} = l/\cos \theta$). More surprisingly, the decrease in the optimum target thickness goes along with a significant enhancement of the proton cutoff energy (by ![]() ${\sim }15\,\%$, up to
${\sim }15\,\%$, up to ![]() ${\sim } 120\ \textrm {MeV}$) and number (by
${\sim } 120\ \textrm {MeV}$) and number (by ![]() ${\sim }60\,\%$).
${\sim }60\,\%$).
The improvement of the proton acceleration at oblique incidence can be explained by a more efficient mechanism for hot-electron generation. The absorption and transmission coefficients for the normal and oblique incidence are summarized in figure 3(a), showing an overall (approximately twofold) increase in the absorption coefficient at oblique incidence. For instance, the absorption coefficient at ![]() $l=40\ \textrm {nm}$ rises from
$l=40\ \textrm {nm}$ rises from ![]() $C_A \simeq 0.23$ at
$C_A \simeq 0.23$ at ![]() $\theta =0^\circ$ to
$\theta =0^\circ$ to ![]() $C_A \simeq 0.40$ at
$C_A \simeq 0.40$ at ![]() $\theta = 45^\circ$. By contrast, the transmission coefficient vs. thickness values are similar at
$\theta = 45^\circ$. By contrast, the transmission coefficient vs. thickness values are similar at ![]() $\theta = 0^\circ$ and
$\theta = 0^\circ$ and ![]() $45^\circ$ indicating that the transparency condition weakly depends on the incidence angle.
$45^\circ$ indicating that the transparency condition weakly depends on the incidence angle.

Figure 3. (a) Absorption (![]() $C_A$, crosses) and transmission (
$C_A$, crosses) and transmission (![]() $C_T$, squares) coefficients for normal (black) and oblique (blue) incidence as a function of the target thickness. (b) Electron energy distribution recorded at
$C_T$, squares) coefficients for normal (black) and oblique (blue) incidence as a function of the target thickness. (b) Electron energy distribution recorded at ![]() $t=20\ \textrm {fs}$ after the on-target laser peak; black and blue curves correspond to normal and oblique (
$t=20\ \textrm {fs}$ after the on-target laser peak; black and blue curves correspond to normal and oblique (![]() $45^\circ$) laser incidence, while solid and dashed curves correspond to
$45^\circ$) laser incidence, while solid and dashed curves correspond to ![]() $40\ \textrm {nm}$ and
$40\ \textrm {nm}$ and ![]() $20\ \textrm {nm}$ thick targets.
$20\ \textrm {nm}$ thick targets.
Figure 3(b) plots the electron energy spectra recorded ![]() $20\ \textrm {fs}$ after the on-target pulse maximum for two values of the target thickness (
$20\ \textrm {fs}$ after the on-target pulse maximum for two values of the target thickness (![]() $l=20$ and
$l=20$ and ![]() $40\ \textrm {nm}$). They show that the higher laser absorption found at oblique incidence translates into an increase in both the number and temperature of the hot (
$40\ \textrm {nm}$). They show that the higher laser absorption found at oblique incidence translates into an increase in both the number and temperature of the hot (![]() ${>}1\ \textrm {MeV}$) electrons. The thicker (40 nm) target seems to mainly boost the number of hot electrons in both cases.
${>}1\ \textrm {MeV}$) electrons. The thicker (40 nm) target seems to mainly boost the number of hot electrons in both cases.
To understand the simulation results we adapt the thin-foil expansion model proposed in Brantov et al. (Reference Brantov, Govras, Bychenkov and Rozmus2015) to the simulated scenario. This model considers the expansion of a neutral plasma slab of initial thickness ![]() $l$ and uniform ion density
$l$ and uniform ion density ![]() $n_{i0}$, composed of a single ion species. It assumes a Boltzmann electron distribution,
$n_{i0}$, composed of a single ion species. It assumes a Boltzmann electron distribution, ![]() $n_e(x,t) = n_e(0,t) \exp [e \phi (x,t)/T_e(t)]$, where
$n_e(x,t) = n_e(0,t) \exp [e \phi (x,t)/T_e(t)]$, where ![]() $\phi (x,t)$ is the electrostatic potential,
$\phi (x,t)$ is the electrostatic potential, ![]() $T_e(t)$ is the (longitudinal) electron temperature and
$T_e(t)$ is the (longitudinal) electron temperature and ![]() $n_e(0,t)$ is the (time-decreasing) electron density at the target centre (
$n_e(0,t)$ is the (time-decreasing) electron density at the target centre (![]() $x=0$). The assumption of a single ion species and the choice of a Maxwell–Boltzmann distribution for the electrons may seem overly simplified, yet as it will be shown below, despite these approximations, the model is able to capture the salient features of ion acceleration from thin foils, as already observed in Brantov et al. (Reference Brantov, Govras, Bychenkov and Rozmus2015). The electrostatic field
$x=0$). The assumption of a single ion species and the choice of a Maxwell–Boltzmann distribution for the electrons may seem overly simplified, yet as it will be shown below, despite these approximations, the model is able to capture the salient features of ion acceleration from thin foils, as already observed in Brantov et al. (Reference Brantov, Govras, Bychenkov and Rozmus2015). The electrostatic field ![]() $E_x = -\partial _x \phi$ is taken to vary linearly inside the ion-filled region:
$E_x = -\partial _x \phi$ is taken to vary linearly inside the ion-filled region: ![]() $E_x(x,t) = E_f x/x_f(t)$ for
$E_x(x,t) = E_f x/x_f(t)$ for ![]() $0 \le x \le x_f(t)$, where
$0 \le x \le x_f(t)$, where ![]() $x_f(t)$ is the position of the ion front [
$x_f(t)$ is the position of the ion front [![]() $x_f(0)=l/2$] and
$x_f(0)=l/2$] and ![]() $E_f(t)$ is the field strength at the ion front. From this it readily follows that
$E_f(t)$ is the field strength at the ion front. From this it readily follows that ![]() $\phi (x,t) = -E_f(t) x^2/2x_f(t)$. Outside the ion cloud (
$\phi (x,t) = -E_f(t) x^2/2x_f(t)$. Outside the ion cloud (![]() $x>x_f$), the electric potential obeys the nonlinear Poisson equation,
$x>x_f$), the electric potential obeys the nonlinear Poisson equation, ![]() $\partial _{xx} \phi = en_e(0,t) \exp (e\phi /T_e)/\epsilon _0$, where e is the elementary charge and
$\partial _{xx} \phi = en_e(0,t) \exp (e\phi /T_e)/\epsilon _0$, where e is the elementary charge and ![]() $\epsilon _0$ the vacuum permittivity. Multiplying this equation by
$\epsilon _0$ the vacuum permittivity. Multiplying this equation by ![]() $\partial _x \phi$ and integrating it over
$\partial _x \phi$ and integrating it over ![]() $[x_f,\infty ]$ yields
$[x_f,\infty ]$ yields ![]() $n_e(0,t) = ( \epsilon _0 E_f^2/2T_e) \exp (eE_f x_f/2 T_e)$. Furthermore, integrating Gauss's equation over
$n_e(0,t) = ( \epsilon _0 E_f^2/2T_e) \exp (eE_f x_f/2 T_e)$. Furthermore, integrating Gauss's equation over ![]() $[0,x_f]$ gives
$[0,x_f]$ gives
 \begin{align} E_f(t) &= \frac{Z e n_{i0}l}{2\epsilon_0} - \frac{e n_e(0,t)}{\epsilon_0} \int_0^{x_f} \textrm{d}x\exp({e \phi/T_e}) \nonumber\\ &= \frac{Z e n_{i0}l}{2\epsilon_0} - \frac{e E_f^2}{2T_e} \exp({eE_f x_f/2T}) \int_0^{x_f} \textrm{d}x\exp({-eE_fx^2/2x_f T_e}), \end{align}
\begin{align} E_f(t) &= \frac{Z e n_{i0}l}{2\epsilon_0} - \frac{e n_e(0,t)}{\epsilon_0} \int_0^{x_f} \textrm{d}x\exp({e \phi/T_e}) \nonumber\\ &= \frac{Z e n_{i0}l}{2\epsilon_0} - \frac{e E_f^2}{2T_e} \exp({eE_f x_f/2T}) \int_0^{x_f} \textrm{d}x\exp({-eE_fx^2/2x_f T_e}), \end{align}
where ![]() $Z$ is the ion charge state. Introducing
$Z$ is the ion charge state. Introducing ![]() $\mathrm {erf}(z)$ the error function, the above equation can be recast as
$\mathrm {erf}(z)$ the error function, the above equation can be recast as
 \begin{equation} E_f(t) = \frac{Zen_{i0}l}{2 \epsilon_0} - \frac{\sqrt{{\rm \pi}} E_f}{2} \sqrt{\frac{e E_f x_f }{2 T_e}} \mathrm{erf} \left( \sqrt{\frac{e E_f x_f }{2 T_e}}\right) . \end{equation}
\begin{equation} E_f(t) = \frac{Zen_{i0}l}{2 \epsilon_0} - \frac{\sqrt{{\rm \pi}} E_f}{2} \sqrt{\frac{e E_f x_f }{2 T_e}} \mathrm{erf} \left( \sqrt{\frac{e E_f x_f }{2 T_e}}\right) . \end{equation}
This formula assumes a 1-D expansion geometry, and hence should overestimate the field strength when the ion front has moved a distance comparable with the transverse size of the sheath field (![]() ${\sim } w_0 \cos \theta$). A correction factor is thus applied to account for this effect
${\sim } w_0 \cos \theta$). A correction factor is thus applied to account for this effect
 \begin{equation} E_{f,\delta}(t) = \frac{E_f(t)}{\left[ 1+ \left(\dfrac{2 x_f(t)}{w_0 \cos \theta} \right)^2\right]^{(\delta -1)/2}}, \end{equation}
\begin{equation} E_{f,\delta}(t) = \frac{E_f(t)}{\left[ 1+ \left(\dfrac{2 x_f(t)}{w_0 \cos \theta} \right)^2\right]^{(\delta -1)/2}}, \end{equation}
where ![]() $\delta \in (2,3)$ is the spatial dimensionality of the problem (
$\delta \in (2,3)$ is the spatial dimensionality of the problem (![]() $\delta =2$ in the simulation geometry).
$\delta =2$ in the simulation geometry).
The electron temperature ![]() $T_e(t)$ is assumed to follow the rise in the laser intensity
$T_e(t)$ is assumed to follow the rise in the laser intensity ![]() $I_0(t)$, here taken in the form
$I_0(t)$, here taken in the form ![]() $\sin ^2({\rm \pi} t/2\tau _0)$, and to stay constant in its decreasing part. The maximum electron temperature is inferred from the measured laser absorption:
$\sin ^2({\rm \pi} t/2\tau _0)$, and to stay constant in its decreasing part. The maximum electron temperature is inferred from the measured laser absorption: ![]() $T_{e,\textrm {max}}/m_ec^2 = 0.8C_A (a_0^2/2) (c \tau _0 /l \cos \theta ) (n_c/n_e)$, where the
$T_{e,\textrm {max}}/m_ec^2 = 0.8C_A (a_0^2/2) (c \tau _0 /l \cos \theta ) (n_c/n_e)$, where the ![]() $0.8$ factor corresponds to an averaging of the intensity over the laser focal spot. After the irradiation, the electrons start cooling down adiabatically. More specifically,
$0.8$ factor corresponds to an averaging of the intensity over the laser focal spot. After the irradiation, the electrons start cooling down adiabatically. More specifically, ![]() $T_e(t)$ evolves as
$T_e(t)$ evolves as
 \begin{equation} T_e(t)/T_{e,\max} = \begin{cases} \sin^2\left({\rm \pi} t/2\tau_0\right) & t \le \tau_0 \\ 1 & \tau_0 < t \le 2\tau_0 ,\\ \left[1+\left(\dfrac{c_s(t-2\tau_0)}{x_f(2\tau_0)} \right)^{\varGamma-1}\right]^{-1} & t > 2\tau_0 . \end{cases}\end{equation}
\begin{equation} T_e(t)/T_{e,\max} = \begin{cases} \sin^2\left({\rm \pi} t/2\tau_0\right) & t \le \tau_0 \\ 1 & \tau_0 < t \le 2\tau_0 ,\\ \left[1+\left(\dfrac{c_s(t-2\tau_0)}{x_f(2\tau_0)} \right)^{\varGamma-1}\right]^{-1} & t > 2\tau_0 . \end{cases}\end{equation}
We have introduced ![]() $\varGamma (T_e)$ the generalized adiabatic index for a relativistic 1-D gas and the typical sound speed
$\varGamma (T_e)$ the generalized adiabatic index for a relativistic 1-D gas and the typical sound speed ![]() $c_s = \sqrt {ZT_{e,\max }/m_i}$.
$c_s = \sqrt {ZT_{e,\max }/m_i}$.
The knowledge of ![]() $E_f(t)$ allows the velocity and position of the front ions to be advanced through
$E_f(t)$ allows the velocity and position of the front ions to be advanced through
It is to be noted that the model assumes a single ion species of charge state ![]() $Z$ and mass
$Z$ and mass ![]() $m_i = A m_p$ (
$m_i = A m_p$ (![]() $m_p$ is the proton mass). Although the expansion dynamics of light ions may be affected by that of heavier ions in a composite target (Brantov et al. Reference Brantov, Tikhonchuk, Klimo, Romanov, Ter-Avetisyan, Schnoerrer, Sokollik and Nickles2006), we will take
$m_p$ is the proton mass). Although the expansion dynamics of light ions may be affected by that of heavier ions in a composite target (Brantov et al. Reference Brantov, Tikhonchuk, Klimo, Romanov, Ter-Avetisyan, Schnoerrer, Sokollik and Nickles2006), we will take ![]() $Z=1$ and
$Z=1$ and ![]() $A=1$ in the following.
$A=1$ in the following.
Equations (2.2)–(2.5) have been solved numerically for ![]() $20 \le l \le 50\ \textrm {nm}$ and
$20 \le l \le 50\ \textrm {nm}$ and ![]() $\theta \in (0^\circ ,45^\circ )$. The results are gathered in table 1. The values obtained at normal incidence are quite close to those observed in the simulations – although generally slightly overestimated – and reproduce the same trend, with an optimal target thickness between 30 and 40 nm. At oblique incidence, however, the model consistently overestimates the maximum proton energies, especially in the thicker targets (
$\theta \in (0^\circ ,45^\circ )$. The results are gathered in table 1. The values obtained at normal incidence are quite close to those observed in the simulations – although generally slightly overestimated – and reproduce the same trend, with an optimal target thickness between 30 and 40 nm. At oblique incidence, however, the model consistently overestimates the maximum proton energies, especially in the thicker targets (![]() $l\ge 40\ \textrm {nm}$). It also predicts an optimal thickness of 30–40 nm, larger than the one (
$l\ge 40\ \textrm {nm}$). It also predicts an optimal thickness of 30–40 nm, larger than the one (![]() ${\sim }20\ \textrm {nm}$) observed in the simulations. This discrepancy between the simulations and the model suggests that the latter lacks a saturation mechanism that is mainly operative at oblique incidence and in thicker targets.
${\sim }20\ \textrm {nm}$) observed in the simulations. This discrepancy between the simulations and the model suggests that the latter lacks a saturation mechanism that is mainly operative at oblique incidence and in thicker targets.
Table 1. Maximum proton energy produced by an adaptation of the model from Brantov et al. (Reference Brantov, Govras, Bychenkov and Rozmus2015) for varying target thicknesses, at normal (![]() $E_{\max ,0^\circ }$) and oblique (
$E_{\max ,0^\circ }$) and oblique (![]() $E_{\max ,45^\circ }$) incidence.
$E_{\max ,45^\circ }$) incidence.

One such saturation-inducing effect is the generation of a strong magnetostatic field ![]() $B_z$ along the target surfaces (see figure 4a,b, associated with
$B_z$ along the target surfaces (see figure 4a,b, associated with ![]() $l=20\ \textrm {nm}$ and 40 nm), due to the electron current driven in the transverse (
$l=20\ \textrm {nm}$ and 40 nm), due to the electron current driven in the transverse (![]() $y$) direction within the plasma skin layer (Grassi et al. Reference Grassi, Grech, Amiranoff, Macchi and Riconda2017). When volumetric electron acceleration is achieved (as is the case in the RSIT regime), this field is expected to increase with the target thickness (compare figures 4a and 4b, where the
$y$) direction within the plasma skin layer (Grassi et al. Reference Grassi, Grech, Amiranoff, Macchi and Riconda2017). When volumetric electron acceleration is achieved (as is the case in the RSIT regime), this field is expected to increase with the target thickness (compare figures 4a and 4b, where the ![]() $B_z$ field strength is seen to rise from
$B_z$ field strength is seen to rise from ![]() ${\sim } 2\times 10^4\ \textrm {T}$ at
${\sim } 2\times 10^4\ \textrm {T}$ at ![]() $l=20\ \textrm {nm}$ to
$l=20\ \textrm {nm}$ to ![]() ${\sim } 4\times 10^4\ \textrm {T}$ at
${\sim } 4\times 10^4\ \textrm {T}$ at ![]() $l=40\ \textrm {nm}$ around the laser spot). This field tends to deflect the hot electrons in the transverse direction, hence limiting the growth of the on-axis electrostatic sheath field (
$l=40\ \textrm {nm}$ around the laser spot). This field tends to deflect the hot electrons in the transverse direction, hence limiting the growth of the on-axis electrostatic sheath field (![]() $E_x$) already before the on-target pulse maximum. This is evidenced in figure 4(c), which plots, for both
$E_x$) already before the on-target pulse maximum. This is evidenced in figure 4(c), which plots, for both ![]() $l=20\ \textrm {nm}$ and 40 nm, the temporal evolution of the maximum value of
$l=20\ \textrm {nm}$ and 40 nm, the temporal evolution of the maximum value of ![]() $E_x$ on axis at the rear surface. A similar magnetic effect has previously been shown experimentally to inhibit TNSA in micrometric targets (Nakatsutsumi et al. Reference Nakatsutsumi, Sentoku, Korzhimanov, Chen, Buffechoux, Kon, Atherton, Audebert, Geissel and Hurd2018). Therefore, although they are expected to produce stronger sheath fields, the thicker targets that turn transparent at
$E_x$ on axis at the rear surface. A similar magnetic effect has previously been shown experimentally to inhibit TNSA in micrometric targets (Nakatsutsumi et al. Reference Nakatsutsumi, Sentoku, Korzhimanov, Chen, Buffechoux, Kon, Atherton, Audebert, Geissel and Hurd2018). Therefore, although they are expected to produce stronger sheath fields, the thicker targets that turn transparent at ![]() $\theta =45^\circ$ do not yield faster ions, ultimately resulting in an optimum target thickness that is approximately half that found at
$\theta =45^\circ$ do not yield faster ions, ultimately resulting in an optimum target thickness that is approximately half that found at ![]() $\theta =0^\circ$.
$\theta =0^\circ$.

Figure 4. (a,b) Magnetostatic ![]() $B_z$ field (in T)
$B_z$ field (in T) ![]() $10\ \textrm {fs}$ before the on-target laser peak for a single obliquely incident pulse and target thicknesses (a)
$10\ \textrm {fs}$ before the on-target laser peak for a single obliquely incident pulse and target thicknesses (a) ![]() $l=20\ \textrm {nm}$ and (b)
$l=20\ \textrm {nm}$ and (b) ![]() $l=40\ \textrm {nm}$. (c) Maximum of the ion-accelerating, electrostatic field
$l=40\ \textrm {nm}$. (c) Maximum of the ion-accelerating, electrostatic field ![]() $E_x$ on axis at the rear surface before the on-target peak, for foil thicknesses 20 nm (black) and 40 nm (red).
$E_x$ on axis at the rear surface before the on-target peak, for foil thicknesses 20 nm (black) and 40 nm (red).
3. Proton acceleration with colliding laser pulses in relativistically transparent foils
We now turn to a configuration where the main laser pulse (of total energy of 16 J) is split into two half-pulses of equal energy (8 J) incident on the target at opposite angles (![]() ${\pm }45^\circ$), similarly to the lower-intensity set-up that was lately found to boost TNSA (Ferri et al. Reference Ferri, Siminos and Fülöp2019). Such a configuration could be implemented at multiple-beam laser facilities, or at single-beam facilities using split-mirror set-ups enabling spatial and temporal separation of a laser pulse (Aurand et al. Reference Aurand, Hansson, Senje, Svensson, Persson, Neely, Lundh and Wahlström2015, Reference Aurand, Senje, Svensson, Hansson, Higginson, Gonoskov, Marklund, Persson, Lundh and Neely2016). In that case, to ensure overlap, the delay between the two pulses and the difference in their focus position should be small compared, respectively, with the laser duration and spot size. The other parameters remain the same as in the previous section.
${\pm }45^\circ$), similarly to the lower-intensity set-up that was lately found to boost TNSA (Ferri et al. Reference Ferri, Siminos and Fülöp2019). Such a configuration could be implemented at multiple-beam laser facilities, or at single-beam facilities using split-mirror set-ups enabling spatial and temporal separation of a laser pulse (Aurand et al. Reference Aurand, Hansson, Senje, Svensson, Persson, Neely, Lundh and Wahlström2015, Reference Aurand, Senje, Svensson, Hansson, Higginson, Gonoskov, Marklund, Persson, Lundh and Neely2016). In that case, to ensure overlap, the delay between the two pulses and the difference in their focus position should be small compared, respectively, with the laser duration and spot size. The other parameters remain the same as in the previous section.
The use of two half-pulses yields a larger optimal target thickness than with a single pulse, with best results obtained for ![]() $l=30\text {--}40\ \textrm {nm}$, both regarding the maximum energy (figure 5a) and number (figure 5b) of accelerated protons. In addition, the proton maximum energy is increased from 119 to 137 MeV. Remarkably, this enhancement goes along with a 3–4-fold rise in the number of high-energy (
$l=30\text {--}40\ \textrm {nm}$, both regarding the maximum energy (figure 5a) and number (figure 5b) of accelerated protons. In addition, the proton maximum energy is increased from 119 to 137 MeV. Remarkably, this enhancement goes along with a 3–4-fold rise in the number of high-energy (![]() ${>}30\ \textrm {MeV}$) protons. When compared with the reference case at normal incidence, the two-pulse set-up allows the maximum proton energy to be increased by
${>}30\ \textrm {MeV}$) protons. When compared with the reference case at normal incidence, the two-pulse set-up allows the maximum proton energy to be increased by ![]() ${>}30\,\%$, and the number of energetic protons to be multiplied by a factor of 4. Although the gain over the single obliquely incident pulse is less impressive, the predicted doubled optimal target thickness could ease the experimental investigation of ion acceleration from relativistically transparent solid foils, given the practical difficulties of manipulating such ultrathin targets. This applies, in particular, to modest-energy laser systems which may not allow RSIT to be achieved at handleable target thicknesses. Finally, figure 5(c) shows that the two-pulse scheme leads to substantial improvements in the proton energy spectra over the single-pulse case, both at normal and oblique incidence.
${>}30\,\%$, and the number of energetic protons to be multiplied by a factor of 4. Although the gain over the single obliquely incident pulse is less impressive, the predicted doubled optimal target thickness could ease the experimental investigation of ion acceleration from relativistically transparent solid foils, given the practical difficulties of manipulating such ultrathin targets. This applies, in particular, to modest-energy laser systems which may not allow RSIT to be achieved at handleable target thicknesses. Finally, figure 5(c) shows that the two-pulse scheme leads to substantial improvements in the proton energy spectra over the single-pulse case, both at normal and oblique incidence.

Figure 5. (a,b) Ion acceleration by two ![]() $8\ \textrm {J}$,
$8\ \textrm {J}$, ![]() $38\ \textrm {fs}$ half-pulses incident at
$38\ \textrm {fs}$ half-pulses incident at ![]() ${\pm }45^\circ$ angles (dashed red) as a function of the
${\pm }45^\circ$ angles (dashed red) as a function of the ![]() $\textrm {CH}_2$ foil thickness, compared to the results obtained with a single, obliquely incident
$\textrm {CH}_2$ foil thickness, compared to the results obtained with a single, obliquely incident ![]() $16\ \textrm {J}$ pulse (solid blue): (a) maximum proton energy and (b) number of protons with
$16\ \textrm {J}$ pulse (solid blue): (a) maximum proton energy and (b) number of protons with ![]() ${>}30\ \textrm {MeV}$ energies. (c) Proton energy distributions from a
${>}30\ \textrm {MeV}$ energies. (c) Proton energy distributions from a ![]() $40\ \textrm {nm}$ foil using two half-pulses (red), or a single pulse at normal (black) and oblique (blue) incidence. Solid (respectively dashed) curves correspond to
$40\ \textrm {nm}$ foil using two half-pulses (red), or a single pulse at normal (black) and oblique (blue) incidence. Solid (respectively dashed) curves correspond to ![]() $l=40\ \textrm {nm}$ (respectively 20 nm).
$l=40\ \textrm {nm}$ (respectively 20 nm).
In the two-pulse scheme, the irradiated plasma area is comparable to that associated with a single pulse at oblique incidence. The larger optimum thickness and enhanced ion acceleration then mainly result from the modified electron dynamics in the two-pulse field distribution, as has been described earlier in the TNSA regime (Ferri et al. Reference Ferri, Siminos and Fülöp2019). For a given target thickness, owing to the stronger electron heating, transparency is then more easily induced using two half-pulses. This is clearly shown in figure 6, with a transmission coefficient rising from ![]() $C_T=0.21$ to
$C_T=0.21$ to ![]() $C_T=0.38$ between the single- and two-pulse cases. By examining the laser field distributions in both configurations at various successive times, we checked that RSIT occurs earlier in time using two half-pulses, a result consistent with the
$C_T=0.38$ between the single- and two-pulse cases. By examining the laser field distributions in both configurations at various successive times, we checked that RSIT occurs earlier in time using two half-pulses, a result consistent with the ![]() ${\sim }25\,\%$ increase in the absorption coefficient.
${\sim }25\,\%$ increase in the absorption coefficient.

Figure 6. (a,b) Transverse electric field ![]() $E_y$ (in
$E_y$ (in ![]() $\textrm {V}\,\textrm {m}^{-1}$)
$\textrm {V}\,\textrm {m}^{-1}$) ![]() $35\ \textrm {fs}$ after the on-target laser peak for a single obliquely incident pulse (a) and two half-pulses (b) of same (
$35\ \textrm {fs}$ after the on-target laser peak for a single obliquely incident pulse (a) and two half-pulses (b) of same (![]() $16\ \textrm {J}$) total energy. In both cases, the target thickness is set to
$16\ \textrm {J}$) total energy. In both cases, the target thickness is set to ![]() $40\ \textrm {nm}$, and the measured values of the reflection (
$40\ \textrm {nm}$, and the measured values of the reflection (![]() $C_R$), transmission (
$C_R$), transmission (![]() $C_T$) and absorption (
$C_T$) and absorption (![]() $C_A$) coefficients are indicated. The dashed black line delineates the initial position of the target, while the thin grey line serves to highlight that RSIT sets in earlier in (b) than in (a). (c) Electron energy distribution at the peak laser intensity and (d) time evolution of the relativistic skin depth
$C_A$) coefficients are indicated. The dashed black line delineates the initial position of the target, while the thin grey line serves to highlight that RSIT sets in earlier in (b) than in (a). (c) Electron energy distribution at the peak laser intensity and (d) time evolution of the relativistic skin depth ![]() $l_s=\sqrt {\langle \gamma \rangle } c/\omega _p$ (with
$l_s=\sqrt {\langle \gamma \rangle } c/\omega _p$ (with ![]() $\langle \gamma \rangle$ the averaged electron Lorentz factor over the laser spot) using a single (blue) or two (red) pulses. The dashed black line indicates the time of the on-target intensity peak. The solid black line indicates the initial target thickness (40 nm).
$\langle \gamma \rangle$ the averaged electron Lorentz factor over the laser spot) using a single (blue) or two (red) pulses. The dashed black line indicates the time of the on-target intensity peak. The solid black line indicates the initial target thickness (40 nm).
The stronger electron heating (see figure 6c) that accounts for the enhanced laser absorption facilitates the induction of transparency. Figure 6(d) shows the temporal evolution of the relativistic skin depth ![]() $l_s=\sqrt {\langle \gamma \rangle } c/\omega _p$ during the interaction, with
$l_s=\sqrt {\langle \gamma \rangle } c/\omega _p$ during the interaction, with ![]() $\omega _p$ the plasma frequency and
$\omega _p$ the plasma frequency and ![]() $\langle \gamma \rangle$ the electron Lorentz factor spatially averaged over the target thickness and around the laser spot. As expected, the use of the two half-pulses causes a faster increase in
$\langle \gamma \rangle$ the electron Lorentz factor spatially averaged over the target thickness and around the laser spot. As expected, the use of the two half-pulses causes a faster increase in ![]() $l_s$ with the laser intensity. We can consider that RSIT sets in when
$l_s$ with the laser intensity. We can consider that RSIT sets in when ![]() $l_s$ becomes higher than the initial target thickness (
$l_s$ becomes higher than the initial target thickness (![]() $l=40\ \textrm {nm}$) even if this is a simplified approach as
$l=40\ \textrm {nm}$) even if this is a simplified approach as ![]() $l_s$ cannot entirely describe RSIT in such overdense plasmas (Cattani et al. Reference Cattani, Kim, Anderson and Lisak2000). In the two-pulse case, this criterion is fulfilled approximately 10–15 fs prior to the laser peak time, which incidentally coincides with the onset of RSIT with a single pulse. This delay between the onset times of RSIT using one or two pulses appears to be consistent with the difference between the transmitted fractions of the laser field in figure 6.
$l_s$ cannot entirely describe RSIT in such overdense plasmas (Cattani et al. Reference Cattani, Kim, Anderson and Lisak2000). In the two-pulse case, this criterion is fulfilled approximately 10–15 fs prior to the laser peak time, which incidentally coincides with the onset of RSIT with a single pulse. This delay between the onset times of RSIT using one or two pulses appears to be consistent with the difference between the transmitted fractions of the laser field in figure 6.
Furthermore, the symmetry (relative to the ![]() $x$ axis) of the two-pulse set-up prevents the development of a strong surface magnetostatic field. Figure 7 shows this field 10 fs before the on-target laser peak for a 40 nm thick target. As expected from the symmetry of the problem, the
$x$ axis) of the two-pulse set-up prevents the development of a strong surface magnetostatic field. Figure 7 shows this field 10 fs before the on-target laser peak for a 40 nm thick target. As expected from the symmetry of the problem, the ![]() $B_z$ field vanishes on axis, and thus cannot counteract the sheath-field-enhancing effect of the stronger laser absorption.
$B_z$ field vanishes on axis, and thus cannot counteract the sheath-field-enhancing effect of the stronger laser absorption.

Figure 7. Quasistatic ![]() $B_z$ field (in T) 10 fs before the on-target intensity peak for two half-pulses interacting with a 40 nm foil.
$B_z$ field (in T) 10 fs before the on-target intensity peak for two half-pulses interacting with a 40 nm foil.
4. Conclusions
Using 2-D PIC simulations, we have examined the efficiency of laser-driven proton acceleration in relativistically transparent, ultrathin ![]() $\textrm {CH}_2$ foil targets under different short-pulse irradiation conditions. As baseline laser parameters, we have considered a
$\textrm {CH}_2$ foil targets under different short-pulse irradiation conditions. As baseline laser parameters, we have considered a ![]() $5\times 10^{20}\ \textrm {W}\,\textrm {cm}^{-2}$ maximum intensity and a 38 fs pulse duration. First, we have showed that operating at oblique incidence can be beneficial to proton acceleration, owing to enhanced energy absorption into hot electrons. Yet, the optimum target thickness (
$5\times 10^{20}\ \textrm {W}\,\textrm {cm}^{-2}$ maximum intensity and a 38 fs pulse duration. First, we have showed that operating at oblique incidence can be beneficial to proton acceleration, owing to enhanced energy absorption into hot electrons. Yet, the optimum target thickness (![]() $l\simeq 20\ \textrm {nm}$) is then reduced compared to that found at normal incidence (
$l\simeq 20\ \textrm {nm}$) is then reduced compared to that found at normal incidence (![]() $l \simeq 40\ \textrm {nm}$), as a result of strong (
$l \simeq 40\ \textrm {nm}$), as a result of strong (![]() ${>}10^4\ \textrm {T}$) surface magnetostatic fields self-induced within the ion acceleration region. In a second step, we have studied a configuration in which the laser pulse is split into two half-pulses with the same total energy, incoming simultaneously on target but with opposite angles of incidence. This configuration enhances the electron heating while preventing the buildup of deleterious surface
${>}10^4\ \textrm {T}$) surface magnetostatic fields self-induced within the ion acceleration region. In a second step, we have studied a configuration in which the laser pulse is split into two half-pulses with the same total energy, incoming simultaneously on target but with opposite angles of incidence. This configuration enhances the electron heating while preventing the buildup of deleterious surface ![]() $B$-fields within the laser spot. Not only does it allow one to use thicker targets than with a single obliquely incident pulse, but it also yields substantial increases in the proton numbers (
$B$-fields within the laser spot. Not only does it allow one to use thicker targets than with a single obliquely incident pulse, but it also yields substantial increases in the proton numbers (![]() $\times 4$) and cutoff energies (
$\times 4$) and cutoff energies (![]() ${\times }1.3$) over the baseline set-up. Our study suggests that the constraints posed by nanometric targets in experiments on RSIT could be somewhat relaxed using a two-pulse scheme.
${\times }1.3$) over the baseline set-up. Our study suggests that the constraints posed by nanometric targets in experiments on RSIT could be somewhat relaxed using a two-pulse scheme.
Acknowledgements
The authors would like to acknowledge fruitful discussions with I. Thiele and L. Yi. This work was supported by the Knut and Alice Wallenberg Foundation, the Swedish Research Council, Grant No. 2016-05012, and has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme under grant agreement No 647121. The simulations were performed on resources at Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC).
Editor Luis Silva thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.