Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T10:04:23.963Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTINUOUS QUIVERS OF TYPE A (III) EMBEDDINGS OF CLUSTER THEORIES

Part of: Arithmetic rings and other special rings Representation theory of rings and algebras

Published online by Cambridge University Press:  11 February 2022

KIYOSHI IGUSA Open the ORCID record for KIYOSHI IGUSA [Opens in a new window] ,
JOB D. ROCK Open the ORCID record for JOB D. ROCK [Opens in a new window]  and
GORDANA TODOROV Open the ORCID record for GORDANA TODOROV [Opens in a new window]
KIYOSHI IGUSA
Affiliation:
Mathematics Department Brandeis University Waltham, Massachusetts 02453, USA igusa@brandeis.edu
JOB D. ROCK
Affiliation:
Hausdorff Research Institute for Mathematics Poppelsdorfer Alle 45 Bonn 53115, Germany jobrock@brandeis.edu
GORDANA TODOROV
Affiliation:
Mathematics Department Northeastern University Boston, Massachusetts 02115, USA g.todorov@northeastern.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We continue the work started in parts (I) and (II) of this series. In this paper, we classify which continuous quivers of type A are derived equivalent. Next, we define the new 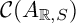${\mathcal {C}(A_{{\mathbb {R}},S})}$ , which we call weak continuous cluster category. It is a triangulated category, it does not have cluster structure but it has a new weaker notion of “cluster theory.” We show that the original continuous cluster category of [15] is a localization of this new weak continuous cluster category. We define cluster theories to be appropriate groupoids and we show that cluster structures satisfy the conditions for cluster theories. We describe the relationship between different cluster theories: some new and some obtained from cluster structures. The notion of continuous mutation which appears in cluster theories (but not in cluster structures) appears in the next paper [20].

MSC classification

Primary: 13F60: Cluster algebras
Secondary: 16G20: Representations of quivers and partially ordered sets
Type
Article
Information
Nagoya Mathematical Journal , Volume 247 , September 2022 , pp. 653 - 689
Check for updates
Copyright
© (2022) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by supported by Simons Foundation.

References

Baur, K. and Graz, S., Transfinite mutations in the completed infinity-gon , J. Combin. Theory Ser. A 155 (2018), 321–359. doi:10.1016/j.jcta.2017.11.011. Google Scholar
Botnan, M. B. and Crawley-Boevey, W., Decomposition of persistence modules , Proc. Amer. Math. Soc. 148 (2020), 4581–4596. doi:10.1090/proc/14790. CrossRefGoogle Scholar
Buan, A., Iyama, O., Reiten, I., and Scott, J., Cluster structures for 2-Calabi–Yau categories and unipotent groups . Compos. Math. 145 (2009), no. 4, 1035–1079.CrossRefGoogle Scholar
Buan, A., Marsh, B., Reineke, M., Reiten, I., and Todorov, G., Tilting theory and cluster combinatorics , Adv. Math. 204 (2006), no. 2, 572–618. doi:10.1016/j.aim.2005.06.003. CrossRefGoogle Scholar
Caldero, P., Chapoton, F., and Schiffler, R., Quivers with relations arising from clusters $({A}_n$ Case), Trans. Amer. Math. Soc. 358 (2006), no. 3, 1347–1364. doi:10.1090/S0002-9947-05-03753-0. CrossRefGoogle Scholar
Fomin, S. and Zelevinksy, A., Cluter algebras I: Foundations , J. Amer. Math. Soc. 15 (2002), no. 2, 497–529. doi:10.1090/S0894-0347-01-00385-X. Google Scholar
Fomin, S. and Zelevinksy, A., Cluster algebras II: Finite type classification , Invent. Math. 154 (2002), no. 1, 63–121. doi:10.1007/s00222-003-0302-y. CrossRefGoogle Scholar
Fomin, S. and Zelevinksy, A., Cluster algebras III: Upper bounds and double Bruhat cells , Duke Math. J. 126 (2005), no. 1, 1–52. doi:10.1215/S0012-7094-04-12611-9. Google Scholar
Fomin, S. and Zelevinksy, A., Cluster algebras IV: Coefficients , Compos. Math. 143 (2007), no. 1, 112–164. doi:10.1112/S0010437X06002521. CrossRefGoogle Scholar
Garcia, M. and Igusa, K., Continuously triangulating the continuous cluster category , Topology Appl. 285 (2020), 107411. doi:10.1016/j.topol.2020.107411. CrossRefGoogle Scholar
Happel, D., Triangulated Categories in the Representation Theory of Finite Dimensional Algebras, London Math. Soc. Lecture Note Ser. 119, Cambridge University Press, 1988, New York, NY, USA. doi:10.1017/CBO9780511629228.CrossRefGoogle Scholar
Holm, T. and Jørgensen, P., On a cluster category of infinite Dynkin type, and the relation to triangulations of the infinity-gon , Math. Z. 270 (2012), no. 1, 277–295. doi:10.1007/s00209-010-0797-z. Google Scholar
Holm, T. and Jørgensen, P., Cluster tilting vs. weak cluster tilting in Dynkin type A infinity , Forum Math. 27 (2015), no. 2, 1117–1137,CrossRefGoogle Scholar
Igusa, K., Rock, J. D., and Todorov, G., Continuous Quivers of Type A (I) Foundations, Rendiconti del Circolo Matematico di Palermo Series 2 (2022), https://doi.org/10.1007/s12215-021-00691-x.CrossRefGoogle Scholar
Igusa, K. and Todorov, G., Continuous cluster categories I , Algebr. Represent. Theory 18 (2015), no. 1, 65–101. doi:10.1007/s10468-014-9481-z. CrossRefGoogle Scholar
Jørgensen, P. and Yakimov, M., $c$ -vectors of 2-Calabi–Yau categories and Borel subalgebras of ${\mathrm{sl}}_{\infty }$ , Selecta Math. (N.S.) 26 (2020), no. 1, 1–46. doi:10.1007/s00029-019-0525-4. CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Categories and Sheaves, Grundlehren Math. Wiss. 60 (2008), no. 2, 217–221. doi:10.11429/sugaku.0602217 Google Scholar
Neeman, A., Triangulated Categories, Ann. Math. Stud. 148, Princeton University Press, 2001, Princeton, NJ, USA.CrossRefGoogle Scholar
Rock, J. D., Continuous quivers of type $\mathrm{A}$ (II) the Auslander–Reiten space, preprint, 2020. arXiv:1910.04140v2 [math.RT].Google Scholar
Rock, J. D., Continuous quivers of type $A$ (IV) continuous mutation and geometric models of E-clusters, preprint, 2020. arXiv:2004.11341v1 [math.RT].Google Scholar