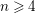1 Overview
The braid groups ![]() $B_{n}$ were introduced in the 1930s in the work of Artin [Reference Artin2]. An element
$B_{n}$ were introduced in the 1930s in the work of Artin [Reference Artin2]. An element ![]() $b\in B_{n}$ is called an
$b\in B_{n}$ is called an ![]() $n$-braid. Alexander [Reference Alexander1] related braids to knots and links in real 3-dimensional space, by means of a closure operation
$n$-braid. Alexander [Reference Alexander1] related braids to knots and links in real 3-dimensional space, by means of a closure operation ![]() $\hat{~}$. In that realm, it became important to understand the braid representatives of a given link
$\hat{~}$. In that realm, it became important to understand the braid representatives of a given link ![]() $L$, that is, those
$L$, that is, those ![]() $b$ with
$b$ with ![]() $L=\hat{b}$. Markov’s theorem relates these representatives by two moves, the conjugacy in the braid group, and (de)stabilization, which passes between
$L=\hat{b}$. Markov’s theorem relates these representatives by two moves, the conjugacy in the braid group, and (de)stabilization, which passes between ![]() $b\in B_{n}$ and
$b\in B_{n}$ and ![]() $b\unicode[STIX]{x1D70E}_{n}^{\pm 1}\in B_{n+1}$ (see, e.g., [Reference Morton14]). Markov’s moves and braid group algebra have become fundamental in Jones’ pioneering work [Reference Jones11] and its later continuation toward quantum invariants. Conjugacy is, starting with Garside’s [Reference Garside9], and later many others’ work, now relatively well group-theoretically understood. In contrast, the effect of (de)stabilization on conjugacy classes of braid representatives of a given link is in general difficult to understand. Only in very special situations can these conjugacy classes be well described, for example, [Reference Birman and Menasco5].
$b\unicode[STIX]{x1D70E}_{n}^{\pm 1}\in B_{n+1}$ (see, e.g., [Reference Morton14]). Markov’s moves and braid group algebra have become fundamental in Jones’ pioneering work [Reference Jones11] and its later continuation toward quantum invariants. Conjugacy is, starting with Garside’s [Reference Garside9], and later many others’ work, now relatively well group-theoretically understood. In contrast, the effect of (de)stabilization on conjugacy classes of braid representatives of a given link is in general difficult to understand. Only in very special situations can these conjugacy classes be well described, for example, [Reference Birman and Menasco5].
In this paper we are concerned with the question when infinitely many conjugacy classes of ![]() $n$-braid representatives of a given knot occur. Birman and Menasco [Reference Birman and Menasco4] introduced a move called exchange move (see Section 2.2), and proved that it necessarily underlies the switch between many conjugacy classes of braid representatives of
$n$-braid representatives of a given knot occur. Birman and Menasco [Reference Birman and Menasco4] introduced a move called exchange move (see Section 2.2), and proved that it necessarily underlies the switch between many conjugacy classes of braid representatives of ![]() $L$. We prove here that it is also sufficient for generating infinitely many such classes.
$L$. We prove here that it is also sufficient for generating infinitely many such classes.
Theorem 1.1. Let ![]() $K$ be a knot and
$K$ be a knot and ![]() $n\geqslant 4$. Then
$n\geqslant 4$. Then ![]() $K$ has infinitely many conjugacy classes of
$K$ has infinitely many conjugacy classes of ![]() $n$-braid representatives if and only if it has one admitting an exchange move.
$n$-braid representatives if and only if it has one admitting an exchange move.
Among the different braid representatives of a link ![]() $L$ the one with the fewest strands is called a minimal braid. The number of strands of a minimal braid is called the braid index
$L$ the one with the fewest strands is called a minimal braid. The number of strands of a minimal braid is called the braid index ![]() $b(L)$ of
$b(L)$ of ![]() $L$. Obviously it makes sense to consider only
$L$. Obviously it makes sense to consider only ![]() $n\geqslant b(L)$.
$n\geqslant b(L)$.
Some nonconjugate braids close to isotopic links. Birman had observed [Reference Birman3] that stabilizations of different signs are nonconjugate, because of different exponent sum. However, it is well known now that for any link ![]() $L$ and
$L$ and ![]() $n\geqslant b(L)$, there are only finitely many exponent sums of
$n\geqslant b(L)$, there are only finitely many exponent sums of ![]() $n$-braid representatives of
$n$-braid representatives of ![]() $L$. This is a consequence of Birman–Menasco’s Theorem 2.1 stated below, but also, much more directly, of the Morton–Franks–Williams inequality for the skein polynomial. Therefore, the exponent sum is (not very surprisingly) too weak to distinguish infinitely many conjugacy classes. It was also known from [Reference Birman and Menasco5] that only finitely many conjugacy classes occur when
$L$. This is a consequence of Birman–Menasco’s Theorem 2.1 stated below, but also, much more directly, of the Morton–Franks–Williams inequality for the skein polynomial. Therefore, the exponent sum is (not very surprisingly) too weak to distinguish infinitely many conjugacy classes. It was also known from [Reference Birman and Menasco5] that only finitely many conjugacy classes occur when ![]() $n\leqslant 3$.
$n\leqslant 3$.
In the case ![]() $n>b(L)$ of nonminimal braids, Morton [Reference Morton13] discovered an infinite sequence of conjugacy classes of 4-braids with closure being the unknot. Further examples were exhibited more recently by Fukunaga [Reference Fukunaga7, Reference Fukunaga8] and Shinjo [Reference Shinjo18]. For every knot, there are obvious (stabilized) nonminimal braid representatives admitting an exchange move. Thus Theorem 1.1 can always be applied. Shinjo obtained this special case of the theorem in her previous paper [Reference Shinjo19].
$n>b(L)$ of nonminimal braids, Morton [Reference Morton13] discovered an infinite sequence of conjugacy classes of 4-braids with closure being the unknot. Further examples were exhibited more recently by Fukunaga [Reference Fukunaga7, Reference Fukunaga8] and Shinjo [Reference Shinjo18]. For every knot, there are obvious (stabilized) nonminimal braid representatives admitting an exchange move. Thus Theorem 1.1 can always be applied. Shinjo obtained this special case of the theorem in her previous paper [Reference Shinjo19].
In the case ![]() $n=b(L)$ of minimal braids, Birman had conjectured that there would always be a single conjugacy class of minimal braids representing a link. However, Murasugi and Thomas [Reference Murasugi and Thomas16] disproved Birman’s conjecture, exhibiting some counterexamples inFootnote 1
$n=b(L)$ of minimal braids, Birman had conjectured that there would always be a single conjugacy class of minimal braids representing a link. However, Murasugi and Thomas [Reference Murasugi and Thomas16] disproved Birman’s conjecture, exhibiting some counterexamples inFootnote 1 ![]() $B_{4}$. Our result can be seen, for knots, as such a general construction. It is also a precursor to a follow-up paper [Reference Shinjo and Stoimenow20], where we discuss in more detail the case of links (for which also special cases were known [Reference Stoimenow21, Reference Stoimenow22]), and extend our main result.
$B_{4}$. Our result can be seen, for knots, as such a general construction. It is also a precursor to a follow-up paper [Reference Shinjo and Stoimenow20], where we discuss in more detail the case of links (for which also special cases were known [Reference Stoimenow21, Reference Stoimenow22]), and extend our main result.
2 Preliminaries
2.1 Braids and closures
Definition 1. The braid group ![]() $B_{n}$ on
$B_{n}$ on ![]() $n$ strands can be defined by generators and relations as
$n$ strands can be defined by generators and relations as
The ![]() $\unicode[STIX]{x1D70E}_{i}$ are called Artin standard generators. An element
$\unicode[STIX]{x1D70E}_{i}$ are called Artin standard generators. An element ![]() $b\in B_{n}$ is an
$b\in B_{n}$ is an ![]() $n$-braid.
$n$-braid.
There is a graphical representative of braids, where in ![]() $\unicode[STIX]{x1D70E}_{i}$ strands
$\unicode[STIX]{x1D70E}_{i}$ strands ![]() $i$ and
$i$ and ![]() $i+1$ cross, and multiplication is given by stacking. (We number strands from left to right and orient them downward.)
$i+1$ cross, and multiplication is given by stacking. (We number strands from left to right and orient them downward.)

The closure ![]() $\hat{b}$ of a braid
$\hat{b}$ of a braid ![]() $b$ is a knot or link (with orientation) in
$b$ is a knot or link (with orientation) in ![]() $S^{3}$:
$S^{3}$:

There is a permutation homomorphism of ![]() $B_{n}$,
$B_{n}$,
(The permutation on the right is a transposition.) We call ![]() $\unicode[STIX]{x1D70B}(b)$ the braid permutation of
$\unicode[STIX]{x1D70B}(b)$ the braid permutation of ![]() $b$. We call
$b$. We call ![]() $b$ a pure braid if
$b$ a pure braid if ![]() $\unicode[STIX]{x1D70B}(b)=Id$.
$\unicode[STIX]{x1D70B}(b)=Id$.
Let ![]() $b$ be an
$b$ be an ![]() $n$-braid with numbered endpoints as in Figure 1. Suppose that
$n$-braid with numbered endpoints as in Figure 1. Suppose that ![]() $b$ has its strings connected as follows:
$b$ has its strings connected as follows: ![]() $1$ to
$1$ to ![]() $i_{1}$,
$i_{1}$, ![]() $2$ to
$2$ to ![]() $i_{2},\ldots ,n$ to
$i_{2},\ldots ,n$ to ![]() $i_{n}$, that is,
$i_{n}$, that is, ![]() $\unicode[STIX]{x1D70B}(b)(k)=i_{k}$. Then we write
$\unicode[STIX]{x1D70B}(b)(k)=i_{k}$. Then we write
For example the braid ![]() $b_{1}$ in Figure 1 has the permutation
$b_{1}$ in Figure 1 has the permutation
where ![]() $(1~2~4~3)$ means a cyclic permutation. The braid
$(1~2~4~3)$ means a cyclic permutation. The braid ![]() $b_{2}$ in the figure has the permutation
$b_{2}$ in the figure has the permutation ![]() $(1~3~5)(2~4)$. We remark that when the closure of
$(1~3~5)(2~4)$. We remark that when the closure of ![]() $b$ is a
$b$ is a ![]() $k$-component link, the braid permutation of
$k$-component link, the braid permutation of ![]() $b$ is a product of
$b$ is a product of ![]() $k$ disjoint cycles. (We will be mainly interested in
$k$ disjoint cycles. (We will be mainly interested in ![]() $k=1$.) The length of each cycle is equal to the number of strings of
$k=1$.) The length of each cycle is equal to the number of strings of ![]() $b$ which make up a component of
$b$ which make up a component of ![]() $\hat{b}$.
$\hat{b}$.
When we choose a (nonempty) subset ![]() $C$ of
$C$ of ![]() $\{1,\ldots ,n\}$ whose elements form a subset of the cycles of
$\{1,\ldots ,n\}$ whose elements form a subset of the cycles of ![]() $\unicode[STIX]{x1D70B}(b)$, we can define a subbraid
$\unicode[STIX]{x1D70B}(b)$, we can define a subbraid ![]() $b^{\prime }$ of
$b^{\prime }$ of ![]() $b$ by choosing only strings numbered in
$b$ by choosing only strings numbered in ![]() $C$. For subbraids
$C$. For subbraids ![]() $b^{\prime }$ and
$b^{\prime }$ and ![]() $b^{\prime \prime }$ of
$b^{\prime \prime }$ of ![]() $b$ one can define the (strand) linking number
$b$ one can define the (strand) linking number ![]() $lk(b^{\prime },b^{\prime \prime })$ by the linking number
$lk(b^{\prime },b^{\prime \prime })$ by the linking number ![]() $lk(\hat{b}^{\prime },\hat{b}^{\prime \prime })$ between sublinks of
$lk(\hat{b}^{\prime },\hat{b}^{\prime \prime })$ between sublinks of ![]() $\hat{b}$. For example, in
$\hat{b}$. For example, in ![]() $b_{2}$ of Figure 1, we have
$b_{2}$ of Figure 1, we have ![]() $lk(b_{2}^{\prime },b_{2}^{\prime \prime })=0$, where
$lk(b_{2}^{\prime },b_{2}^{\prime \prime })=0$, where ![]() $\hat{b}_{2}^{\prime }$ and
$\hat{b}_{2}^{\prime }$ and ![]() $\hat{b}_{2}^{\prime \prime }$ are the two components of
$\hat{b}_{2}^{\prime \prime }$ are the two components of ![]() $\hat{b}_{2}$. (The subbraid
$\hat{b}_{2}$. (The subbraid ![]() $b_{2}^{\prime }$ comprises the strings starting at the top as number
$b_{2}^{\prime }$ comprises the strings starting at the top as number ![]() $1,3,5$, and
$1,3,5$, and ![]() $b_{2}^{\prime \prime }$ strings
$b_{2}^{\prime \prime }$ strings ![]() $2,4$.)
$2,4$.)

Figure 1. An ![]() $n$-braid.
$n$-braid.
2.2 Exchange moves
Let
be the (right-handed) full twist on ![]() $n$ strands. The center of
$n$ strands. The center of ![]() $B_{n}$ (elements that commute with all
$B_{n}$ (elements that commute with all ![]() $B_{n}$) is infinite cyclic and generated by
$B_{n}$) is infinite cyclic and generated by ![]() $\unicode[STIX]{x1D6E5}_{n}^{2}$. Let similarly
$\unicode[STIX]{x1D6E5}_{n}^{2}$. Let similarly
be the restricted full twist on strands ![]() $i$ to
$i$ to ![]() $j$. Let also for
$j$. Let also for ![]() $1\leqslant i<j\leqslant n$,
$1\leqslant i<j\leqslant n$,
be the subgroup of ![]() $B_{n}$ of braids operating on strands
$B_{n}$ of braids operating on strands ![]() $i\,\ldots ,j$. Where ambiguity is avoided (as indicated by diagrams we draw), we can identify
$i\,\ldots ,j$. Where ambiguity is avoided (as indicated by diagrams we draw), we can identify ![]() $B_{i,j}\simeq B_{j-i+1}$.
$B_{i,j}\simeq B_{j-i+1}$.
We say that ![]() $b\in B_{n}$admits an exchange move, if
$b\in B_{n}$admits an exchange move, if ![]() $b$ is as illustrated in Figure 2, where
$b$ is as illustrated in Figure 2, where ![]() $\unicode[STIX]{x1D6FC}\in B_{1,n-1}$,
$\unicode[STIX]{x1D6FC}\in B_{1,n-1}$, ![]() $\unicode[STIX]{x1D6FD}\in B_{2,n}$, and
$\unicode[STIX]{x1D6FD}\in B_{2,n}$, and ![]() $n\geqslant 4$.
$n\geqslant 4$.

Figure 2. The ![]() $n$-braid
$n$-braid ![]() $b$.
$b$.
An exchange move [Reference Birman and Menasco4] is the transformation between the braids ![]() $b$ and
$b$ and ![]() $b_{m}$ shown in Figure 3. Here
$b_{m}$ shown in Figure 3. Here ![]() $m$ is some nonzero integer, and the boxes labeled
$m$ is some nonzero integer, and the boxes labeled ![]() $\pm m$ represent the full twists
$\pm m$ represent the full twists ![]() $\unicode[STIX]{x1D6E5}_{[2,n-1]}^{\pm 2m}$ respectively, acting on the middle
$\unicode[STIX]{x1D6E5}_{[2,n-1]}^{\pm 2m}$ respectively, acting on the middle ![]() $n-2$ strands. (Thus a positive number of full twists are understood to be right full twists, and
$n-2$ strands. (Thus a positive number of full twists are understood to be right full twists, and ![]() $-m$ full twists mean
$-m$ full twists mean ![]() $m$ full left-handed twists.)
$m$ full left-handed twists.)

Figure 3. The braid ![]() $b_{m}$.
$b_{m}$.
Of course, no nontrivial braid on ![]() $2$ strands admits an exchange move, and all exchange moves on
$2$ strands admits an exchange move, and all exchange moves on ![]() $3$ strands are trivial, so that we naturally assume
$3$ strands are trivial, so that we naturally assume ![]() $n\geqslant 4$ throughout. There is another, more common, way to describe the exchange move, namely by
$n\geqslant 4$ throughout. There is another, more common, way to describe the exchange move, namely by
This description is equivalent to the previous one, because ![]() $\unicode[STIX]{x1D705}\cdot \unicode[STIX]{x1D6E5}_{[2,n-1]}^{2}=\unicode[STIX]{x1D6E5}_{[1,n-1]}^{2}$, and this element commutes with
$\unicode[STIX]{x1D705}\cdot \unicode[STIX]{x1D6E5}_{[2,n-1]}^{2}=\unicode[STIX]{x1D6E5}_{[1,n-1]}^{2}$, and this element commutes with ![]() $\unicode[STIX]{x1D6FC}$. A further equivalent formulation of the move, for
$\unicode[STIX]{x1D6FC}$. A further equivalent formulation of the move, for ![]() $m=\pm 1$, is
$m=\pm 1$, is
with ![]() $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }\in B_{2,n}$. This form is less convenient for out treatment, so we will not use it below.
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }\in B_{2,n}$. This form is less convenient for out treatment, so we will not use it below.
The exchange move underlies the switch between conjugacy classes with the same closure link, in a universal way.
Theorem 2.1. (Birman–Menasco [Reference Birman and Menasco4])
The ![]() $n$-braid representatives of a given link decompose into a finite number of classes under the combination of exchange moves and conjugacy.
$n$-braid representatives of a given link decompose into a finite number of classes under the combination of exchange moves and conjugacy.
2.3 Axis link and Conway polynomial
Definition 2. The axis (addition) link of a braid ![]() $b$, denoted by
$b$, denoted by ![]() $L_{b}$, is the oriented link consisting of the closure of
$L_{b}$, is the oriented link consisting of the closure of ![]() $b$ and an unknotted curve
$b$ and an unknotted curve ![]() $k$, the axis of the closed braid, as in Figure 4.
$k$, the axis of the closed braid, as in Figure 4.

Figure 4. The axis-addition link of ![]() $b$.
$b$.
We remark that the axis-addition links of conjugate braids are ambient isotopic. Thus for a proof of nonconjugacy we study invariants of the axis link. As such an invariant we employ the Conway polynomial ![]() $\unicode[STIX]{x1D6FB}$. It takes values in
$\unicode[STIX]{x1D6FB}$. It takes values in ![]() $\mathbb{Z}[z]$ and is given by the value
$\mathbb{Z}[z]$ and is given by the value ![]() $1$ on the unknot and the relation
$1$ on the unknot and the relation
This relation involves three links with diagrams

differing just at one crossing. They are called a skein triple. We write ![]() $[P]_{m}$ for the coefficient of
$[P]_{m}$ for the coefficient of ![]() $z^{m}$ in
$z^{m}$ in ![]() $P\in \mathbb{Z}[z]$, and more shortly
$P\in \mathbb{Z}[z]$, and more shortly ![]() $a_{m}=[\unicode[STIX]{x1D6FB}]_{m}$ for the coefficient of
$a_{m}=[\unicode[STIX]{x1D6FB}]_{m}$ for the coefficient of ![]() $z^{m}$ in the Conway polynomial. It is well known that for an
$z^{m}$ in the Conway polynomial. It is well known that for an ![]() $n$-component link
$n$-component link ![]() $L$, all coefficients of
$L$, all coefficients of ![]() $\unicode[STIX]{x1D6FB}$ in
$\unicode[STIX]{x1D6FB}$ in ![]() $z$-degree
$z$-degree ![]() $m$ vanish when
$m$ vanish when ![]() $m<n-1$ or
$m<n-1$ or ![]() $m+n$ is even.
$m+n$ is even.
We denote the linking number of two components of ![]() $L$ by
$L$ by ![]() $lk(\cdot ,\cdot )$. Now we recall a formula, given by Hoste [Reference Hoste10], which expresses the lowest nontrivial coefficient
$lk(\cdot ,\cdot )$. Now we recall a formula, given by Hoste [Reference Hoste10], which expresses the lowest nontrivial coefficient ![]() $a_{n-1}$ of
$a_{n-1}$ of ![]() $\unicode[STIX]{x1D6FB}(L)$ in terms of component linking numbers.
$\unicode[STIX]{x1D6FB}(L)$ in terms of component linking numbers.
Theorem 2.2. (see [Reference Hoste10])
Let ![]() $L=L_{1}\cup \cdots \cup L_{p}$ be a
$L=L_{1}\cup \cdots \cup L_{p}$ be a ![]() $p$-component link of components
$p$-component link of components ![]() $L_{1},\ldots ,L_{p}$. Let
$L_{1},\ldots ,L_{p}$. Let ![]() $l_{k,m}=lk(L_{k},L_{m})$. Then the coefficient
$l_{k,m}=lk(L_{k},L_{m})$. Then the coefficient ![]() $a_{p-1}$ of the Conway polynomial in degree
$a_{p-1}$ of the Conway polynomial in degree ![]() $p-1$ is
$p-1$ is
In this formula, the sum ranges over spanning trees ![]() $T$ of the complete graph
$T$ of the complete graph ![]() $G$ on the vertex set
$G$ on the vertex set ![]() $\{1,\ldots ,p\}$, and
$\{1,\ldots ,p\}$, and ![]() $(k,m)$ denotes the edge in
$(k,m)$ denotes the edge in ![]() $G$ connecting the
$G$ connecting the ![]() $k$-th and
$k$-th and ![]() $m$-th vertex.
$m$-th vertex.
Proof of Theorem 1.1.
The ‘only if’ part in Theorem 1.1 immediately follows from Theorem 2.1. We start now the proof of the ‘if’ part, which will extend over several sections until the end of the paper.
In order to exhibit braids ![]() $b_{m}$ in Figure 3 as nonconjugate, we follow the approach in [Reference Shinjo19], and evaluate the second coefficient of
$b_{m}$ in Figure 3 as nonconjugate, we follow the approach in [Reference Shinjo19], and evaluate the second coefficient of ![]() $\unicode[STIX]{x1D6FB}$ on the axis-addition link of
$\unicode[STIX]{x1D6FB}$ on the axis-addition link of ![]() $b$. We show that an exchange move alters this coefficient except in a situation described in the following proposition.
$b$. We show that an exchange move alters this coefficient except in a situation described in the following proposition.
Proposition 2.3. Let ![]() $n\geqslant 4$, and
$n\geqslant 4$, and ![]() $K$ be a knot represented as the closure of an
$K$ be a knot represented as the closure of an ![]() $n$-braid
$n$-braid ![]() $b$ admitting an exchange move as in Figure 3. Write the braid permutation
$b$ admitting an exchange move as in Figure 3. Write the braid permutation ![]() $\unicode[STIX]{x1D70B}(b)=(x_{1},x_{2},\ldots ,x_{n})$, where we fix the cyclic ambiguity of
$\unicode[STIX]{x1D70B}(b)=(x_{1},x_{2},\ldots ,x_{n})$, where we fix the cyclic ambiguity of ![]() $x_{i}$ by letting the cycle end on
$x_{i}$ by letting the cycle end on ![]() $x_{n}=n$. Then, unless
$x_{n}=n$. Then, unless ![]() $n=2n^{\prime }+1$ (for
$n=2n^{\prime }+1$ (for ![]() $n^{\prime }\in \mathbb{N}$) and
$n^{\prime }\in \mathbb{N}$) and ![]() $x_{n^{\prime }+1}=1$, all links
$x_{n^{\prime }+1}=1$, all links ![]() $L_{b_{m}}$, for
$L_{b_{m}}$, for ![]() $b_{m}$ as in Figure 3, are distinguished by
$b_{m}$ as in Figure 3, are distinguished by ![]() $a_{3}$.
$a_{3}$.
In the next section, we will be concerned with proving this proposition. The remaining, and more complicated, cases will be settled in Section 4 by looking at the axis-addition link ![]() $L_{b^{2}}$ of the square of
$L_{b^{2}}$ of the square of ![]() $b$.
$b$.
3 Proof of Proposition 2.3
First, we give a lemma needed later. A delta move is a local move defined in [Reference Murakami and Nakanishi15], and this move is equivalent to the move in Figure 5. We consider the delta move on the left-hand side in Figure 6, where the dotted arcs show how the strands connect.

Figure 5. A delta move.
In a way similar to the proof of Lemma 2.2 in [Reference Shinjo19], we can prove the following lemma using Theorem 2.2. (We remind that the linking number and ![]() $i$-th coefficient of the Conway polynomial are written as
$i$-th coefficient of the Conway polynomial are written as ![]() $lk(\cdot ,\cdot )$ and
$lk(\cdot ,\cdot )$ and ![]() $a_{i}(\cdot )$, respectively.)
$a_{i}(\cdot )$, respectively.)
Lemma 3.1. Let ![]() $L$,
$L$, ![]() $L^{\prime }$ and
$L^{\prime }$ and ![]() $l=k_{1}\cup k_{2}\cup k_{3}$ be oriented links related by the local moves as in Figure 6. Then
$l=k_{1}\cup k_{2}\cup k_{3}$ be oriented links related by the local moves as in Figure 6. Then ![]() $a_{3}(L)-a_{3}(L^{\prime })=lk(k_{2},k_{3})-lk(k_{3},k_{1})$.
$a_{3}(L)-a_{3}(L^{\prime })=lk(k_{2},k_{3})-lk(k_{3},k_{1})$.

Figure 6. Three links related by local moves.
Now we are ready to start the proof of the first partial case of Theorem 1.1.
Proof of Proposition 2.3.
We set ![]() $b_{0}=b$. From a braid
$b_{0}=b$. From a braid ![]() $b$, we construct an infinite sequence of braids
$b$, we construct an infinite sequence of braids ![]() $\{b_{m},m\in \mathbb{Z}\}$ as in Figure 3, where
$\{b_{m},m\in \mathbb{Z}\}$ as in Figure 3, where ![]() $m$ and
$m$ and ![]() $-m$ represent
$-m$ represent ![]() $m$ and
$m$ and ![]() $-m$ full twists, respectively. The closures of
$-m$ full twists, respectively. The closures of ![]() $b_{m}$ and
$b_{m}$ and ![]() $b_{m-1}$ (
$b_{m-1}$ (![]() $m\in \mathbb{N}$) are related by ambient isotopy as in Figure 7, where
$m\in \mathbb{N}$) are related by ambient isotopy as in Figure 7, where ![]() $A$ denotes the braid axis. This means that all braids in the sequence close to
$A$ denotes the braid axis. This means that all braids in the sequence close to ![]() $K$.
$K$.

Figure 7. Braids with the same closure.
Since a full twist of ![]() $n$ strings can be deformed as in Figure 8 up to ambient isotopy, the axis-addition link
$n$ strings can be deformed as in Figure 8 up to ambient isotopy, the axis-addition link ![]() $L_{b_{m}}$ of
$L_{b_{m}}$ of ![]() $b_{m}$, which is the leftmost diagram in Figure 9, can be deformed into the rightmost link in the figure, still denoted by
$b_{m}$, which is the leftmost diagram in Figure 9, can be deformed into the rightmost link in the figure, still denoted by ![]() $L_{b_{m}}$. Here
$L_{b_{m}}$. Here ![]() $k$ is the component corresponding to the braid axis and the boxes
$k$ is the component corresponding to the braid axis and the boxes ![]() $m$ and
$m$ and ![]() $-m$ represent
$-m$ represent ![]() $m$-full twists and
$m$-full twists and ![]() $-m$-full twists, respectively.
$-m$-full twists, respectively.

Figure 8. A full twist of ![]() $n$-strings.
$n$-strings.

Figure 9. Deforming ![]() $L_{b_{m}}$ by ambient isotopy (‘a.i.’).
$L_{b_{m}}$ by ambient isotopy (‘a.i.’).
Then there are sequences of links ![]() $L_{b_{m}}=L^{0},L^{1},L^{2},\ldots ,L^{n-1}=L_{b_{m-1}}$ and
$L_{b_{m}}=L^{0},L^{1},L^{2},\ldots ,L^{n-1}=L_{b_{m-1}}$ and ![]() $l^{0},l^{1},l^{2},\ldots ,l^{n-1}$ such that
$l^{0},l^{1},l^{2},\ldots ,l^{n-1}$ such that ![]() $L^{i+1}$ resp.
$L^{i+1}$ resp. ![]() $l^{i}$ are obtained from
$l^{i}$ are obtained from ![]() $L^{i}$ by the delta move
$L^{i}$ by the delta move ![]() $\unicode[STIX]{x1D6E5}_{i}$ resp. the move
$\unicode[STIX]{x1D6E5}_{i}$ resp. the move ![]() $\ast _{i}$, both illustrated in Figures 10 (
$\ast _{i}$, both illustrated in Figures 10 (![]() $i=0$) and 11 (
$i=0$) and 11 (![]() $i=1,\ldots ,n-2$). In particular, there are
$i=1,\ldots ,n-2$). In particular, there are ![]() $n-1$ delta moves transforming
$n-1$ delta moves transforming ![]() $L_{b_{m}}$ into
$L_{b_{m}}$ into ![]() $L_{b_{m-1}}$: the first is chosen to undo a full twist in the box of
$L_{b_{m-1}}$: the first is chosen to undo a full twist in the box of ![]() $m$ on the right diagram of Figure 9, and the other
$m$ on the right diagram of Figure 9, and the other ![]() $n-2$ undo one full winding of the band below that box.
$n-2$ undo one full winding of the band below that box.
By Lemma 3.1, the change in ![]() $a_{3}$ resulting from
$a_{3}$ resulting from ![]() $\unicode[STIX]{x1D6E5}_{0}$ can be obtained as follows:
$\unicode[STIX]{x1D6E5}_{0}$ can be obtained as follows:
where ![]() $l^{0}=l_{1}^{0}\cup l_{2}^{0}\cup l_{3}^{0}$ is the
$l^{0}=l_{1}^{0}\cup l_{2}^{0}\cup l_{3}^{0}$ is the ![]() $3$-component link illustrated in Figure 10.
$3$-component link illustrated in Figure 10.

Figure 10. The moves ![]() $\unicode[STIX]{x1D6E5}_{0}$ and
$\unicode[STIX]{x1D6E5}_{0}$ and ![]() $\ast _{0}$.
$\ast _{0}$.

Figure 11. The local moves on ![]() $L^{i}$.
$L^{i}$.
Next we consider the change in ![]() $a_{3}$ resulting from
$a_{3}$ resulting from ![]() $\unicode[STIX]{x1D6E5}_{i}$ illustrated in the Figure 11 (
$\unicode[STIX]{x1D6E5}_{i}$ illustrated in the Figure 11 (![]() $i=1,2,\ldots ,n-2$). Let
$i=1,2,\ldots ,n-2$). Let ![]() $S_{L^{i}}$ (resp.
$S_{L^{i}}$ (resp. ![]() $S_{l^{i}}$) be a part of
$S_{l^{i}}$) be a part of ![]() $L^{i}$ (resp.
$L^{i}$ (resp. ![]() $l^{i}$) as in the left (resp. right) diagram of Figure 12. Namely
$l^{i}$) as in the left (resp. right) diagram of Figure 12. Namely ![]() $S_{L^{i}}$ and
$S_{L^{i}}$ and ![]() $S_{l^{i}}$ are the unions of
$S_{l^{i}}$ are the unions of ![]() $n$ strings and an unknotted component. Some of these
$n$ strings and an unknotted component. Some of these ![]() $(n-1)$ strings of
$(n-1)$ strings of ![]() $S_{l^{i}}$ belong to
$S_{l^{i}}$ belong to ![]() $l_{1}^{i}$ and the other belong to
$l_{1}^{i}$ and the other belong to ![]() $l_{2}^{i}$. The numbers of strings determine
$l_{2}^{i}$. The numbers of strings determine ![]() $lk(l_{1}^{i},l_{3}^{i})$ and
$lk(l_{1}^{i},l_{3}^{i})$ and ![]() $lk(l_{2}^{i},l_{3}^{i})$.
$lk(l_{2}^{i},l_{3}^{i})$.
By considering how ![]() $S_{l^{i}}-l_{3}^{i}$ has its strings connected, permutations of the
$S_{l^{i}}-l_{3}^{i}$ has its strings connected, permutations of the ![]() $n$ down going strings can be assigned to
$n$ down going strings can be assigned to ![]() $S_{L^{i}}$ and
$S_{L^{i}}$ and ![]() $S_{l^{i}}$, similarly to a braid permutation. We call these the permutations of
$S_{l^{i}}$, similarly to a braid permutation. We call these the permutations of ![]() $S_{L^{i}}$ and
$S_{L^{i}}$ and ![]() $S_{l^{i}}$. Note that the permutation assigned to
$S_{l^{i}}$. Note that the permutation assigned to ![]() $S_{L^{i}}$ is the same as the braid permutation
$S_{L^{i}}$ is the same as the braid permutation ![]() $\unicode[STIX]{x1D70B}(b)$ of
$\unicode[STIX]{x1D70B}(b)$ of ![]() $b$. Since
$b$. Since ![]() $l^{i}-l_{3}^{i}$ is a
$l^{i}-l_{3}^{i}$ is a ![]() $2$ component link, the permutation of
$2$ component link, the permutation of ![]() $S_{l^{i}}$ consists of
$S_{l^{i}}$ consists of ![]() $2$ cycles. To determine the length of these cycles, we observe that the move
$2$ cycles. To determine the length of these cycles, we observe that the move ![]() $\ast _{i}$ corresponds to taking the product of a transposition
$\ast _{i}$ corresponds to taking the product of a transposition ![]() $(n-i,n)$ with the permutation of
$(n-i,n)$ with the permutation of ![]() $S_{L^{i}}$.
$S_{L^{i}}$.

Figure 12.
Take ![]() $j=j(i)$ so that
$j=j(i)$ so that ![]() $n-i=x_{j}$. Then
$n-i=x_{j}$. Then
The cyclic permutations ![]() $(x_{1},x_{2},\ldots ,x_{j-1},n)$ and
$(x_{1},x_{2},\ldots ,x_{j-1},n)$ and ![]() $(x_{j},\ldots ,x_{n-2},x_{n-1})$ correspond to
$(x_{j},\ldots ,x_{n-2},x_{n-1})$ correspond to ![]() $l_{1}^{i}$ and
$l_{1}^{i}$ and ![]() $l_{2}^{i}$, respectively. Remark that the string of
$l_{2}^{i}$, respectively. Remark that the string of ![]() $S_{l^{i}}$ with lower end point
$S_{l^{i}}$ with lower end point ![]() $n$ belongs to
$n$ belongs to ![]() $l_{1}^{i}$, and it does not contribute now to
$l_{1}^{i}$, and it does not contribute now to ![]() $lk(l_{1}^{i},l_{3}^{i})$. By Lemma 3.1,
$lk(l_{1}^{i},l_{3}^{i})$. By Lemma 3.1,
Suppose that ![]() $x_{l}=1$. Then
$x_{l}=1$. Then
 $$\begin{eqnarray}\displaystyle a_{3}(L_{b_{m+1}})-a_{3}(L_{b_{m}}) & = & \displaystyle \{\text{the change in}~a_{3}~\text{resulting from}~\unicode[STIX]{x1D6E5}_{0}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{n-2}\{\text{the change in}~a_{3}~\text{resulting from}~\unicode[STIX]{x1D6E5}_{i}\}\nonumber\\ \displaystyle & = & \displaystyle (n-1)+\mathop{\sum }_{j=1}^{n-1}(2j-n-1)-(2l-n-1)\nonumber\\ \displaystyle & = & \displaystyle -2l+n+1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{3}(L_{b_{m+1}})-a_{3}(L_{b_{m}}) & = & \displaystyle \{\text{the change in}~a_{3}~\text{resulting from}~\unicode[STIX]{x1D6E5}_{0}\}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{n-2}\{\text{the change in}~a_{3}~\text{resulting from}~\unicode[STIX]{x1D6E5}_{i}\}\nonumber\\ \displaystyle & = & \displaystyle (n-1)+\mathop{\sum }_{j=1}^{n-1}(2j-n-1)-(2l-n-1)\nonumber\\ \displaystyle & = & \displaystyle -2l+n+1.\nonumber\end{eqnarray}$$ The difference ![]() $-2l+n+1$ is a constant which does not depend on
$-2l+n+1$ is a constant which does not depend on ![]() $m$. If it is nonzero, the sequence
$m$. If it is nonzero, the sequence ![]() $\{a_{3}(L_{b_{p}}),p\in \mathbb{N}\}$ forms an arithmetic progression with nonzero common difference. When
$\{a_{3}(L_{b_{p}}),p\in \mathbb{N}\}$ forms an arithmetic progression with nonzero common difference. When ![]() $n$ is even,
$n$ is even, ![]() $-2l+n+1$ is odd. This means that
$-2l+n+1$ is odd. This means that ![]() $-2l+n+1\neq 0$. When
$-2l+n+1\neq 0$. When ![]() $n$ is odd, namely
$n$ is odd, namely ![]() $n=2n^{\prime }+1$ for some
$n=2n^{\prime }+1$ for some ![]() $n^{\prime }\in \mathbb{N}$, then
$n^{\prime }\in \mathbb{N}$, then ![]() $-2l+n+1=2(n^{\prime }-l+1)$. Unless
$-2l+n+1=2(n^{\prime }-l+1)$. Unless ![]() $l=n^{\prime }+1$, we have
$l=n^{\prime }+1$, we have ![]() $-2l+n+1\neq 0$. The equation
$-2l+n+1\neq 0$. The equation ![]() $l=n^{\prime }+1$ means that
$l=n^{\prime }+1$ means that ![]() $x_{n^{\prime }+1}=1$. Therefore
$x_{n^{\prime }+1}=1$. Therefore ![]() $a_{3}(L_{b_{m+1}})-a_{3}(L_{b_{m}})$ is nonzero and independent of
$a_{3}(L_{b_{m+1}})-a_{3}(L_{b_{m}})$ is nonzero and independent of ![]() $m$, unless
$m$, unless ![]() $n=2n^{\prime }+1(n^{\prime }\in \mathbb{N})$ and
$n=2n^{\prime }+1(n^{\prime }\in \mathbb{N})$ and ![]() $x_{n^{\prime }+1}=1$. This completes the proof of Proposition 2.3.◻
$x_{n^{\prime }+1}=1$. This completes the proof of Proposition 2.3.◻
4 Remaining knot cases
From now on we assume that ![]() $n=2n^{\prime }+1$ and
$n=2n^{\prime }+1$ and ![]() $\unicode[STIX]{x1D70B}(b)=(x_{1},x_{2},\ldots ,x_{n-1},n)$ with
$\unicode[STIX]{x1D70B}(b)=(x_{1},x_{2},\ldots ,x_{n-1},n)$ with ![]() $x_{n^{\prime }+1}=1$. To prove that
$x_{n^{\prime }+1}=1$. To prove that ![]() $b_{m}$ are nonconjugate, we look at
$b_{m}$ are nonconjugate, we look at ![]() $b_{m}^{2}$: if two braids are conjugate, so are their squares. Note that, when
$b_{m}^{2}$: if two braids are conjugate, so are their squares. Note that, when ![]() $n$ is odd and
$n$ is odd and ![]() $\unicode[STIX]{x1D70B}(b)$ is a cycle, so is
$\unicode[STIX]{x1D70B}(b)$ is a cycle, so is ![]() $\unicode[STIX]{x1D70B}(b^{2})$. Thus
$\unicode[STIX]{x1D70B}(b^{2})$. Thus ![]() $L_{b_{m}^{2}}$ are again 2-component links. We show the following:
$L_{b_{m}^{2}}$ are again 2-component links. We show the following:
Proposition 4.1. Let ![]() $b$ be an
$b$ be an ![]() $n$-braid admitting an exchange move. If
$n$-braid admitting an exchange move. If ![]() $n=2n^{\prime }+1>3$ odd and
$n=2n^{\prime }+1>3$ odd and ![]() $\unicode[STIX]{x1D70B}(b)=(x_{1},x_{2},\ldots ,x_{n-1},n)$ with
$\unicode[STIX]{x1D70B}(b)=(x_{1},x_{2},\ldots ,x_{n-1},n)$ with ![]() $x_{n^{\prime }+1}=1$, then
$x_{n^{\prime }+1}=1$, then ![]() $a_{3}(L_{b_{m}^{2}})$ is a quadratic polynomial in
$a_{3}(L_{b_{m}^{2}})$ is a quadratic polynomial in ![]() $m$ with nonzero quadratic term.
$m$ with nonzero quadratic term.
In particular, there are at most two ![]() $L_{b_{m}^{2}}$ whose
$L_{b_{m}^{2}}$ whose ![]() $a_{3}$ is equal to some fixed value, and so at most two of
$a_{3}$ is equal to some fixed value, and so at most two of ![]() $b_{m}$ are conjugate. Thus with Proposition 4.1, the proof of Theorem 1.1 will be complete.
$b_{m}$ are conjugate. Thus with Proposition 4.1, the proof of Theorem 1.1 will be complete.
Proof of Proposition 4.1.
Let us first simplify the form of ![]() $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and ![]() $\unicode[STIX]{x1D6FD}$ in Figure 2.
$\unicode[STIX]{x1D6FD}$ in Figure 2.
First, every permutation of ![]() $2,\ldots ,n-1$ applied on either side of
$2,\ldots ,n-1$ applied on either side of ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FC})$ can be realized by a braid which can be moved into
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FC})$ can be realized by a braid which can be moved into ![]() $\unicode[STIX]{x1D6FD}$. Thus we can achieve that
$\unicode[STIX]{x1D6FD}$. Thus we can achieve that ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FC})=(1,2)$. So
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FC})=(1,2)$. So
for some pure braid ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ on strands
$\unicode[STIX]{x1D6FC}^{\prime }$ on strands ![]() $1,\ldots ,n-1$.
$1,\ldots ,n-1$.
Then ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})=(x_{1}^{\prime },x_{2}^{\prime },\ldots ,x_{n-2}^{\prime },n)$ is a cycle with
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})=(x_{1}^{\prime },x_{2}^{\prime },\ldots ,x_{n-2}^{\prime },n)$ is a cycle with ![]() $x_{n^{\prime }}^{\prime }=2$ and
$x_{n^{\prime }}^{\prime }=2$ and ![]() $n>x_{j}^{\prime }>2$ otherwise. Now, any such permutation of these
$n>x_{j}^{\prime }>2$ otherwise. Now, any such permutation of these ![]() $x_{j}^{\prime }\neq 2,n$ can be realized by conjugating
$x_{j}^{\prime }\neq 2,n$ can be realized by conjugating ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})$ with a permutation of
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})$ with a permutation of ![]() $3,\ldots ,n-1$. Thus similarly
$3,\ldots ,n-1$. Thus similarly ![]() $\unicode[STIX]{x1D6FD}$ can be conjugated by a braid on strands
$\unicode[STIX]{x1D6FD}$ can be conjugated by a braid on strands ![]() $3,\ldots ,n-1$ (and leaving the other three strands separate).
$3,\ldots ,n-1$ (and leaving the other three strands separate).
Since we achieved that ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FC})$ fixes all of
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FC})$ fixes all of ![]() $3,\ldots ,n-1$, the permutation of
$3,\ldots ,n-1$, the permutation of ![]() $x_{j}^{\prime }\neq 2,n$ in
$x_{j}^{\prime }\neq 2,n$ in ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})$ can be achieved by a conjugation of
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})$ can be achieved by a conjugation of ![]() $b=\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D6FD}$, at the cost of multiplying
$b=\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D6FD}$, at the cost of multiplying ![]() $\unicode[STIX]{x1D6FC}$ by some pure braid on strands
$\unicode[STIX]{x1D6FC}$ by some pure braid on strands ![]() $1,\ldots ,n-1$, which we can absorb into
$1,\ldots ,n-1$, which we can absorb into ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ of (6). Note that in this argument, we make use of the following property: a conjugation by a braid on strands
$\unicode[STIX]{x1D6FC}^{\prime }$ of (6). Note that in this argument, we make use of the following property: a conjugation by a braid on strands ![]() $3,\ldots ,n-1$ commutes with a full twist on strands
$3,\ldots ,n-1$ commutes with a full twist on strands ![]() $2,\ldots ,n-1$, and hence also with the exchange move. Thus if we obtain infinitely many nonconjugate braids by iterated exchange move on the so rearranged braid
$2,\ldots ,n-1$, and hence also with the exchange move. Thus if we obtain infinitely many nonconjugate braids by iterated exchange move on the so rearranged braid ![]() $b$, we obtain these also from the initial braid
$b$, we obtain these also from the initial braid ![]() $b$.
$b$.
This means that we can assume that we can write
for some pure braid ![]() $\unicode[STIX]{x1D6FD}^{\prime }$ on strands
$\unicode[STIX]{x1D6FD}^{\prime }$ on strands ![]() $2,\ldots ,n$, as long as
$2,\ldots ,n$, as long as ![]() $\unicode[STIX]{x1D6FD}_{0}$ is a braid on strands
$\unicode[STIX]{x1D6FD}_{0}$ is a braid on strands ![]() $2,\ldots ,n$ with
$2,\ldots ,n$ with ![]() $\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})$ being a cycle with
$\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D6FD})$ being a cycle with ![]() $x_{n^{\prime }}^{\prime }=2$ when
$x_{n^{\prime }}^{\prime }=2$ when ![]() $x_{n-1}^{\prime }=n$. In the following we choose and fix
$x_{n-1}^{\prime }=n$. In the following we choose and fix
Lemma 4.2. We have ![]() $a_{3}(L_{b_{m}^{2}})-a_{3}(L_{b^{2}})=Am^{2}+Bm+C$ for some (rational) numbers
$a_{3}(L_{b_{m}^{2}})-a_{3}(L_{b^{2}})=Am^{2}+Bm+C$ for some (rational) numbers ![]() $A,B,C$ (depending, a priori, on
$A,B,C$ (depending, a priori, on ![]() $n$ and
$n$ and ![]() $b$). Moreover,
$b$). Moreover, ![]() $A$ does not depend on the braids
$A$ does not depend on the braids ![]() $\unicode[STIX]{x1D6FC}^{\prime }$,
$\unicode[STIX]{x1D6FC}^{\prime }$, ![]() $\unicode[STIX]{x1D6FD}^{\prime }$ in the presentation
$\unicode[STIX]{x1D6FD}^{\prime }$ in the presentation
Proof. The axis link of ![]() $L_{b_{m}^{2}}$ can be built and simplified similarly to Figure 9. The procedure is shown in Figure 13. In this case we involve the up going strand also on the left of
$L_{b_{m}^{2}}$ can be built and simplified similarly to Figure 9. The procedure is shown in Figure 13. In this case we involve the up going strand also on the left of ![]() $b$. Now we can cancel the full twists on
$b$. Now we can cancel the full twists on ![]() $n-2$ strands in
$n-2$ strands in ![]() $b_{m}^{2}$ by creating pairs of bands that circle, in the opposite way, around the middle
$b_{m}^{2}$ by creating pairs of bands that circle, in the opposite way, around the middle ![]() $n-2$ strands. See Figure 14. It shows the case
$n-2$ strands. See Figure 14. It shows the case ![]() $n=7$ and
$n=7$ and ![]() $m=1$. (One of the pairs of circling bands, the one at the bottom, untangles, so we have 3 such pairs.) We indicate the braids
$m=1$. (One of the pairs of circling bands, the one at the bottom, untangles, so we have 3 such pairs.) We indicate the braids ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ and
$\unicode[STIX]{x1D6FC}^{\prime }$ and ![]() $\unicode[STIX]{x1D6FD}^{\prime }$ just by a dashed line, showing where they have to be inserted.
$\unicode[STIX]{x1D6FD}^{\prime }$ just by a dashed line, showing where they have to be inserted.

Figure 13. Building ![]() $L_{b_{m}^{2}}$. The move from the first to the second diagram consists in inserting two groups of
$L_{b_{m}^{2}}$. The move from the first to the second diagram consists in inserting two groups of ![]() $m$ full twists and two groups of
$m$ full twists and two groups of ![]() $-m$ full twists on all
$-m$ full twists on all ![]() $n+2$ strands, and then grouping out the subtwists on the central
$n+2$ strands, and then grouping out the subtwists on the central ![]() $n-2$ strands into a part denoted by a box.
$n-2$ strands into a part denoted by a box.

Figure 14. ![]() $L_{b_{m}^{2}}$ (for
$L_{b_{m}^{2}}$ (for ![]() $m=1$).
$m=1$).

Figure 15. Simplifying ![]() $L_{b_{m}^{2}}$ (for
$L_{b_{m}^{2}}$ (for ![]() $m=1$).
$m=1$).
Now the bands ![]() $\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D6FF}$ and ![]() $\unicode[STIX]{x1D701}$ cancel, and
$\unicode[STIX]{x1D701}$ cancel, and ![]() $\unicode[STIX]{x1D702}$ trivializes. Then,
$\unicode[STIX]{x1D702}$ trivializes. Then, ![]() $\unicode[STIX]{x1D703}$ and
$\unicode[STIX]{x1D703}$ and ![]() $\unicode[STIX]{x1D700}$ cancel by a half-turn (and all their internal twists cancel; see Figure 15), but to cancel them further, we need to move the band past
$\unicode[STIX]{x1D700}$ cancel by a half-turn (and all their internal twists cancel; see Figure 15), but to cancel them further, we need to move the band past ![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D701}$ in the encircled region of Figure 16. (For general
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D701}$ in the encircled region of Figure 16. (For general ![]() $m$, the parts
$m$, the parts ![]() $\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D6FF}$ and ![]() $\unicode[STIX]{x1D701}$ will have
$\unicode[STIX]{x1D701}$ will have ![]() $|m|-1$ full turns of the band around the other
$|m|-1$ full turns of the band around the other ![]() $n-2$ strings in the opposite direction.)
$n-2$ strings in the opposite direction.)

Figure 16. Simplified ![]() $L_{b_{m}^{2}}$ (for
$L_{b_{m}^{2}}$ (for ![]() $m=1$).
$m=1$).
Next, ![]() $\unicode[STIX]{x1D6FE}$ can be deleted at the cost of changing
$\unicode[STIX]{x1D6FE}$ can be deleted at the cost of changing ![]() $a_{3}$ by a quantity linear in
$a_{3}$ by a quantity linear in ![]() $m$ (whose linear terms may depend on
$m$ (whose linear terms may depend on ![]() $n$,
$n$, ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ and
$\unicode[STIX]{x1D6FC}^{\prime }$ and ![]() $\unicode[STIX]{x1D6FD}^{\prime }$). This can be seen from Lemma 3.1, in the way we applied it in Section 3. It must be realized that, in spite of the bands
$\unicode[STIX]{x1D6FD}^{\prime }$). This can be seen from Lemma 3.1, in the way we applied it in Section 3. It must be realized that, in spite of the bands ![]() $\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D6FF}$ and ![]() $\unicode[STIX]{x1D701}$ in the lower part of the figure, the linking number of
$\unicode[STIX]{x1D701}$ in the lower part of the figure, the linking number of ![]() $l_{1}^{i}$ and
$l_{1}^{i}$ and ![]() $l_{2}^{i}$ with
$l_{2}^{i}$ with ![]() $l_{3}^{i}$ does not depend on
$l_{3}^{i}$ does not depend on ![]() $m$. Thus the change of
$m$. Thus the change of ![]() $a_{3}$ under undoing one full twist of
$a_{3}$ under undoing one full twist of ![]() $\unicode[STIX]{x1D6FE}$ does not depend on
$\unicode[STIX]{x1D6FE}$ does not depend on ![]() $m$ either.
$m$ either.
This means that, for the purpose of proving Lemma 4.2, we can disregard the band ![]() $\unicode[STIX]{x1D6FE}$, and so we assume that it is trivial. Then we obtain from
$\unicode[STIX]{x1D6FE}$, and so we assume that it is trivial. Then we obtain from ![]() $L_{b_{m}^{2}}$ the links
$L_{b_{m}^{2}}$ the links ![]() $K_{m}$ as shown (for
$K_{m}$ as shown (for ![]() $m=1,2$ and
$m=1,2$ and ![]() $n=7$) in Figure 17.
$n=7$) in Figure 17.

Figure 17. ![]() $K_{m}$.
$K_{m}$.
Using the relation (3), we can write
where ![]() $L_{i}=L_{m,i}$ are 3-component links obtained from
$L_{i}=L_{m,i}$ are 3-component links obtained from ![]() $K_{m+1}$ by changing some and smoothing exactly one of the 4 crossings in the encircled part. (Apply the skein relation to these 4 crossings in any order.)
$K_{m+1}$ by changing some and smoothing exactly one of the 4 crossings in the encircled part. (Apply the skein relation to these 4 crossings in any order.)
Now, it is easy to observe that among the 3 linking numbers between the components of each ![]() $L_{i}$, only one (the one not involving the braid axis) depends, linearly, on
$L_{i}$, only one (the one not involving the braid axis) depends, linearly, on ![]() $m$ (a dependence which holds for either signs of
$m$ (a dependence which holds for either signs of ![]() $m$), and
$m$), and ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ and
$\unicode[STIX]{x1D6FC}^{\prime }$ and ![]() $\unicode[STIX]{x1D6FD}^{\prime }$ affect all 3 linking numbers only by some additive constant.
$\unicode[STIX]{x1D6FD}^{\prime }$ affect all 3 linking numbers only by some additive constant.
It follows then from Theorem 2.2 that ![]() $a_{3}(K_{m+1})-a_{3}(K_{m})$ is a linear expression in
$a_{3}(K_{m+1})-a_{3}(K_{m})$ is a linear expression in ![]() $m$ with a linear term independent on
$m$ with a linear term independent on ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ and
$\unicode[STIX]{x1D6FC}^{\prime }$ and ![]() $\unicode[STIX]{x1D6FD}^{\prime }$. By inductive iteration, we obtain the claim of Lemma 4.2.◻
$\unicode[STIX]{x1D6FD}^{\prime }$. By inductive iteration, we obtain the claim of Lemma 4.2.◻
With Lemma 4.2, for the proof of Proposition 4.1, it is legitimate to assume that ![]() $\unicode[STIX]{x1D6FC}^{\prime }$ and
$\unicode[STIX]{x1D6FC}^{\prime }$ and ![]() $\unicode[STIX]{x1D6FD}^{\prime }$ are trivial, and (7) becomes
$\unicode[STIX]{x1D6FD}^{\prime }$ are trivial, and (7) becomes
It is not difficult to evaluate the quadratic coefficient ![]() $A$ in the lemma for this special case.
$A$ in the lemma for this special case.
Now,
and so it is enough to show that the right-hand side of this equation, call it ![]() $D_{n}$, does not vanish for any odd
$D_{n}$, does not vanish for any odd ![]() $n\geqslant 5$.
$n\geqslant 5$.
Again, one can express ![]() $a_{3}(K_{1})-a_{3}(K_{0})$ and
$a_{3}(K_{1})-a_{3}(K_{0})$ and ![]() $a_{3}(K_{0})-a_{3}(K_{-1})$ using (8). Next, observe that, essentially because the action of
$a_{3}(K_{0})-a_{3}(K_{-1})$ using (8). Next, observe that, essentially because the action of ![]() $\unicode[STIX]{x1D70B}(b^{2})$ on intermediate strands is to shift by
$\unicode[STIX]{x1D70B}(b^{2})$ on intermediate strands is to shift by ![]() $4$ to left or right, the replacement of any odd
$4$ to left or right, the replacement of any odd ![]() $n\geqslant 5$ by
$n\geqslant 5$ by ![]() $n+4k$ alters the component linking numbers of the links
$n+4k$ alters the component linking numbers of the links ![]() $L_{i}$ in (8) by multiples of
$L_{i}$ in (8) by multiples of ![]() $k$. It follows then that
$k$. It follows then that ![]() $D_{n+4k}$ is a certain quadratic expression in
$D_{n+4k}$ is a certain quadratic expression in ![]() $k\geqslant 0$ for
$k\geqslant 0$ for ![]() $n=5$ and
$n=5$ and ![]() $n=7$. To determine these expressions, one can make a direct calculation using (8) and Theorem 2.2. This is, however, somewhat tedious and error-prone. Thus we also used a different method for verification.
$n=7$. To determine these expressions, one can make a direct calculation using (8) and Theorem 2.2. This is, however, somewhat tedious and error-prone. Thus we also used a different method for verification.
We drew, as in Figure 18, the links ![]() $K_{\pm 1}$ and
$K_{\pm 1}$ and ![]() $K_{0}$ for
$K_{0}$ for ![]() $k=0,1,2$ in either case (i.e.,
$k=0,1,2$ in either case (i.e., ![]() $n=5,7,\ldots ,15$), and calculated
$n=5,7,\ldots ,15$), and calculated ![]() $c_{i}=a_{3}(K_{i})$ by computer.
$c_{i}=a_{3}(K_{i})$ by computer.

Figure 18. ![]() $K_{m}$ for
$K_{m}$ for ![]() $|m|\leqslant 1$ and
$|m|\leqslant 1$ and ![]() $n=5,7$.
$n=5,7$.
The most complicated diagrams have 118 crossings, but it took a total of 10.5 seconds to evaluate ![]() $a_{3}$ on all 18 diagrams using the skein polynomial truncation algorithm of [Reference Stoimenow23]. The result is shown below:
$a_{3}$ on all 18 diagrams using the skein polynomial truncation algorithm of [Reference Stoimenow23]. The result is shown below:

From this one determines that
This is never zero for any ![]() $k\geqslant 0$. (It vanishes, however, for
$k\geqslant 0$. (It vanishes, however, for ![]() $k=-1$, which is in nice accordance with the triviality of the cases
$k=-1$, which is in nice accordance with the triviality of the cases ![]() $n=1,3$.) With this the proof of Proposition 4.1 is concluded.
$n=1,3$.) With this the proof of Proposition 4.1 is concluded.
This also completes the proof of Theorem 1.1.◻
5 Table
It is a consequence of Theorem 1.1 that any composite knot ![]() $K$ of braid index
$K$ of braid index ![]() $b(K)\geqslant 4$ has infinitely many nonconjugate minimal braid representatives. (This insight was also obtained in [Reference Stoimenow22].)
$b(K)\geqslant 4$ has infinitely many nonconjugate minimal braid representatives. (This insight was also obtained in [Reference Stoimenow22].)
In the tables of prime knots ![]() $K$ of crossing number
$K$ of crossing number ![]() $c(K)\leqslant 10$ [Reference Rolfsen17, appendix], we found that most knots of
$c(K)\leqslant 10$ [Reference Rolfsen17, appendix], we found that most knots of ![]() $b(K)\geqslant 4$, except 7 knots for
$b(K)\geqslant 4$, except 7 knots for ![]() $c(K)=9$ and 15 knots for
$c(K)=9$ and 15 knots for ![]() $c(K)=10$, have a minimal representative admitting an exchange move. So these knots have infinitely many conjugacy classes of minimal braid representatives.
$c(K)=10$, have a minimal representative admitting an exchange move. So these knots have infinitely many conjugacy classes of minimal braid representatives.
The below list gives 4-braid representatives admitting an exchange move for 95 knots of braid index 4 (up to mirroring) in Rolfsen’s tables. An integer ![]() $i>0$ means
$i>0$ means ![]() $\unicode[STIX]{x1D70E}_{i}$, an
$\unicode[STIX]{x1D70E}_{i}$, an ![]() $i<0$ stands for
$i<0$ stands for ![]() $\unicode[STIX]{x1D70E}_{-i}^{-1}$. Note that an
$\unicode[STIX]{x1D70E}_{-i}^{-1}$. Note that an ![]() $n$-braid word admits an exchange move up to cyclic permutation if and only if it has no (cyclic) subword of the form
$n$-braid word admits an exchange move up to cyclic permutation if and only if it has no (cyclic) subword of the form
We shifted, as in [Reference Burde and Zieschang6], indices down by 1 for ![]() $10_{163},\ldots ,10_{166}$ to discard Perko’s duplication. Thus, for example, the knot written below as
$10_{163},\ldots ,10_{166}$ to discard Perko’s duplication. Thus, for example, the knot written below as ![]() $10_{162}$ is Rolfsen’s
$10_{162}$ is Rolfsen’s ![]() $10_{163}$.
$10_{163}$.
A further mistake in Rolfsen’s tables is that therein ![]() $10_{83}$ and
$10_{83}$ and ![]() $10_{86}$ are swapped: the Conway notation and Alexander polynomial for each one refers to the diagram of the other. The convention taken here is that we interchange Conway notations and Alexander polynomials to fix the mismatch (as in the corrected reprinting of Rolfsen’s book), and not the diagrams (as, e.g., in [Reference Kawauchi12]).
$10_{86}$ are swapped: the Conway notation and Alexander polynomial for each one refers to the diagram of the other. The convention taken here is that we interchange Conway notations and Alexander polynomials to fix the mismatch (as in the corrected reprinting of Rolfsen’s book), and not the diagrams (as, e.g., in [Reference Kawauchi12]).

The 22 knots of braid index 4 for which we could not find a 4-braid admitting an exchange move are:

Among the 5- and 6-braid knots in the table, all have a minimal braid admitting an exchange move. This can be checked from the representatives given in [Reference Stoimenow24]. It is easy to see that the (cyclic) shape (9) (with ![]() $n=5,6$) can be avoided after possibly applying some commutativity relations.
$n=5,6$) can be avoided after possibly applying some commutativity relations.
Acknowledgments
This work was carried out under support by the Brain Korea 21 (BK21) Project of the Ministry of Education & Human Resources Development of the Republic of Korea. The authors are grateful to KAIST, Daejeon, Korea for its hospitality.