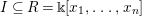1 Introduction
Let
![]() $A$
be a Noetherian local ring that admits a surjection from an
$A$
be a Noetherian local ring that admits a surjection from an
![]() $n$
-dimensional regular local ring
$n$
-dimensional regular local ring
![]() $(R,\mathfrak{m})$
containing its residue field
$(R,\mathfrak{m})$
containing its residue field
![]() $\Bbbk$
, and let
$\Bbbk$
, and let
![]() $I\subseteq R$
be the kernel of the surjection. In [Reference Lyubeznik13], Lyubeznik introduced a new set of invariants
$I\subseteq R$
be the kernel of the surjection. In [Reference Lyubeznik13], Lyubeznik introduced a new set of invariants
![]() $\unicode[STIX]{x1D706}_{p,i}(A)$
as the
$\unicode[STIX]{x1D706}_{p,i}(A)$
as the
![]() $p$
th Bass number of the local cohomology module
$p$
th Bass number of the local cohomology module
![]() $H_{I}^{n-i}(R)$
. That is,
$H_{I}^{n-i}(R)$
. That is,
and they depend only on
![]() $A$
,
$A$
,
![]() $i$
and
$i$
and
![]() $p$
, but not on the choice of
$p$
, but not on the choice of
![]() $R$
or the surjection
$R$
or the surjection
![]() $R\longrightarrow A$
. In the seminal works of Huneke and Sharp [Reference Huneke and Sharp10] and Lyubeznik [Reference Lyubeznik13], it is proven that these Bass numbers are all finite. Denoting
$R\longrightarrow A$
. In the seminal works of Huneke and Sharp [Reference Huneke and Sharp10] and Lyubeznik [Reference Lyubeznik13], it is proven that these Bass numbers are all finite. Denoting
![]() $d=\text{dim }A$
, Lyubeznik numbers satisfy the following propertiesFootnote
1
.
$d=\text{dim }A$
, Lyubeznik numbers satisfy the following propertiesFootnote
1
.
(i)
 $\unicode[STIX]{x1D706}_{p,i}(A)\neq 0$
implies
$\unicode[STIX]{x1D706}_{p,i}(A)\neq 0$
implies
 $0\leqslant p\leqslant i\leqslant d$
.
$0\leqslant p\leqslant i\leqslant d$
.(ii)
 $\unicode[STIX]{x1D706}_{d,d}(A)\neq 0$
.
$\unicode[STIX]{x1D706}_{d,d}(A)\neq 0$
.(iii) Euler characteristic:
 $$\begin{eqnarray}\mathop{\sum }_{0\leqslant p,i\leqslant d}(-1)^{p-i}\unicode[STIX]{x1D706}_{p,i}(A)=1.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{0\leqslant p,i\leqslant d}(-1)^{p-i}\unicode[STIX]{x1D706}_{p,i}(A)=1.\end{eqnarray}$$
Therefore, we can collect them in the so-called Lyubeznik table:
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(A)=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}_{0,0} & \cdots \, & \unicode[STIX]{x1D706}_{0,d}\\ & \ddots & \vdots \\ & & \unicode[STIX]{x1D706}_{d,d}\\ \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(A)=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D706}_{0,0} & \cdots \, & \unicode[STIX]{x1D706}_{0,d}\\ & \ddots & \vdots \\ & & \unicode[STIX]{x1D706}_{d,d}\\ \end{array}\right),\end{eqnarray}$$
and we say that the Lyubeznik table is trivial if
![]() $\unicode[STIX]{x1D706}_{d,d}=1$
and the rest of these invariants vanish.
$\unicode[STIX]{x1D706}_{d,d}=1$
and the rest of these invariants vanish.
Despite their algebraic nature, Lyubeznik numbers also provide some geometrical and topological information, as was already pointed out in [Reference Lyubeznik13]. For instance, in the case of isolated singularities, Lyubeznik numbers can be described in terms of certain singular cohomology groups in characteristic zero (see [Reference García López and Sabbah6]) or étale cohomology groups in positive characteristic (see [Reference Blickle4, Reference Blickle and Bondu5]). The highest Lyubeznik number
![]() $\unicode[STIX]{x1D706}_{d,d}(A)$
can be described using the so-called Hochster and Huneke graph, as has been proved in [Reference Lyubeznik15, Reference Zhang31]. However, very little is known about the possible configurations of Lyubeznik tables except for low-dimension cases [Reference Kawasaki12, Reference Walther24] or the just mentioned case of isolated singularities.
$\unicode[STIX]{x1D706}_{d,d}(A)$
can be described using the so-called Hochster and Huneke graph, as has been proved in [Reference Lyubeznik15, Reference Zhang31]. However, very little is known about the possible configurations of Lyubeznik tables except for low-dimension cases [Reference Kawasaki12, Reference Walther24] or the just mentioned case of isolated singularities.
In Section 2, we give some new constraints to the possible configurations of Lyubeznik tables. Namely, the main result, Theorem 2.1, establishes some consecutiveness of the nonvanishing superdiagonals of the Lyubeznik tables using spectral sequence arguments.
In Section 3, we introduce a new set of invariants associated to the linear strands of a minimal free resolution of a
![]() $\mathbb{Z}$
-graded ideal
$\mathbb{Z}$
-graded ideal
![]() $I\subseteq R=\Bbbk [x_{1},\ldots ,x_{n}]$
. It turns out that these new invariants satisfy some analogous properties to those of Lyubeznik numbers, including the aforementioned consecutiveness property. Moreover, we provide a Thom–Sebastiani type formula for these invariants, which is a refinement of the formula for Betti numbers given by Jacques and Katzman in [Reference Jacques and Katzman11]. This section should be of independent interest, and we hope it can be further developed in future work.
$I\subseteq R=\Bbbk [x_{1},\ldots ,x_{n}]$
. It turns out that these new invariants satisfy some analogous properties to those of Lyubeznik numbers, including the aforementioned consecutiveness property. Moreover, we provide a Thom–Sebastiani type formula for these invariants, which is a refinement of the formula for Betti numbers given by Jacques and Katzman in [Reference Jacques and Katzman11]. This section should be of independent interest, and we hope it can be further developed in future work.
In the rest of the paper, we treat the case where
![]() $I$
is a monomial ideal in a polynomial ring
$I$
is a monomial ideal in a polynomial ring
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
, and
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
, and
![]() $\mathfrak{m}=(x_{1},\ldots ,x_{n})$
is the graded maximal ideal. Bass numbers are invariant with respect to completion, so we consider
$\mathfrak{m}=(x_{1},\ldots ,x_{n})$
is the graded maximal ideal. Bass numbers are invariant with respect to completion, so we consider
![]() $\unicode[STIX]{x1D706}_{p,i}(R/I)=\unicode[STIX]{x1D706}_{p,i}(\widehat{R}/I\widehat{R})$
, where
$\unicode[STIX]{x1D706}_{p,i}(R/I)=\unicode[STIX]{x1D706}_{p,i}(\widehat{R}/I\widehat{R})$
, where
![]() $\widehat{R}=\Bbbk [\![x_{1},\ldots ,x_{n}]\!]$
. In this sense, our study on the Lyubeznik tables of monomial ideals is a (very) special case of that for local rings. However, advanced techniques in combinatorial commutative algebra are very effective in this setting, and we can go much further than the general case, so we hope that monomial ideals are good test cases for the study of Lyubeznik tables.
$\widehat{R}=\Bbbk [\![x_{1},\ldots ,x_{n}]\!]$
. In this sense, our study on the Lyubeznik tables of monomial ideals is a (very) special case of that for local rings. However, advanced techniques in combinatorial commutative algebra are very effective in this setting, and we can go much further than the general case, so we hope that monomial ideals are good test cases for the study of Lyubeznik tables.
Since local cohomology modules satisfy
![]() $H_{I}^{i}(R)\cong H_{\sqrt{I}}^{i}(R)$
, we often assume that a monomial ideal
$H_{I}^{i}(R)\cong H_{\sqrt{I}}^{i}(R)$
, we often assume that a monomial ideal
![]() $I$
is squarefree, that is,
$I$
is squarefree, that is,
![]() $I=\sqrt{I}$
. In this case,
$I=\sqrt{I}$
. In this case,
![]() $I$
coincides with the Stanley–Reisner ideal
$I$
coincides with the Stanley–Reisner ideal
![]() $I_{\unicode[STIX]{x1D6E5}}$
of a simplicial complex
$I_{\unicode[STIX]{x1D6E5}}$
of a simplicial complex
![]() $\unicode[STIX]{x1D6E5}\subseteq 2^{\{1,\ldots ,n\}}$
. More precisely,
$\unicode[STIX]{x1D6E5}\subseteq 2^{\{1,\ldots ,n\}}$
. More precisely,
The Stanley–Reisner ring
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
is one of the most fundamental tools in combinatorial commutative algebra, and it is known that
$R/I_{\unicode[STIX]{x1D6E5}}$
is one of the most fundamental tools in combinatorial commutative algebra, and it is known that
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
reflects topological properties of the geometric realization
$R/I_{\unicode[STIX]{x1D6E5}}$
reflects topological properties of the geometric realization
![]() $|\unicode[STIX]{x1D6E5}|$
of
$|\unicode[STIX]{x1D6E5}|$
of
![]() $\unicode[STIX]{x1D6E5}$
in several ways.
$\unicode[STIX]{x1D6E5}$
in several ways.
In Section 4, we get a deeper insight to the relation, given by the first author and Vahidi in [Reference Àlvarez Montaner and Vahidi1], between Lyubeznik numbers of monomial ideals and the linear strands of their associated Alexander dual ideals. In particular, we give a different approach to the fact proved in [Reference Àlvarez Montaner2] that if
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
is sequentially Cohen–Macaulay, then its Lyubeznik table is trivial. We also provide a Thom–Sebastiani type formula for Lyubeznik numbers.
$R/I_{\unicode[STIX]{x1D6E5}}$
is sequentially Cohen–Macaulay, then its Lyubeznik table is trivial. We also provide a Thom–Sebastiani type formula for Lyubeznik numbers.
One of the main results of this paper is left for Section 5. Namely, Theorem 5.3 states that Lyubeznik numbers of Stanley–Reisner rings are not only algebraic invariants but also topological invariants, meaning that the Lyubeznik numbers of
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
depend on the homeomorphic class of the geometric realization
$R/I_{\unicode[STIX]{x1D6E5}}$
depend on the homeomorphic class of the geometric realization
![]() $|\unicode[STIX]{x1D6E5}|$
of
$|\unicode[STIX]{x1D6E5}|$
of
![]() $\unicode[STIX]{x1D6E5}$
and the characteristic of the base field.
$\unicode[STIX]{x1D6E5}$
and the characteristic of the base field.
The proof of this result is quite technical and is irrelevant to the other parts of the paper, so we decided to put it in the final section. We also remark that this result holds in a wider setting. More precisely, if
![]() $R$
is a normal simplicial semigroup ring that is Gorenstein, and
$R$
is a normal simplicial semigroup ring that is Gorenstein, and
![]() $I$
is a monomial ideal, then the corresponding result holds. We work in this general setting, since the proof is the same as in the polynomial ring case.
$I$
is a monomial ideal, then the corresponding result holds. We work in this general setting, since the proof is the same as in the polynomial ring case.
2 Consecutiveness of nontrivial superdiagonals of the Lyubeznik table
It seems to be a very difficult task to give a full description of the possible configurations of Lyubeznik tables of any local ring, and only a few results can be found in the literature. The aim of this section is to give some constraints to the possible configurations of Lyubeznik tables, aside from the Euler characteristic formula.
Let
![]() $(R,\mathfrak{m})$
be a regular local ring of dimension
$(R,\mathfrak{m})$
be a regular local ring of dimension
![]() $n$
containing its residue field
$n$
containing its residue field
![]() $\Bbbk$
, and let
$\Bbbk$
, and let
![]() $I\subseteq R$
be any ideal with
$I\subseteq R$
be any ideal with
![]() $\dim R/I=d$
. For each
$\dim R/I=d$
. For each
![]() $j\in \mathbb{N}$
with
$j\in \mathbb{N}$
with
![]() $0\leqslant j\leqslant d$
, set
$0\leqslant j\leqslant d$
, set
For example,
![]() $\unicode[STIX]{x1D70C}_{0}(R/I)$
(resp.
$\unicode[STIX]{x1D70C}_{0}(R/I)$
(resp.
![]() $\unicode[STIX]{x1D70C}_{1}(R/I)$
) is the sum of the entries in the diagonal (resp. superdiagonal) of the Lyubeznik table
$\unicode[STIX]{x1D70C}_{1}(R/I)$
) is the sum of the entries in the diagonal (resp. superdiagonal) of the Lyubeznik table
![]() $\unicode[STIX]{x1D6EC}(R/I)$
. Clearly,
$\unicode[STIX]{x1D6EC}(R/I)$
. Clearly,
![]() $\sum _{j\in \mathbb{N}}(-1)^{j}\unicode[STIX]{x1D70C}_{j}(R/I)=1$
. We say that
$\sum _{j\in \mathbb{N}}(-1)^{j}\unicode[STIX]{x1D70C}_{j}(R/I)=1$
. We say that
![]() $\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial if
$\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial if
Clearly,
![]() $\unicode[STIX]{x1D6EC}(R/I)$
is nontrivial if and only if
$\unicode[STIX]{x1D6EC}(R/I)$
is nontrivial if and only if
![]() $\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial for some
$\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial for some
![]() $j$
.
$j$
.
It is easy to see that
![]() $\unicode[STIX]{x1D706}_{0,d}(R/I)=0$
if
$\unicode[STIX]{x1D706}_{0,d}(R/I)=0$
if
![]() $d\geqslant 1$
and
$d\geqslant 1$
and
![]() $\unicode[STIX]{x1D706}_{0,d}(R/I)=1$
if
$\unicode[STIX]{x1D706}_{0,d}(R/I)=1$
if
![]() $d=0$
. That is,
$d=0$
. That is,
![]() $\unicode[STIX]{x1D70C}_{d}(R/I)$
is always trivial.
$\unicode[STIX]{x1D70C}_{d}(R/I)$
is always trivial.
A key fact that we use in this section is that local cohomology modules have a natural structure over the ring of
![]() $k$
-linear differential operators
$k$
-linear differential operators
![]() $D_{R|k}$
(see [Reference Lyubeznik13, Reference Lyubeznik14]). In fact, they are
$D_{R|k}$
(see [Reference Lyubeznik13, Reference Lyubeznik14]). In fact, they are
![]() $D_{R|k}$
-modules of finite length (see [Reference Björk3, Theorem 2.7.13] and [Reference Lyubeznik13, Example 2.2] for the case of characteristic zero and [Reference Lyubeznik14, Theorem 5.7] in positive characteristic). In particular, Lyubeznik numbers are nothing but the length as a
$D_{R|k}$
-modules of finite length (see [Reference Björk3, Theorem 2.7.13] and [Reference Lyubeznik13, Example 2.2] for the case of characteristic zero and [Reference Lyubeznik14, Theorem 5.7] in positive characteristic). In particular, Lyubeznik numbers are nothing but the length as a
![]() $D_{R|k}$
-module of the local cohomology modules
$D_{R|k}$
-module of the local cohomology modules
![]() $H_{\mathfrak{m}}^{p}(H_{I}^{n-i}(R))$
. That is,
$H_{\mathfrak{m}}^{p}(H_{I}^{n-i}(R))$
. That is,
The
![]() $D_{R|k}$
-module length, which will be denoted simply as
$D_{R|k}$
-module length, which will be denoted simply as
![]() $e(-)$
, is an additive function. That is, given a short exact sequence of holonomic
$e(-)$
, is an additive function. That is, given a short exact sequence of holonomic
![]() $D_{R|k}$
-modules
$D_{R|k}$
-modules
![]() $0\longrightarrow M_{1}\longrightarrow M_{2}\longrightarrow M_{3}\longrightarrow 0$
, we have
$0\longrightarrow M_{1}\longrightarrow M_{2}\longrightarrow M_{3}\longrightarrow 0$
, we have
The main result of this section is the following.
Theorem 2.1. Let
![]() $(R,\mathfrak{m})$
be a regular local ring of dimension
$(R,\mathfrak{m})$
be a regular local ring of dimension
![]() $n$
containing its residue field
$n$
containing its residue field
![]() $\Bbbk$
, and let
$\Bbbk$
, and let
![]() $I\subseteq R$
be any ideal with
$I\subseteq R$
be any ideal with
![]() $\dim R/I=d$
. Then, we have the following.
$\dim R/I=d$
. Then, we have the following.
∙ If
 $\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial for some
$\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial for some
 $j$
with
$j$
with
 $0<j<d$
, then either
$0<j<d$
, then either
 $\unicode[STIX]{x1D70C}_{j-1}(R/I)$
or
$\unicode[STIX]{x1D70C}_{j-1}(R/I)$
or
 $\unicode[STIX]{x1D70C}_{j+1}(R/I)$
is nontrivial.
$\unicode[STIX]{x1D70C}_{j+1}(R/I)$
is nontrivial.∙ If
 $\unicode[STIX]{x1D70C}_{0}(R/I)$
is nontrivial, then so is
$\unicode[STIX]{x1D70C}_{0}(R/I)$
is nontrivial, then so is
 $\unicode[STIX]{x1D70C}_{1}(R/I)$
.
$\unicode[STIX]{x1D70C}_{1}(R/I)$
.
Proof. Consider Grothendieck’s spectral sequence
This is a spectral sequence of
![]() $D_{R|k}$
-modules where
$D_{R|k}$
-modules where
![]() $\unicode[STIX]{x1D706}_{p,i}(R/I)=e(E_{2}^{p,n-i})$
. Notice also that the local cohomology modules
$\unicode[STIX]{x1D706}_{p,i}(R/I)=e(E_{2}^{p,n-i})$
. Notice also that the local cohomology modules
![]() $H_{\mathfrak{m}}^{r}(R)$
vanish for all
$H_{\mathfrak{m}}^{r}(R)$
vanish for all
![]() $r\neq n$
, and in this case
$r\neq n$
, and in this case
![]() $e(H_{\mathfrak{m}}^{n}(R))=1$
.
$e(H_{\mathfrak{m}}^{n}(R))=1$
.
We prove the assertion by contradiction. Therefore, assume that
![]() $\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial for some
$\unicode[STIX]{x1D70C}_{j}(R/I)$
is nontrivial for some
![]() $0<j<d$
, but both
$0<j<d$
, but both
![]() $\unicode[STIX]{x1D70C}_{j-1}(R/I)$
and
$\unicode[STIX]{x1D70C}_{j-1}(R/I)$
and
![]() $\unicode[STIX]{x1D70C}_{j+1}(R/I)$
are trivial. (The case
$\unicode[STIX]{x1D70C}_{j+1}(R/I)$
are trivial. (The case
![]() $j=0$
can be proved by a similar argument.) We have some
$j=0$
can be proved by a similar argument.) We have some
![]() $p,i$
with
$p,i$
with
![]() $i=p+j$
such that
$i=p+j$
such that
![]() $\unicode[STIX]{x1D706}_{p,i}(R/I)\neq 0$
(equivalently,
$\unicode[STIX]{x1D706}_{p,i}(R/I)\neq 0$
(equivalently,
![]() $E_{2}^{p,n-i}\neq 0$
). Consider the maps on
$E_{2}^{p,n-i}\neq 0$
). Consider the maps on
![]() $E_{2}$
-terms
$E_{2}$
-terms
We show that
![]() $d_{2}=d_{2}^{\prime }=0$
.
$d_{2}=d_{2}^{\prime }=0$
.
Consider first the case
![]() $j>1$
. We have
$j>1$
. We have
![]() $E_{2}^{p-2,n-i+1}=E_{2}^{p+2,n-i-1}=0$
just because
$E_{2}^{p-2,n-i+1}=E_{2}^{p+2,n-i-1}=0$
just because
![]() $e(E_{2}^{p-2,n-i+1})=\unicode[STIX]{x1D706}_{p-2,i-1}(R/I)$
and
$e(E_{2}^{p-2,n-i+1})=\unicode[STIX]{x1D706}_{p-2,i-1}(R/I)$
and
![]() $e(E_{2}^{p+2,n-i-1})=\unicode[STIX]{x1D706}_{p+2,i+1}(R/I)$
concern
$e(E_{2}^{p+2,n-i-1})=\unicode[STIX]{x1D706}_{p+2,i+1}(R/I)$
concern
![]() $\unicode[STIX]{x1D70C}_{j+1}(R/I)$
and
$\unicode[STIX]{x1D70C}_{j+1}(R/I)$
and
![]() $\unicode[STIX]{x1D70C}_{j-1}(R/I)$
, respectively. Therefore,
$\unicode[STIX]{x1D70C}_{j-1}(R/I)$
, respectively. Therefore,
![]() $d_{2}=d_{2}^{\prime }=0$
is satisfied trivially. When
$d_{2}=d_{2}^{\prime }=0$
is satisfied trivially. When
![]() $j=1$
, that is, the case when
$j=1$
, that is, the case when
![]() $(p+2,n-i-1)=(d,n-d)$
, we have
$(p+2,n-i-1)=(d,n-d)$
, we have
The triviality of
![]() $\unicode[STIX]{x1D70C}_{2}(R/I)$
and
$\unicode[STIX]{x1D70C}_{2}(R/I)$
and
![]() $\unicode[STIX]{x1D70C}_{0}(R/I)$
means that
$\unicode[STIX]{x1D70C}_{0}(R/I)$
means that
![]() $E_{2}^{d-4,n-d+2}=0$
and
$E_{2}^{d-4,n-d+2}=0$
and
![]() $\unicode[STIX]{x1D706}_{d,d}=e(E_{2}^{d,n-d})=1$
, so
$\unicode[STIX]{x1D706}_{d,d}=e(E_{2}^{d,n-d})=1$
, so
![]() $d_{2}=0$
. Now, we assume that the map
$d_{2}=0$
. Now, we assume that the map
![]() $d_{2}^{\prime }:E_{2}^{d-2,n-d+1}\rightarrow E_{2}^{d,n-d}$
is nonzero. Then,
$d_{2}^{\prime }:E_{2}^{d-2,n-d+1}\rightarrow E_{2}^{d,n-d}$
is nonzero. Then,
![]() $\text{Im }d_{2}^{\prime }=E_{2}^{d,n-d}$
due to the fact that
$\text{Im }d_{2}^{\prime }=E_{2}^{d,n-d}$
due to the fact that
![]() $E_{2}^{d,n-d}$
is a simple
$E_{2}^{d,n-d}$
is a simple
![]() $D_{R|k}$
-module. It follows that
$D_{R|k}$
-module. It follows that
![]() $E_{3}^{d,n-d}=E_{2}^{d,n-d}/\text{Im }d_{2}^{\prime }=0$
, so
$E_{3}^{d,n-d}=E_{2}^{d,n-d}/\text{Im }d_{2}^{\prime }=0$
, so
On the other hand, since
![]() $\unicode[STIX]{x1D70C}_{0}(R/I)$
is trivial, we have
$\unicode[STIX]{x1D70C}_{0}(R/I)$
is trivial, we have
for all
![]() $i<d$
. Therefore, we get a contradiction since, by the general theory of spectral sequences, there exists a filtration
$i<d$
. Therefore, we get a contradiction since, by the general theory of spectral sequences, there exists a filtration
where
![]() $E_{\infty }^{i,n-i}={\mathcal{F}}_{i}^{n}/{\mathcal{F}}_{i+1}^{n}$
.
$E_{\infty }^{i,n-i}={\mathcal{F}}_{i}^{n}/{\mathcal{F}}_{i+1}^{n}$
.
Anyway, we have shown that
![]() $d_{2}=d_{2}^{\prime }=0$
in all cases, and this implies that
$d_{2}=d_{2}^{\prime }=0$
in all cases, and this implies that
![]() $E_{3}^{p,n-i}=E_{2}^{p,n-i}\neq 0$
. Now, we consider the maps on
$E_{3}^{p,n-i}=E_{2}^{p,n-i}\neq 0$
. Now, we consider the maps on
![]() $E_{3}$
-terms,
$E_{3}$
-terms,
Since
![]() $E_{3}^{p-3,n-i+2}$
and
$E_{3}^{p-3,n-i+2}$
and
![]() $E_{3}^{p+3,n-i-2}$
concern
$E_{3}^{p+3,n-i-2}$
concern
![]() $\unicode[STIX]{x1D70C}_{j+1}(R/I)$
and
$\unicode[STIX]{x1D70C}_{j+1}(R/I)$
and
![]() $\unicode[STIX]{x1D70C}_{j-1}(R/I)$
, respectively, we have
$\unicode[STIX]{x1D70C}_{j-1}(R/I)$
, respectively, we have
![]() $d_{3}=d_{3}^{\prime }=0$
by the same argument as above. Hence, we have
$d_{3}=d_{3}^{\prime }=0$
by the same argument as above. Hence, we have
![]() $E_{4}^{p,n-i}=E_{3}^{p,n-i}\neq 0$
. Repeating this argument, we have
$E_{4}^{p,n-i}=E_{3}^{p,n-i}\neq 0$
. Repeating this argument, we have
![]() $0\neq E_{2}^{p,n-i}=E_{3}^{p,n-i}=\cdots =E_{\infty }^{p,n-i}$
, so we get a contradiction with the fact that
$0\neq E_{2}^{p,n-i}=E_{3}^{p,n-i}=\cdots =E_{\infty }^{p,n-i}$
, so we get a contradiction with the fact that
![]() $H_{\mathfrak{m}}^{p+n-i}(R)=0$
. (Recall that
$H_{\mathfrak{m}}^{p+n-i}(R)=0$
. (Recall that
![]() $j=i-p\neq 0$
.)◻
$j=i-p\neq 0$
.)◻
The behavior of the consecutive superdiagonals is reflected in the following example.
Example 2.2. Let
![]() $I\subseteq R=\Bbbk [\![x_{1},\ldots ,x_{8}]\!]$
be the Alexander dual ideal of the edge ideal of an
$I\subseteq R=\Bbbk [\![x_{1},\ldots ,x_{8}]\!]$
be the Alexander dual ideal of the edge ideal of an
![]() $8$
-cycle; that is,
$8$
-cycle; that is,
![]() $I^{\vee }=(x_{1}x_{2},x_{2}x_{3},\ldots ,x_{7}x_{8},x_{8}x_{1}).$
Using the results of [Reference Àlvarez Montaner and Vahidi1], we get the Lyubeznik table
$I^{\vee }=(x_{1}x_{2},x_{2}x_{3},\ldots ,x_{7}x_{8},x_{8}x_{1}).$
Using the results of [Reference Àlvarez Montaner and Vahidi1], we get the Lyubeznik table
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(R/I)=\left(\begin{array}{@{}ccccccc@{}}0 & 0 & 0 & 0 & 1 & 0 & 0\\ & 0 & 0 & 0 & 0 & 0 & 0\\ & & 0 & 0 & 0 & 1 & 0\\ & & & 0 & 0 & 1 & 0\\ & & & & 0 & 0 & 0\\ & & & & & 0 & 1\\ & & & & & & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(R/I)=\left(\begin{array}{@{}ccccccc@{}}0 & 0 & 0 & 0 & 1 & 0 & 0\\ & 0 & 0 & 0 & 0 & 0 & 0\\ & & 0 & 0 & 0 & 1 & 0\\ & & & 0 & 0 & 1 & 0\\ & & & & 0 & 0 & 0\\ & & & & & 0 & 1\\ & & & & & & 1\end{array}\right).\end{eqnarray}$$
Notice that
![]() $\unicode[STIX]{x1D70C}_{0}(R/I)$
being trivial does not imply that
$\unicode[STIX]{x1D70C}_{0}(R/I)$
being trivial does not imply that
![]() $\unicode[STIX]{x1D70C}_{1}(R/I)=0$
.
$\unicode[STIX]{x1D70C}_{1}(R/I)=0$
.
Remark 2.3. Using similar spectral sequence arguments to those considered in Theorem 2.1, Kawasaki [Reference Kawasaki12] and Walther [Reference Walther24] described the possible Lyubeznik tables for rings up to dimension two. Namely, their result is as follows.
∙ If
 $d=2$
, then
$d=2$
, then
 $\unicode[STIX]{x1D706}_{2,2}(R/I)-1=\unicode[STIX]{x1D706}_{0,1}(R/I)$
, and the other Lyubeznik numbers are 0.
$\unicode[STIX]{x1D706}_{2,2}(R/I)-1=\unicode[STIX]{x1D706}_{0,1}(R/I)$
, and the other Lyubeznik numbers are 0.
If we take a careful look at the spectral sequence we can also obtain the following.
∙ If
 $d\geqslant 3$
, then
$d\geqslant 3$
, then
 $\unicode[STIX]{x1D706}_{2,d}(R/I)=\unicode[STIX]{x1D706}_{0,d-1}(R/I)$
, and For
$\unicode[STIX]{x1D706}_{2,d}(R/I)=\unicode[STIX]{x1D706}_{0,d-1}(R/I)$
, and For $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{1,d-1}(R/I)\leqslant \unicode[STIX]{x1D706}_{3,d}(R/I) & {\leqslant} & \displaystyle \unicode[STIX]{x1D706}_{1,d-1}(R/I)+\unicode[STIX]{x1D706}_{0,d-2}(R/I)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D706}_{3,d}(R/I)+\unicode[STIX]{x1D706}_{2,d-1}(R/I).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{1,d-1}(R/I)\leqslant \unicode[STIX]{x1D706}_{3,d}(R/I) & {\leqslant} & \displaystyle \unicode[STIX]{x1D706}_{1,d-1}(R/I)+\unicode[STIX]{x1D706}_{0,d-2}(R/I)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D706}_{3,d}(R/I)+\unicode[STIX]{x1D706}_{2,d-1}(R/I).\nonumber\end{eqnarray}$$
 $d=3$
, we can refine the last inequality; that is,
$d=3$
, we can refine the last inequality; that is,  $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1,2}(R/I)+\unicode[STIX]{x1D706}_{0,1}(R/I)=\unicode[STIX]{x1D706}_{3,3}(R/I)+\unicode[STIX]{x1D706}_{2,2}(R/I)-1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1,2}(R/I)+\unicode[STIX]{x1D706}_{0,1}(R/I)=\unicode[STIX]{x1D706}_{3,3}(R/I)+\unicode[STIX]{x1D706}_{2,2}(R/I)-1.\end{eqnarray}$$
Indeed, using the filtration (2.1), we have
Then, the result follows considering the differentials
![]() $d_{2}:E_{2}^{0,n-d+1}\longrightarrow E_{2}^{2,n-d}$
,
$d_{2}:E_{2}^{0,n-d+1}\longrightarrow E_{2}^{2,n-d}$
,
![]() $d_{2}:E_{2}^{1,n-d+1}\longrightarrow E_{2}^{3,n-d}$
,
$d_{2}:E_{2}^{1,n-d+1}\longrightarrow E_{2}^{3,n-d}$
,
![]() $d_{2}:E_{2}^{0,n-d+2}\longrightarrow E_{2}^{2,n-d+1}$
and
$d_{2}:E_{2}^{0,n-d+2}\longrightarrow E_{2}^{2,n-d+1}$
and
![]() $d_{3}:E_{3}^{0,n-d+2}\longrightarrow E_{3}^{3,n-d}$
. Finally, we point out that
$d_{3}:E_{3}^{0,n-d+2}\longrightarrow E_{3}^{3,n-d}$
. Finally, we point out that
![]() $E_{3}^{0,n-d+1}=E_{\infty }^{0,n-d+1}$
,
$E_{3}^{0,n-d+1}=E_{\infty }^{0,n-d+1}$
,
![]() $E_{3}^{1,n-d+1}=E_{\infty }^{1,n-d+1}$
,
$E_{3}^{1,n-d+1}=E_{\infty }^{1,n-d+1}$
,
![]() $E_{3}^{2,n-d}=E_{\infty }^{2,n-d}$
,
$E_{3}^{2,n-d}=E_{\infty }^{2,n-d}$
,
![]() $E_{4}^{0,n-d+2}=E_{\infty }^{0,n-d+2}$
and
$E_{4}^{0,n-d+2}=E_{\infty }^{0,n-d+2}$
and
![]() $E_{4}^{3,n-d}=E_{\infty }^{3,n-d}$
.
$E_{4}^{3,n-d}=E_{\infty }^{3,n-d}$
.
3 Linear strands of minimal free resolutions of
 $\mathbb{Z}$
-graded ideals
$\mathbb{Z}$
-graded ideals
Throughout this section, we consider
![]() $\mathbb{Z}$
-graded ideals
$\mathbb{Z}$
-graded ideals
![]() $I$
in the polynomial ring
$I$
in the polynomial ring
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
. In particular,
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
. In particular,
![]() $I$
is not necessarily a monomial ideal. For simplicity, we assume that
$I$
is not necessarily a monomial ideal. For simplicity, we assume that
![]() $I\neq 0$
. The minimal
$I\neq 0$
. The minimal
![]() $\mathbb{Z}$
-graded free resolution of
$\mathbb{Z}$
-graded free resolution of
![]() $I$
is an exact sequence of free
$I$
is an exact sequence of free
![]() $\mathbb{Z}$
-graded modules:
$\mathbb{Z}$
-graded modules:
where the
![]() $i$
th term is of the form
$i$
th term is of the form
and the matrices of the morphisms
![]() $d_{i}:L_{i}\longrightarrow L_{i-1}$
do not contain invertible elements. The Betti numbers of
$d_{i}:L_{i}\longrightarrow L_{i-1}$
do not contain invertible elements. The Betti numbers of
![]() $I$
are the invariants
$I$
are the invariants
![]() $\unicode[STIX]{x1D6FD}_{i,j}(I)$
. Notice that
$\unicode[STIX]{x1D6FD}_{i,j}(I)$
. Notice that
![]() $L_{i}\cong R^{\unicode[STIX]{x1D6FD}_{i}(I)}$
as underlying
$L_{i}\cong R^{\unicode[STIX]{x1D6FD}_{i}(I)}$
as underlying
![]() $R$
-modules, where, for each
$R$
-modules, where, for each
![]() $i$
, we set
$i$
, we set
![]() $\unicode[STIX]{x1D6FD}_{i}(I):=\sum _{j\in \mathbb{Z}}\unicode[STIX]{x1D6FD}_{i,j}(I)$
. Hence, (3.1) implies that
$\unicode[STIX]{x1D6FD}_{i}(I):=\sum _{j\in \mathbb{Z}}\unicode[STIX]{x1D6FD}_{i,j}(I)$
. Hence, (3.1) implies that
Given
![]() $r\in \mathbb{N}$
, we also consider the
$r\in \mathbb{N}$
, we also consider the
![]() $r$
-linear strand of
$r$
-linear strand of
![]() $L_{\bullet }(I)$
:
$L_{\bullet }(I)$
:
where
and the differential
![]() $d_{i}^{{<}r>}:L_{i}^{{<}r>}\longrightarrow L_{i-1}^{{<}r>}$
is the corresponding component of
$d_{i}^{{<}r>}:L_{i}^{{<}r>}\longrightarrow L_{i-1}^{{<}r>}$
is the corresponding component of
![]() $d_{i}$
.
$d_{i}$
.
Remark 3.1. Sometimes, we also consider the minimal
![]() $\mathbb{Z}$
-graded free resolution
$\mathbb{Z}$
-graded free resolution
![]() $L_{\bullet }(R/I)$
of the quotient ring
$L_{\bullet }(R/I)$
of the quotient ring
![]() $R/I$
:
$R/I$
:
Its truncation at the first term
![]() $L_{{\geqslant}1}(R/I)$
gives a minimal free resolution
$L_{{\geqslant}1}(R/I)$
gives a minimal free resolution
![]() $L_{\bullet }(I)$
of
$L_{\bullet }(I)$
of
![]() $I$
. For
$I$
. For
![]() $r\geqslant 2$
,
$r\geqslant 2$
,
![]() $\mathbb{L}_{\bullet }^{{<}r>}(I)$
is isomorphic to the
$\mathbb{L}_{\bullet }^{{<}r>}(I)$
is isomorphic to the
![]() $(r-1)$
-linear strand
$(r-1)$
-linear strand
![]() $\mathbb{L}_{\bullet }^{{<}r-1>}(R/I)$
up to translation. However, this is not true for
$\mathbb{L}_{\bullet }^{{<}r-1>}(R/I)$
up to translation. However, this is not true for
![]() $r=1$
, since
$r=1$
, since
![]() $\mathbb{L}_{\bullet }^{{<}0>}(R/I)$
starts from the
$\mathbb{L}_{\bullet }^{{<}0>}(R/I)$
starts from the
![]() $0$
th term
$0$
th term
![]() $R$
, which is irrelevant to
$R$
, which is irrelevant to
![]() $\mathbb{L}_{\bullet }^{{<}1>}(I)$
.
$\mathbb{L}_{\bullet }^{{<}1>}(I)$
.
To the minimal
![]() $\mathbb{Z}$
-graded free resolution of
$\mathbb{Z}$
-graded free resolution of
![]() $I$
we may associate a set of invariants that measure the acyclicity of the linear strands as follows. Let
$I$
we may associate a set of invariants that measure the acyclicity of the linear strands as follows. Let
![]() $\mathbb{K}$
denote the field of fractions
$\mathbb{K}$
denote the field of fractions
![]() $Q(R)$
of
$Q(R)$
of
![]() $R$
, and set
$R$
, and set
Since the complex
![]() $\mathbb{L}_{\bullet }^{{<}r>}(I)\otimes _{R}\mathbb{K}$
is of the form
$\mathbb{L}_{\bullet }^{{<}r>}(I)\otimes _{R}\mathbb{K}$
is of the form
we have
![]() $\unicode[STIX]{x1D708}_{i,j}(I)\leqslant \unicode[STIX]{x1D6FD}_{i,j}(I)$
for all
$\unicode[STIX]{x1D708}_{i,j}(I)\leqslant \unicode[STIX]{x1D6FD}_{i,j}(I)$
for all
![]() $i,j$
(if
$i,j$
(if
![]() $i>j$
then
$i>j$
then
![]() $\unicode[STIX]{x1D708}_{i,j}(I)=\unicode[STIX]{x1D6FD}_{i,j}(I)=0$
), and
$\unicode[STIX]{x1D708}_{i,j}(I)=\unicode[STIX]{x1D6FD}_{i,j}(I)=0$
), and
for each
![]() $r$
. If we mimic the construction of the Betti table, we may also consider the
$r$
. If we mimic the construction of the Betti table, we may also consider the
![]() $\unicode[STIX]{x1D708}$
-table of
$\unicode[STIX]{x1D708}$
-table of
![]() $I$
:
$I$
:

Next, we consider some basic properties of
![]() $\unicode[STIX]{x1D708}$
-numbers. It turns out that they satisfy analogous properties to those of Lyubeznik numbers. For instance, these invariants satisfy the following Euler characteristic formula.
$\unicode[STIX]{x1D708}$
-numbers. It turns out that they satisfy analogous properties to those of Lyubeznik numbers. For instance, these invariants satisfy the following Euler characteristic formula.
Lemma 3.2. For a
![]() $\mathbb{Z}$
-graded ideal
$\mathbb{Z}$
-graded ideal
![]() $I$
, we have
$I$
, we have
Proof. The assertion follows from the computation below:
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i,j\in \mathbb{N}}(-1)^{i}\unicode[STIX]{x1D708}_{i,j}(I) & = & \displaystyle \mathop{\sum }_{i,r\in \mathbb{N}}(-1)^{i}\unicode[STIX]{x1D708}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r\in \mathbb{N}}\mathop{\sum }_{0\leqslant i\leqslant n}(-1)^{i}\unicode[STIX]{x1D708}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r\in \mathbb{N}}\mathop{\sum }_{0\leqslant i\leqslant n}(-1)^{i}\unicode[STIX]{x1D6FD}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\leqslant i\leqslant n}\mathop{\sum }_{r\in \mathbb{N}}(-1)^{i}\unicode[STIX]{x1D6FD}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\leqslant i\leqslant n}(-1)^{i}\unicode[STIX]{x1D6FD}_{i}(I)\nonumber\\ \displaystyle & = & \displaystyle 1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i,j\in \mathbb{N}}(-1)^{i}\unicode[STIX]{x1D708}_{i,j}(I) & = & \displaystyle \mathop{\sum }_{i,r\in \mathbb{N}}(-1)^{i}\unicode[STIX]{x1D708}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r\in \mathbb{N}}\mathop{\sum }_{0\leqslant i\leqslant n}(-1)^{i}\unicode[STIX]{x1D708}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{r\in \mathbb{N}}\mathop{\sum }_{0\leqslant i\leqslant n}(-1)^{i}\unicode[STIX]{x1D6FD}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\leqslant i\leqslant n}\mathop{\sum }_{r\in \mathbb{N}}(-1)^{i}\unicode[STIX]{x1D6FD}_{i,i+r}(I)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\leqslant i\leqslant n}(-1)^{i}\unicode[STIX]{x1D6FD}_{i}(I)\nonumber\\ \displaystyle & = & \displaystyle 1.\nonumber\end{eqnarray}$$
We can also single out a particular nonvanishing
![]() $\unicode[STIX]{x1D708}$
-number. For each
$\unicode[STIX]{x1D708}$
-number. For each
![]() $i\in \mathbb{N}$
, let
$i\in \mathbb{N}$
, let
![]() $I_{{<}i>}$
denote the ideal generated by the homogeneous component
$I_{{<}i>}$
denote the ideal generated by the homogeneous component
![]() $I_{i}=\{f\in I\mid \deg (f)=i\}\cup \{0\}$
. Then, we have the following.
$I_{i}=\{f\in I\mid \deg (f)=i\}\cup \{0\}$
. Then, we have the following.
Lemma 3.3. If
![]() $I$
is a
$I$
is a
![]() $\mathbb{Z}$
-graded ideal with
$\mathbb{Z}$
-graded ideal with
![]() $l:=\min \{i\mid I_{i}\neq 0\}$
, then we have
$l:=\min \{i\mid I_{i}\neq 0\}$
, then we have
![]() $\unicode[STIX]{x1D708}_{0,l}(I)\neq 0$
.
$\unicode[STIX]{x1D708}_{0,l}(I)\neq 0$
.
Proof. It is easy to see that there is a surjection
![]() $H_{0}(\mathbb{L}_{\bullet }^{{<}l>}(I)){\twoheadrightarrow}I_{{<}l>}$
. Since
$H_{0}(\mathbb{L}_{\bullet }^{{<}l>}(I)){\twoheadrightarrow}I_{{<}l>}$
. Since
![]() $\dim _{R}I_{{<}l>}=n$
, we have
$\dim _{R}I_{{<}l>}=n$
, we have
![]() $H_{0}(\mathbb{L}_{\bullet }^{{<}l>}(I)\otimes _{R}\mathbb{K})\cong H_{0}(\mathbb{L}_{\bullet }^{{<}l>}\,(I))\otimes _{R}\mathbb{K}\neq 0$
.◻
$H_{0}(\mathbb{L}_{\bullet }^{{<}l>}(I)\otimes _{R}\mathbb{K})\cong H_{0}(\mathbb{L}_{\bullet }^{{<}l>}\,(I))\otimes _{R}\mathbb{K}\neq 0$
.◻
This fact allows us to consider the following notion.
Definition 3.4. Let
![]() $I$
be a
$I$
be a
![]() $\mathbb{Z}$
-graded ideal, and set
$\mathbb{Z}$
-graded ideal, and set
![]() $l:=\min \{i\mid I_{i}\neq 0\}$
. We say that
$l:=\min \{i\mid I_{i}\neq 0\}$
. We say that
![]() $I$
has a trivial
$I$
has a trivial
![]() $\unicode[STIX]{x1D708}$
-table if
$\unicode[STIX]{x1D708}$
-table if
![]() $\unicode[STIX]{x1D708}_{0,l}(I)=1$
and the rest of these invariants vanish.
$\unicode[STIX]{x1D708}_{0,l}(I)=1$
and the rest of these invariants vanish.
3.1 Componentwise linear ideals
It might be an interesting problem to find necessary and/or sufficient conditions for a
![]() $\mathbb{Z}$
-graded ideal to have a trivial
$\mathbb{Z}$
-graded ideal to have a trivial
![]() $\unicode[STIX]{x1D708}$
-table. In this direction, we have the following relation to the notion of componentwise linear ideals.
$\unicode[STIX]{x1D708}$
-table. In this direction, we have the following relation to the notion of componentwise linear ideals.
Definition 3.5. (Herzog and Hibi [Reference Herzog and Hibi8])
We say that a
![]() $\mathbb{Z}$
-graded ideal
$\mathbb{Z}$
-graded ideal
![]() $I$
is componentwise linear if
$I$
is componentwise linear if
![]() $I_{{<}r>}$
has a linear resolution for all
$I_{{<}r>}$
has a linear resolution for all
![]() $r\in \mathbb{N}$
; that is,
$r\in \mathbb{N}$
; that is,
![]() $\unicode[STIX]{x1D6FD}_{i,j}(I_{{<}r>})=0$
unless
$\unicode[STIX]{x1D6FD}_{i,j}(I_{{<}r>})=0$
unless
![]() $j=i+r$
.
$j=i+r$
.
Römer [Reference Römer20] and the second author [Reference Yanagawa25, Theorem 4.1] independently showed that
![]() $I$
is componentwise linear if and only if
$I$
is componentwise linear if and only if
![]() $H_{i}(\mathbb{L}_{\bullet }^{{<}r>}(I))=0$
for all
$H_{i}(\mathbb{L}_{\bullet }^{{<}r>}(I))=0$
for all
![]() $r$
and all
$r$
and all
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
Proposition 3.6. A componentwise linear ideal
![]() $I$
has a trivial
$I$
has a trivial
![]() $\unicode[STIX]{x1D708}$
-table.
$\unicode[STIX]{x1D708}$
-table.
Proof. Since
![]() $I$
is componentwise linear, we have
$I$
is componentwise linear, we have
![]() $H_{i}(\mathbb{L}_{\bullet }^{{<}r>}(I))=0$
for all
$H_{i}(\mathbb{L}_{\bullet }^{{<}r>}(I))=0$
for all
![]() $r$
and all
$r$
and all
![]() $i\geqslant 1$
, and hence
$i\geqslant 1$
, and hence
![]() $\unicode[STIX]{x1D708}_{i,j}(I)=0$
for all
$\unicode[STIX]{x1D708}_{i,j}(I)=0$
for all
![]() $j$
and all
$j$
and all
![]() $i\geqslant 1$
. Now, the assertion follows from Lemmas 3.2 and 3.3.◻
$i\geqslant 1$
. Now, the assertion follows from Lemmas 3.2 and 3.3.◻
The converse of the above proposition is not true. For example, in Corollary 3.13 below, we show that if
![]() $I_{1}\neq 0$
, then it has a trivial
$I_{1}\neq 0$
, then it has a trivial
![]() $\unicode[STIX]{x1D708}$
-table. However, there is no relation between being componentwise linear and
$\unicode[STIX]{x1D708}$
-table. However, there is no relation between being componentwise linear and
![]() $I_{1}\neq 0$
.
$I_{1}\neq 0$
.
3.2 Consecutiveness of nontrivial columns of the
 $\unicode[STIX]{x1D708}$
-tables
$\unicode[STIX]{x1D708}$
-tables
For a
![]() $\mathbb{Z}$
-graded ideal
$\mathbb{Z}$
-graded ideal
![]() $I\subseteq R$
and
$I\subseteq R$
and
![]() $i\in \mathbb{N}$
, set
$i\in \mathbb{N}$
, set
If we denote
![]() $\mathbb{L}_{\bullet }(I):=\bigoplus _{r\in \mathbb{N}}\mathbb{L}_{\bullet }^{{<}r>}(I)$
, then
$\mathbb{L}_{\bullet }(I):=\bigoplus _{r\in \mathbb{N}}\mathbb{L}_{\bullet }^{{<}r>}(I)$
, then
By Lemma 3.2, we have
![]() $\sum _{i=0}^{n}(-1)^{i}\unicode[STIX]{x1D708}_{i}(I)=1$
. We say that
$\sum _{i=0}^{n}(-1)^{i}\unicode[STIX]{x1D708}_{i}(I)=1$
. We say that
![]() $\unicode[STIX]{x1D708}_{i}(I)$
is nontrivial if
$\unicode[STIX]{x1D708}_{i}(I)$
is nontrivial if
Clearly, the
![]() $\unicode[STIX]{x1D708}$
-table of
$\unicode[STIX]{x1D708}$
-table of
![]() $I$
is nontrivial if and only if
$I$
is nontrivial if and only if
![]() $\unicode[STIX]{x1D708}_{i}(I)$
is nontrivial for some
$\unicode[STIX]{x1D708}_{i}(I)$
is nontrivial for some
![]() $i$
. If
$i$
. If
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
![]() $\text{proj.dim}_{R}I\leqslant n-1$
, and hence
$\text{proj.dim}_{R}I\leqslant n-1$
, and hence
![]() $\unicode[STIX]{x1D708}_{n}(I)=0$
. In particular,
$\unicode[STIX]{x1D708}_{n}(I)=0$
. In particular,
![]() $\unicode[STIX]{x1D708}_{n}(I)$
is always trivial.
$\unicode[STIX]{x1D708}_{n}(I)$
is always trivial.
The main result of this subsection is the following.
Theorem 3.7. Let
![]() $I$
be a
$I$
be a
![]() $\mathbb{Z}$
-graded ideal of
$\mathbb{Z}$
-graded ideal of
![]() $R$
. Then, we have the following.
$R$
. Then, we have the following.
∙ If
 $\unicode[STIX]{x1D708}_{j}(I)$
is nontrivial for
$\unicode[STIX]{x1D708}_{j}(I)$
is nontrivial for
 $1\leqslant j\leqslant n-1$
, then either
$1\leqslant j\leqslant n-1$
, then either
 $\unicode[STIX]{x1D708}_{j-1}(I)$
or
$\unicode[STIX]{x1D708}_{j-1}(I)$
or
 $\unicode[STIX]{x1D708}_{j+1}(I)$
is nontrivial.
$\unicode[STIX]{x1D708}_{j+1}(I)$
is nontrivial.∙ If
 $\unicode[STIX]{x1D708}_{0}(I)$
is nontrivial, then so is
$\unicode[STIX]{x1D708}_{0}(I)$
is nontrivial, then so is
 $\unicode[STIX]{x1D708}_{1}(I)$
.
$\unicode[STIX]{x1D708}_{1}(I)$
.
In order to prove the theorem, we reconstruct
![]() $\mathbb{L}_{\bullet }(I)$
using a spectral sequence. Let
$\mathbb{L}_{\bullet }(I)$
using a spectral sequence. Let
![]() $L_{\bullet }(I)$
be the minimal free resolution of
$L_{\bullet }(I)$
be the minimal free resolution of
![]() $I$
as before. Consider the
$I$
as before. Consider the
![]() $\mathfrak{m}$
-adic filtration
$\mathfrak{m}$
-adic filtration
![]() $L_{\bullet }(I)=F_{0}L_{\bullet }\supset F_{1}L_{\bullet }\supset \cdots \,$
of
$L_{\bullet }(I)=F_{0}L_{\bullet }\supset F_{1}L_{\bullet }\supset \cdots \,$
of
![]() $L_{\bullet }(I)$
, where
$L_{\bullet }(I)$
, where
![]() $F_{i}L_{\bullet }$
is a subcomplex whose component of homological degree
$F_{i}L_{\bullet }$
is a subcomplex whose component of homological degree
![]() $j$
is
$j$
is
![]() $\mathfrak{m}^{i}L_{j}$
. For any given
$\mathfrak{m}^{i}L_{j}$
. For any given
![]() $R$
-module
$R$
-module
![]() $M$
, we regard
$M$
, we regard
![]() $\text{gr}\,(M):=\bigoplus _{i\in \mathbb{N}}\mathfrak{m}^{i}M/\mathfrak{m}^{i+1}M$
as an
$\text{gr}\,(M):=\bigoplus _{i\in \mathbb{N}}\mathfrak{m}^{i}M/\mathfrak{m}^{i+1}M$
as an
![]() $R$
-module via the isomorphism
$R$
-module via the isomorphism
![]() $\text{gr}\,R=\bigoplus _{i\in \mathbb{N}}\mathfrak{m}^{i}/\mathfrak{m}^{i+1}\cong R=\Bbbk [x_{1},\ldots ,x_{n}]$
. Since each
$\text{gr}\,R=\bigoplus _{i\in \mathbb{N}}\mathfrak{m}^{i}/\mathfrak{m}^{i+1}\cong R=\Bbbk [x_{1},\ldots ,x_{n}]$
. Since each
![]() $L_{j}$
is a free
$L_{j}$
is a free
![]() $R$
-module,
$R$
-module,
 $$\begin{eqnarray}\bigoplus _{p+q=-j}E_{0}^{p,q}=\left(\bigoplus _{p\geqslant 0}\mathfrak{m}^{p}L_{j}/\mathfrak{m}^{p+1}L_{j}\right)=\text{gr}\,L_{j}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{p+q=-j}E_{0}^{p,q}=\left(\bigoplus _{p\geqslant 0}\mathfrak{m}^{p}L_{j}/\mathfrak{m}^{p+1}L_{j}\right)=\text{gr}\,L_{j}\end{eqnarray}$$
is isomorphic to
![]() $L_{j}$
(if we identify
$L_{j}$
(if we identify
![]() $\text{gr}\,R$
with
$\text{gr}\,R$
with
![]() $R$
), while we have to forget the original
$R$
), while we have to forget the original
![]() $\mathbb{Z}$
-grading of
$\mathbb{Z}$
-grading of
![]() $L_{j}$
. Since
$L_{j}$
. Since
![]() $L_{\bullet }(I)$
is a minimal free resolution,
$L_{\bullet }(I)$
is a minimal free resolution,
![]() $d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}$
is the zero map for all
$d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}$
is the zero map for all
![]() $p,q$
, and hence
$p,q$
, and hence
![]() $E_{0}^{p,q}=E_{1}^{p,q}$
. It follows that
$E_{0}^{p,q}=E_{1}^{p,q}$
. It follows that
is isomorphic to
![]() $L_{j}$
under the identification
$L_{j}$
under the identification
![]() $R\cong \text{gr}\,R$
. Collecting the maps
$R\cong \text{gr}\,R$
. Collecting the maps
for
![]() $p,q$
with
$p,q$
with
![]() $p+q=-j$
, we have the
$p+q=-j$
, we have the
![]() $R$
-morphism
$R$
-morphism
![]() $d_{j}^{(1)}:\mathbb{E}_{j}^{(1)}\rightarrow \mathbb{E}_{j-1}^{(1)}$
, and these morphisms make
$d_{j}^{(1)}:\mathbb{E}_{j}^{(1)}\rightarrow \mathbb{E}_{j-1}^{(1)}$
, and these morphisms make
![]() $\mathbb{E}_{\bullet }^{(1)}$
a chain complex of
$\mathbb{E}_{\bullet }^{(1)}$
a chain complex of
![]() $R$
-modules. Under the isomorphism
$R$
-modules. Under the isomorphism
![]() $\mathbb{E}_{j}^{(1)}\cong L_{j}$
,
$\mathbb{E}_{j}^{(1)}\cong L_{j}$
,
![]() $\mathbb{E}_{\bullet }^{(1)}$
is isomorphic to
$\mathbb{E}_{\bullet }^{(1)}$
is isomorphic to
![]() $\mathbb{L}_{\bullet }(I)=\bigoplus _{r\in \mathbb{N}}\mathbb{L}_{\bullet }^{{<}r>}(I)$
. Hence, we have
$\mathbb{L}_{\bullet }(I)=\bigoplus _{r\in \mathbb{N}}\mathbb{L}_{\bullet }^{{<}r>}(I)$
. Hence, we have
and
![]() $\unicode[STIX]{x1D708}_{j}(I)=\dim _{\mathbb{K}}(\mathbb{E}_{j}^{(2)}\otimes _{R}\mathbb{K})$
. Collecting the maps
$\unicode[STIX]{x1D708}_{j}(I)=\dim _{\mathbb{K}}(\mathbb{E}_{j}^{(2)}\otimes _{R}\mathbb{K})$
. Collecting the maps
![]() $d_{2}^{p,q}:E_{2}^{p,q}\rightarrow E_{2}^{p+2,q-1}$
, we have the
$d_{2}^{p,q}:E_{2}^{p,q}\rightarrow E_{2}^{p+2,q-1}$
, we have the
![]() $R$
-morphism
$R$
-morphism
Moreover, we have the chain complex
of
![]() $R$
-modules whose
$R$
-modules whose
![]() $j$
th homology is isomorphic to
$j$
th homology is isomorphic to
![]() $\mathbb{E}_{j}^{(3)}:=\bigoplus _{p+q=-j}E_{3}^{p,q}.$
For all
$\mathbb{E}_{j}^{(3)}:=\bigoplus _{p+q=-j}E_{3}^{p,q}.$
For all
![]() $r\geqslant 4$
,
$r\geqslant 4$
,
![]() $\mathbb{E}_{j}^{(r)}:=\bigoplus _{p+q=-j}E_{r}^{p,q}$
satisfies the same property.
$\mathbb{E}_{j}^{(r)}:=\bigoplus _{p+q=-j}E_{r}^{p,q}$
satisfies the same property.
By the construction of spectral sequences, if
then the map
![]() $d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}$
is zero for all
$d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}$
is zero for all
![]() $p,q$
with
$p,q$
with
![]() $p+q=-j$
, and hence
$p+q=-j$
, and hence
![]() $d_{j}^{(r)}:\mathbb{E}_{j}^{(r)}\rightarrow \mathbb{E}_{j-1}^{(r)}$
is zero. This implies that
$d_{j}^{(r)}:\mathbb{E}_{j}^{(r)}\rightarrow \mathbb{E}_{j-1}^{(r)}$
is zero. This implies that
![]() $\mathbb{E}_{j}^{(r)}$
is isomorphic to
$\mathbb{E}_{j}^{(r)}$
is isomorphic to
for
![]() $r\gg 0$
.
$r\gg 0$
.
Proof of Theorem 3.7.
We prove the assertion by contradiction using the spectral sequence introduced above. First, assume that
![]() $\unicode[STIX]{x1D708}_{j}(I)$
is nontrivial for some
$\unicode[STIX]{x1D708}_{j}(I)$
is nontrivial for some
![]() $2\leqslant j\leqslant n-1$
, but both
$2\leqslant j\leqslant n-1$
, but both
![]() $\unicode[STIX]{x1D708}_{j-1}(I)$
and
$\unicode[STIX]{x1D708}_{j-1}(I)$
and
![]() $\unicode[STIX]{x1D708}_{j+1}(I)$
are trivial. (The cases
$\unicode[STIX]{x1D708}_{j+1}(I)$
are trivial. (The cases
![]() $j=0,1$
can be proved using similar arguments, and we make a few remarks later.) Then, we have
$j=0,1$
can be proved using similar arguments, and we make a few remarks later.) Then, we have
![]() $\mathbb{E}_{j}^{(2)}\otimes _{R}\mathbb{K}\neq 0$
and
$\mathbb{E}_{j}^{(2)}\otimes _{R}\mathbb{K}\neq 0$
and
![]() $\mathbb{E}_{j+1}^{(2)}\otimes _{R}\mathbb{K}=\mathbb{E}_{j-1}^{(2)}\otimes _{R}\mathbb{K}=0.$
It follows that
$\mathbb{E}_{j+1}^{(2)}\otimes _{R}\mathbb{K}=\mathbb{E}_{j-1}^{(2)}\otimes _{R}\mathbb{K}=0.$
It follows that
![]() $\mathbb{E}_{j}^{(3)}\otimes _{R}\mathbb{K}\neq 0,$
since it is the homology of
$\mathbb{E}_{j}^{(3)}\otimes _{R}\mathbb{K}\neq 0,$
since it is the homology of
Similarly, we have
![]() $\mathbb{E}_{j-1}^{(3)}\otimes _{R}\mathbb{K}=\mathbb{E}_{j+1}^{(3)}\otimes _{R}\mathbb{K}=0.$
Repeating this argument, we have
$\mathbb{E}_{j-1}^{(3)}\otimes _{R}\mathbb{K}=\mathbb{E}_{j+1}^{(3)}\otimes _{R}\mathbb{K}=0.$
Repeating this argument, we have
![]() $\mathbb{E}_{j}^{(r)}\otimes _{R}\mathbb{K}\neq 0$
for all
$\mathbb{E}_{j}^{(r)}\otimes _{R}\mathbb{K}\neq 0$
for all
![]() $r\geqslant 4$
. Hence,
$r\geqslant 4$
. Hence,
![]() $E_{\infty }^{p,q}\neq 0$
for some
$E_{\infty }^{p,q}\neq 0$
for some
![]() $p,q$
with
$p,q$
with
![]() $p+q=-j$
. However, this contradicts the facts that
$p+q=-j$
. However, this contradicts the facts that
and
![]() $H_{j}(L_{\bullet }(I))=0$
. (Recall that
$H_{j}(L_{\bullet }(I))=0$
. (Recall that
![]() $j>0$
now.)
$j>0$
now.)
Next, we assume that
![]() $\unicode[STIX]{x1D708}_{1}(I)$
is nontrivial, but
$\unicode[STIX]{x1D708}_{1}(I)$
is nontrivial, but
![]() $\unicode[STIX]{x1D708}_{0}(I)$
and
$\unicode[STIX]{x1D708}_{0}(I)$
and
![]() $\unicode[STIX]{x1D708}_{2}(I)$
are trivial. That is,
$\unicode[STIX]{x1D708}_{2}(I)$
are trivial. That is,
As we have seen above, we must have
![]() $\mathbb{E}_{1}^{(r)}=0$
for
$\mathbb{E}_{1}^{(r)}=0$
for
![]() $r\gg 0$
. Since
$r\gg 0$
. Since
![]() $\mathbb{E}_{2}^{(r)}\otimes _{R}\mathbb{K}=0$
for all
$\mathbb{E}_{2}^{(r)}\otimes _{R}\mathbb{K}=0$
for all
![]() $r$
now, if
$r$
now, if
![]() $d_{1}^{(r)}\otimes _{R}\mathbb{K}:\mathbb{E}_{1}^{(r)}\otimes _{R}\mathbb{K}\longrightarrow \mathbb{E}_{0}^{(r)}\otimes _{R}\mathbb{K}$
are the zero maps for all
$d_{1}^{(r)}\otimes _{R}\mathbb{K}:\mathbb{E}_{1}^{(r)}\otimes _{R}\mathbb{K}\longrightarrow \mathbb{E}_{0}^{(r)}\otimes _{R}\mathbb{K}$
are the zero maps for all
![]() $r$
, then
$r$
, then
![]() $\mathbb{E}_{1}^{(r)}\otimes _{R}\mathbb{K}\cong \mathbb{E}_{1}^{(2)}\otimes _{R}\mathbb{K}\neq 0$
for all
$\mathbb{E}_{1}^{(r)}\otimes _{R}\mathbb{K}\cong \mathbb{E}_{1}^{(2)}\otimes _{R}\mathbb{K}\neq 0$
for all
![]() $r$
, and this is a contradiction. Therefore, there is some
$r$
, and this is a contradiction. Therefore, there is some
![]() $r\geqslant 2$
such that
$r\geqslant 2$
such that
![]() $d_{1}^{(r)}\otimes _{R}\mathbb{K}$
is not zero. If
$d_{1}^{(r)}\otimes _{R}\mathbb{K}$
is not zero. If
![]() $s$
is the minimum among these
$s$
is the minimum among these
![]() $r$
,
$r$
,
![]() $d_{1}^{(s)}\otimes _{R}\mathbb{K}:\mathbb{E}_{1}^{(s)}\otimes _{R}\mathbb{K}\longrightarrow (\mathbb{E}_{0}^{(s)}\otimes _{R}\mathbb{K})\cong \mathbb{K}$
is surjective. Hence,
$d_{1}^{(s)}\otimes _{R}\mathbb{K}:\mathbb{E}_{1}^{(s)}\otimes _{R}\mathbb{K}\longrightarrow (\mathbb{E}_{0}^{(s)}\otimes _{R}\mathbb{K})\cong \mathbb{K}$
is surjective. Hence,
![]() $\mathbb{E}_{0}^{(r)}\otimes _{R}\mathbb{K}=0$
for all
$\mathbb{E}_{0}^{(r)}\otimes _{R}\mathbb{K}=0$
for all
![]() $r>s$
, and
$r>s$
, and
![]() $\mathbb{E}_{0}^{(\infty )}\otimes _{R}\mathbb{K}=0$
. However, since
$\mathbb{E}_{0}^{(\infty )}\otimes _{R}\mathbb{K}=0$
. However, since
![]() $\mathbb{E}_{0}^{(\infty )}\cong \text{gr}\,H_{0}(L_{\bullet }(I))\cong \text{gr}\,(I)$
and
$\mathbb{E}_{0}^{(\infty )}\cong \text{gr}\,H_{0}(L_{\bullet }(I))\cong \text{gr}\,(I)$
and
![]() $\dim _{R}I=n$
, we have
$\dim _{R}I=n$
, we have
![]() $\dim _{R}(\text{gr}\,(I))=n$
and hence
$\dim _{R}(\text{gr}\,(I))=n$
and hence
![]() $\mathbb{E}_{0}^{(\infty )}\otimes _{R}\mathbb{K}\neq 0$
. This is a contradiction. The case when
$\mathbb{E}_{0}^{(\infty )}\otimes _{R}\mathbb{K}\neq 0$
. This is a contradiction. The case when
![]() $\unicode[STIX]{x1D708}_{0}(I)$
is nontrivial can be proved in a similar way.◻
$\unicode[STIX]{x1D708}_{0}(I)$
is nontrivial can be proved in a similar way.◻
3.3 Thom–Sebastiani type formulas
Let
![]() $I,J$
be
$I,J$
be
![]() $\mathbb{Z}$
-graded ideals in two disjoint sets of variables, say
$\mathbb{Z}$
-graded ideals in two disjoint sets of variables, say
![]() $I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
$I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
![]() $J\subseteq S=\Bbbk [y_{1},\ldots ,y_{n}]$
. The aim of this subsection is to describe the
$J\subseteq S=\Bbbk [y_{1},\ldots ,y_{n}]$
. The aim of this subsection is to describe the
![]() $\unicode[STIX]{x1D708}$
-numbers of
$\unicode[STIX]{x1D708}$
-numbers of
![]() $IT+JT$
, where
$IT+JT$
, where
![]() $T=R\otimes _{\Bbbk }S=\Bbbk [x_{1},\ldots ,x_{m},y_{1},\ldots ,y_{n}]$
, in terms of those of
$T=R\otimes _{\Bbbk }S=\Bbbk [x_{1},\ldots ,x_{m},y_{1},\ldots ,y_{n}]$
, in terms of those of
![]() $I$
and
$I$
and
![]() $J$
, respectively. When we just consider Betti numbers, we have the following results due to Jacques and Katzman [Reference Jacques and Katzman11].
$J$
, respectively. When we just consider Betti numbers, we have the following results due to Jacques and Katzman [Reference Jacques and Katzman11].
Proposition 3.8. (Cf. [Reference Jacques and Katzman11, Lemma 2.1])
Let
![]() $L_{\bullet }(R/I)$
and
$L_{\bullet }(R/I)$
and
![]() $L_{\bullet }(S/J)$
be minimal graded free resolutions of
$L_{\bullet }(S/J)$
be minimal graded free resolutions of
![]() $R/I$
and
$R/I$
and
![]() $S/J$
, respectively. Then,
$S/J$
, respectively. Then,
is a minimal graded free resolution of
![]() $T/IT+JT$
.
$T/IT+JT$
.
Hence, Betti numbers satisfy the following relation.
Corollary 3.9. (Cf. [Reference Jacques and Katzman11, Corollary 2.2])
The Betti numbers of
![]() $T/IT+JT$
have the following form:
$T/IT+JT$
have the following form:
Hence, we have
Our aim is to extend the result in [Reference Jacques and Katzman11] to the case of
![]() $\unicode[STIX]{x1D708}$
-numbers. To such purpose, it is more convenient to consider separately the case of ideals with degree one elements. Thus, let
$\unicode[STIX]{x1D708}$
-numbers. To such purpose, it is more convenient to consider separately the case of ideals with degree one elements. Thus, let
![]() $I\subseteq R$
be any
$I\subseteq R$
be any
![]() $\mathbb{Z}$
-graded ideal and assume for simplicity that
$\mathbb{Z}$
-graded ideal and assume for simplicity that
![]() $J$
is principally generated by an element of degree 1; for example,
$J$
is principally generated by an element of degree 1; for example,
![]() $J=(y)\subseteq S$
.
$J=(y)\subseteq S$
.
Lemma 3.10. Let
![]() $I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
$I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
![]() $J=(y)\subseteq S=\Bbbk [y]$
be
$J=(y)\subseteq S=\Bbbk [y]$
be
![]() $\mathbb{Z}$
-graded ideals, and set
$\mathbb{Z}$
-graded ideals, and set
![]() $T=R\otimes _{\Bbbk }S=\Bbbk [x_{1},\ldots ,x_{m},y]$
. For
$T=R\otimes _{\Bbbk }S=\Bbbk [x_{1},\ldots ,x_{m},y]$
. For
![]() $r\geqslant 2$
, the
$r\geqslant 2$
, the
![]() $r$
-linear strand
$r$
-linear strand
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
is the mapping cone of the chain map
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
is the mapping cone of the chain map
Proof. It is easy to see that a minimal
![]() $T$
-free resolution
$T$
-free resolution
![]() $L_{\bullet }(T/IT+JT)$
of
$L_{\bullet }(T/IT+JT)$
of
![]() $T/IT+JT$
is given by the mapping cone of the chain map
$T/IT+JT$
is given by the mapping cone of the chain map
![]() $\times y:L_{\bullet }(T/IT)(-1)\rightarrow L_{\bullet }(T/IT)$
, where
$\times y:L_{\bullet }(T/IT)(-1)\rightarrow L_{\bullet }(T/IT)$
, where
![]() $L_{\bullet }(T/IT)$
is a minimal
$L_{\bullet }(T/IT)$
is a minimal
![]() $T$
-free resolution of
$T$
-free resolution of
![]() $T/IT$
. Since the operation of taking the
$T/IT$
. Since the operation of taking the
![]() $r$
-linear strand commutes with the operation of taking the mapping cone, we are done.◻
$r$
-linear strand commutes with the operation of taking the mapping cone, we are done.◻
The general case is more involved. Assume now that
![]() $I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
$I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
![]() $J\subseteq S=\Bbbk [y_{1},\ldots ,y_{n}]$
are
$J\subseteq S=\Bbbk [y_{1},\ldots ,y_{n}]$
are
![]() $\mathbb{Z}$
-graded ideals such that
$\mathbb{Z}$
-graded ideals such that
![]() $I_{1}=0$
and
$I_{1}=0$
and
![]() $J_{1}=0$
. Let
$J_{1}=0$
. Let
![]() $L_{\bullet }(I)$
be a minimal graded
$L_{\bullet }(I)$
be a minimal graded
![]() $R$
-free resolution of
$R$
-free resolution of
![]() $I$
, and let
$I$
, and let
![]() $L_{\bullet }(J)$
be a minimal graded
$L_{\bullet }(J)$
be a minimal graded
![]() $S$
-free resolution of
$S$
-free resolution of
![]() $J$
, and consider their extensions
$J$
, and consider their extensions
![]() $L_{\bullet }(IT)$
and
$L_{\bullet }(IT)$
and
![]() $L_{\bullet }(JT)$
to
$L_{\bullet }(JT)$
to
![]() $T=R\otimes _{\Bbbk }S=\Bbbk [x_{1},\ldots ,x_{m},y_{1},\ldots ,y_{n}]$
.
$T=R\otimes _{\Bbbk }S=\Bbbk [x_{1},\ldots ,x_{m},y_{1},\ldots ,y_{n}]$
.
Lemma 3.11. Under the previous assumptions, the
![]() $r$
-linear strand
$r$
-linear strand
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
is
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
is
 $$\begin{eqnarray}\displaystyle \mathbb{L}_{\bullet }^{{<}r>}(IT+JT) & = & \displaystyle \mathbb{L}_{\bullet }^{{<}r>}(IT)\oplus \mathbb{L}_{\bullet }^{{<}r>}(JT)\nonumber\\ \displaystyle & \oplus & \displaystyle \left(\bigoplus _{a+b=r+1}(\mathbb{L}_{\bullet }^{{<}a>}(IT)\otimes _{T}\mathbb{L}_{\bullet }^{{<}b>}(JT))[-1]\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{L}_{\bullet }^{{<}r>}(IT+JT) & = & \displaystyle \mathbb{L}_{\bullet }^{{<}r>}(IT)\oplus \mathbb{L}_{\bullet }^{{<}r>}(JT)\nonumber\\ \displaystyle & \oplus & \displaystyle \left(\bigoplus _{a+b=r+1}(\mathbb{L}_{\bullet }^{{<}a>}(IT)\otimes _{T}\mathbb{L}_{\bullet }^{{<}b>}(JT))[-1]\right).\nonumber\end{eqnarray}$$
Here, for a chain complex
![]() $C_{\bullet }$
,
$C_{\bullet }$
,
![]() $C_{\bullet }[-1]$
denotes the translated complex whose component of homological degree
$C_{\bullet }[-1]$
denotes the translated complex whose component of homological degree
![]() $j$
is
$j$
is
![]() $C_{j-1}$
.
$C_{j-1}$
.
Proof. Consider the minimal
![]() $\mathbb{Z}$
-graded free resolutions of
$\mathbb{Z}$
-graded free resolutions of
![]() $R/I$
and
$R/I$
and
![]() $S/J$
, respectively,
$S/J$
, respectively,

where
![]() $L_{0}=R$
and
$L_{0}=R$
and
![]() ${L^{\prime }}_{0}=S$
. According to Proposition 3.8, the minimal
${L^{\prime }}_{0}=S$
. According to Proposition 3.8, the minimal
![]() $\mathbb{Z}$
-graded free resolution
$\mathbb{Z}$
-graded free resolution
![]() $L_{\bullet }(T/IT+JT)$
has the formFootnote
2
$L_{\bullet }(T/IT+JT)$
has the formFootnote
2

where, for any given
![]() $x_{i}\otimes y_{p-i}\in L_{i}\otimes L_{p-i}^{\prime }$
, we have
$x_{i}\otimes y_{p-i}\in L_{i}\otimes L_{p-i}^{\prime }$
, we have
To describe the
![]() $r$
-linear strand
$r$
-linear strand
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
of the ideal
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
of the ideal
![]() $IT+JT$
, we must consider the truncation at the first term of the above resolution and take a close look at the free modules and the components of the corresponding differentials. Recall that
$IT+JT$
, we must consider the truncation at the first term of the above resolution and take a close look at the free modules and the components of the corresponding differentials. Recall that
![]() $L_{\bullet }^{{<}r-1>}(R/I)$
corresponds to
$L_{\bullet }^{{<}r-1>}(R/I)$
corresponds to
![]() $L_{\bullet }^{{<}r>}(I)$
for all
$L_{\bullet }^{{<}r>}(I)$
for all
![]() $r\geqslant 2$
. It is easy to see that both
$r\geqslant 2$
. It is easy to see that both
and
are subcomplexes of
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
. Moreover,
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
. Moreover,
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT)$
and
$\mathbb{L}_{\bullet }^{{<}r>}(IT)$
and
![]() $\mathbb{L}_{\bullet }^{{<}r>}(JT)$
are direct summands of
$\mathbb{L}_{\bullet }^{{<}r>}(JT)$
are direct summands of
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
. In fact, since
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
. In fact, since
![]() $I_{1}=J_{1}=0$
, the linear parts of the maps
$I_{1}=J_{1}=0$
, the linear parts of the maps
![]() $L_{i}\otimes L_{1}^{\prime }\rightarrow L_{i}\otimes L_{0}^{\prime }$
and
$L_{i}\otimes L_{1}^{\prime }\rightarrow L_{i}\otimes L_{0}^{\prime }$
and
![]() $L_{1}\otimes L_{j}^{\prime }\rightarrow L_{0}\otimes L_{j}^{\prime }$
vanish.
$L_{1}\otimes L_{j}^{\prime }\rightarrow L_{0}\otimes L_{j}^{\prime }$
vanish.
In order to obtain the remaining components of
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
, we must consider the
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
, we must consider the
![]() $r$
-linear strand of
$r$
-linear strand of

This complex starts at the second term (i.e., the term of homological degree 1), and the first term of the
![]() $r$
-linear strand is
$r$
-linear strand is
![]() $\bigoplus _{a+b=r+1}\mathbb{L}_{0}^{{<}a>}(IT)\otimes _{T}\mathbb{L}_{0}^{{<}b>}(JT).$
If we take a close look at the free summands of these components and their differentials, we obtain the following description:
$\bigoplus _{a+b=r+1}\mathbb{L}_{0}^{{<}a>}(IT)\otimes _{T}\mathbb{L}_{0}^{{<}b>}(JT).$
If we take a close look at the free summands of these components and their differentials, we obtain the following description:
Therefore, we are done. ◻
The main result of this subsection is the following.
Proposition 3.12. The
![]() $\unicode[STIX]{x1D708}$
-numbers of
$\unicode[STIX]{x1D708}$
-numbers of
![]() $IT+JT$
have the following form.
$IT+JT$
have the following form.
(i) If
 $I_{1}\neq 0$
or
$I_{1}\neq 0$
or
 $J_{1}\neq 0$
, then
$J_{1}\neq 0$
, then
 $IT+JT$
has a trivial
$IT+JT$
has a trivial
 $\unicode[STIX]{x1D708}$
-table.
$\unicode[STIX]{x1D708}$
-table.(ii) If
 $I_{1}=0$
and
$I_{1}=0$
and
 $J_{1}=0$
, then we have
$J_{1}=0$
, then we have  $$\begin{eqnarray}\unicode[STIX]{x1D708}_{i,j}(IT+JT)=\unicode[STIX]{x1D708}_{i,j}(IT)+\unicode[STIX]{x1D708}_{i,j}(JT)+\mathop{\sum }_{\substack{ k+k^{\prime }=i-1 \\ l+l^{\prime }=j}}\unicode[STIX]{x1D708}_{k,l}(IT)\unicode[STIX]{x1D708}_{k^{\prime },l^{\prime }}(JT).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{i,j}(IT+JT)=\unicode[STIX]{x1D708}_{i,j}(IT)+\unicode[STIX]{x1D708}_{i,j}(JT)+\mathop{\sum }_{\substack{ k+k^{\prime }=i-1 \\ l+l^{\prime }=j}}\unicode[STIX]{x1D708}_{k,l}(IT)\unicode[STIX]{x1D708}_{k^{\prime },l^{\prime }}(JT).\end{eqnarray}$$
Proof. (i) If
![]() $J_{1}\neq 0$
, we may assume that
$J_{1}\neq 0$
, we may assume that
![]() $y_{n}\in J$
without loss of generality. Now, we have
$y_{n}\in J$
without loss of generality. Now, we have
![]() $J=(f_{1},\ldots ,f_{r},y_{n})$
, where
$J=(f_{1},\ldots ,f_{r},y_{n})$
, where
![]() $f_{1}\ldots ,f_{r}$
are homogeneous polynomials in
$f_{1}\ldots ,f_{r}$
are homogeneous polynomials in
![]() $\Bbbk [y_{1},\ldots .y_{n-1}]$
. Set
$\Bbbk [y_{1},\ldots .y_{n-1}]$
. Set
![]() $R^{\prime }:=\Bbbk [x_{1},\ldots ,x_{m},y_{1},\ldots ,y_{n-1}]$
,
$R^{\prime }:=\Bbbk [x_{1},\ldots ,x_{m},y_{1},\ldots ,y_{n-1}]$
,
![]() $S^{\prime }=\Bbbk [y_{n}]$
, and let
$S^{\prime }=\Bbbk [y_{n}]$
, and let
![]() $I^{\prime }=IR^{\prime }+(f_{1},\ldots ,f_{r})$
be an ideal in
$I^{\prime }=IR^{\prime }+(f_{1},\ldots ,f_{r})$
be an ideal in
![]() $R^{\prime }$
(note that
$R^{\prime }$
(note that
![]() $f_{1}\ldots ,f_{r}$
are elements in
$f_{1}\ldots ,f_{r}$
are elements in
![]() $R^{\prime }$
), and let
$R^{\prime }$
), and let
![]() $J^{\prime }=(y_{n})$
be an ideal in
$J^{\prime }=(y_{n})$
be an ideal in
![]() $S^{\prime }$
. Then, we have
$S^{\prime }$
. Then, we have
![]() $T=R\otimes _{\Bbbk }S=R^{\prime }\otimes _{\Bbbk }S^{\prime }$
, and
$T=R\otimes _{\Bbbk }S=R^{\prime }\otimes _{\Bbbk }S^{\prime }$
, and
![]() $IT+JT=I^{\prime }T+J^{\prime }T$
. This means that we may assume that
$IT+JT=I^{\prime }T+J^{\prime }T$
. This means that we may assume that
![]() $J=(y)\subseteq S=\Bbbk [y]$
from the beginning. For
$J=(y)\subseteq S=\Bbbk [y]$
from the beginning. For
![]() $r\geqslant 2$
, the
$r\geqslant 2$
, the
![]() $r$
-linear strand
$r$
-linear strand
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
is given by the mapping cone of the chain map
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)$
is given by the mapping cone of the chain map
![]() $\times y:(\mathbb{L}_{\bullet }^{{<}r>}(IT))(-1)\rightarrow \mathbb{L}_{\bullet }^{{<}r>}(IT)$
by Lemma 3.10. Hence,
$\times y:(\mathbb{L}_{\bullet }^{{<}r>}(IT))(-1)\rightarrow \mathbb{L}_{\bullet }^{{<}r>}(IT)$
by Lemma 3.10. Hence,
![]() $\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)\otimes _{T}\mathbb{K}$
is given by the mapping cone of the chain map
$\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)\otimes _{T}\mathbb{K}$
is given by the mapping cone of the chain map
where
![]() $\mathbb{K}$
is the field of fractions of
$\mathbb{K}$
is the field of fractions of
![]() $T$
. Clearly, this is the identity map, and its mapping cone is exact. This means that
$T$
. Clearly, this is the identity map, and its mapping cone is exact. This means that
![]() $H_{i}(\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)\otimes _{T}\mathbb{K})=0$
for all
$H_{i}(\mathbb{L}_{\bullet }^{{<}r>}(IT+JT)\otimes _{T}\mathbb{K})=0$
for all
![]() $r\geqslant 2$
and all
$r\geqslant 2$
and all
![]() $i$
.
$i$
.
On the other hand,
![]() $(IT+JT)_{{<}1>}$
is a complete intersection ideal generated by degree-1 elements, and hence we have
$(IT+JT)_{{<}1>}$
is a complete intersection ideal generated by degree-1 elements, and hence we have
![]() $\dim _{\mathbb{K}}H_{i}(\mathbb{L}_{\bullet }^{{<}1>}(I)\otimes _{T}\mathbb{K})=\unicode[STIX]{x1D6FF}_{0,i}$
. Summing up, we see that
$\dim _{\mathbb{K}}H_{i}(\mathbb{L}_{\bullet }^{{<}1>}(I)\otimes _{T}\mathbb{K})=\unicode[STIX]{x1D6FF}_{0,i}$
. Summing up, we see that
![]() $IT+JT$
has a trivial
$IT+JT$
has a trivial
![]() $\unicode[STIX]{x1D708}$
-table.
$\unicode[STIX]{x1D708}$
-table.
(ii) Follows immediately from Lemma 3.11. ◻
The following is just a rephrasing of part (i) of the previous result.
Corollary 3.13. Let
![]() $I\subseteq R$
be a
$I\subseteq R$
be a
![]() $\mathbb{Z}$
-graded ideal with
$\mathbb{Z}$
-graded ideal with
![]() $I_{1}\neq 0$
, then
$I_{1}\neq 0$
, then
![]() $I$
has a trivial
$I$
has a trivial
![]() $\unicode[STIX]{x1D708}$
-table.
$\unicode[STIX]{x1D708}$
-table.
The following is another corollary of Proposition 3.12.
Corollary 3.14. With the same notation as in Proposition 3.12, if
![]() $I_{1}=J_{1}=0$
, then
$I_{1}=J_{1}=0$
, then
![]() $IT+JT$
always has a nontrivial
$IT+JT$
always has a nontrivial
![]() $\unicode[STIX]{x1D708}$
-table.
$\unicode[STIX]{x1D708}$
-table.
Proof. Set
![]() $l:=\min \{i\mid I_{i}\neq 0\}$
and
$l:=\min \{i\mid I_{i}\neq 0\}$
and
![]() $l^{\prime }:=\min \{i\mid J_{i}\neq 0\}$
. Then, we have
$l^{\prime }:=\min \{i\mid J_{i}\neq 0\}$
. Then, we have
![]() $\unicode[STIX]{x1D708}_{1,l+l^{\prime }}(IT+JT)\geqslant \unicode[STIX]{x1D708}_{0,l}(IT)\unicode[STIX]{x1D708}_{0,l^{\prime }}(JT)>0$
by Proposition 3.12(ii).◻
$\unicode[STIX]{x1D708}_{1,l+l^{\prime }}(IT+JT)\geqslant \unicode[STIX]{x1D708}_{0,l}(IT)\unicode[STIX]{x1D708}_{0,l^{\prime }}(JT)>0$
by Proposition 3.12(ii).◻
4 Lyubeznik numbers versus
 $\unicode[STIX]{x1D708}$
-numbers for monomial ideals
$\unicode[STIX]{x1D708}$
-numbers for monomial ideals
In [Reference Yanagawa26], the second author showed that, via Alexander duality, the study of local cohomology modules with supports in monomial ideals can be translated into the study of the minimal free resolutions of squarefree monomial ideals. This fact was later refined by Vahidi and the first author in [Reference Àlvarez Montaner and Vahidi1] in order to study Lyubeznik numbers of squarefree monomial ideals in terms of the linear strands of their Alexander dual ideals. The aim of this section is to go further in this direction.
In the following, we only consider monomial ideals in the polynomial ring
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
, and
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
, and
![]() $\mathfrak{m}=(x_{1},\ldots ,x_{n})$
denotes the graded maximal ideal. Recall that Lyubeznik numbers are well defined in this nonlocal setting since they are invariant with respect to completion, so we consider
$\mathfrak{m}=(x_{1},\ldots ,x_{n})$
denotes the graded maximal ideal. Recall that Lyubeznik numbers are well defined in this nonlocal setting since they are invariant with respect to completion, so we consider
![]() $\unicode[STIX]{x1D706}_{p,i}(R/I)=\unicode[STIX]{x1D706}_{p,i}(\widehat{R}/I\widehat{R})$
, where
$\unicode[STIX]{x1D706}_{p,i}(R/I)=\unicode[STIX]{x1D706}_{p,i}(\widehat{R}/I\widehat{R})$
, where
![]() $\widehat{R}=\Bbbk [\![x_{1},\ldots ,x_{n}]\!]$
. For a vector
$\widehat{R}=\Bbbk [\![x_{1},\ldots ,x_{n}]\!]$
. For a vector
![]() $\mathbf{a}=(a_{1},\ldots ,a_{n})\in \mathbb{N}^{n}$
, set
$\mathbf{a}=(a_{1},\ldots ,a_{n})\in \mathbb{N}^{n}$
, set
![]() $\text{supp}(\mathbf{a}):=\{i\mid a_{i}\neq 0\}\subseteq \{1,\ldots ,n\}$
. For each
$\text{supp}(\mathbf{a}):=\{i\mid a_{i}\neq 0\}\subseteq \{1,\ldots ,n\}$
. For each
![]() $1\leqslant i\leqslant n$
, let
$1\leqslant i\leqslant n$
, let
![]() $\mathbf{e}_{i}\in \mathbb{Z}^{n}$
be the
$\mathbf{e}_{i}\in \mathbb{Z}^{n}$
be the
![]() $i$
th standard vector. The following notion was introduced by the second author, and serves as a powerful tool for combinatorial commutative algebra.
$i$
th standard vector. The following notion was introduced by the second author, and serves as a powerful tool for combinatorial commutative algebra.
Definition 4.1. We say that a finitely generated
![]() $\mathbb{N}^{n}$
-graded
$\mathbb{N}^{n}$
-graded
![]() $R$
-module
$R$
-module
![]() $M=\bigoplus _{\mathbf{a}\in \mathbb{N}^{n}}M_{\mathbf{a}}$
is squarefree if the multiplication map
$M=\bigoplus _{\mathbf{a}\in \mathbb{N}^{n}}M_{\mathbf{a}}$
is squarefree if the multiplication map
![]() $M_{\mathbf{a}}\ni y\longmapsto x_{i}y\in M_{\mathbf{a}+\mathbf{e}_{i}}$
is bijective for all
$M_{\mathbf{a}}\ni y\longmapsto x_{i}y\in M_{\mathbf{a}+\mathbf{e}_{i}}$
is bijective for all
![]() $\mathbf{a}\in \mathbb{N}^{n}$
and all
$\mathbf{a}\in \mathbb{N}^{n}$
and all
![]() $i\in \text{supp}(\mathbf{a})$
.
$i\in \text{supp}(\mathbf{a})$
.
The theory of squarefree modules is found in [Reference Yanagawa25, Reference Yanagawa26, Reference Yanagawa28, Reference Yanagawa29]. Here, we list some basic properties.
∙ For a monomial ideal
 $I$
, it is a squarefree
$I$
, it is a squarefree
 $R$
-module if and only if
$R$
-module if and only if
 $I=\sqrt{I}$
(equivalently, the Stanley–Reisner ideal
$I=\sqrt{I}$
(equivalently, the Stanley–Reisner ideal
 $I_{\unicode[STIX]{x1D6E5}}$
for some
$I_{\unicode[STIX]{x1D6E5}}$
for some
 $\unicode[STIX]{x1D6E5}$
). The free module
$\unicode[STIX]{x1D6E5}$
). The free module
 $R$
itself and the
$R$
itself and the
 $\mathbb{Z}^{n}$
-graded canonical module
$\mathbb{Z}^{n}$
-graded canonical module
 $\unicode[STIX]{x1D714}_{R}=R(-\mathbf{1})$
are squarefree. Here,
$\unicode[STIX]{x1D714}_{R}=R(-\mathbf{1})$
are squarefree. Here,
 $\mathbf{1}=(1,1,\ldots ,1)\in \mathbb{N}^{n}$
. The Stanley–Reisner ring
$\mathbf{1}=(1,1,\ldots ,1)\in \mathbb{N}^{n}$
. The Stanley–Reisner ring
 $R/I_{\unicode[STIX]{x1D6E5}}$
is also squarefree.
$R/I_{\unicode[STIX]{x1D6E5}}$
is also squarefree.∙ Let
 $M$
be a squarefree
$M$
be a squarefree
 $R$
-module, and let
$R$
-module, and let
 $L_{\bullet }$
be its
$L_{\bullet }$
be its
 $\mathbb{Z}^{n}$
-graded minimal free resolution. Then, the free module
$\mathbb{Z}^{n}$
-graded minimal free resolution. Then, the free module
 $L_{i}$
and the syzygy module
$L_{i}$
and the syzygy module
 $\operatorname{Syz}_{i}(M)$
are squarefree for each
$\operatorname{Syz}_{i}(M)$
are squarefree for each
 $i$
. Moreover,
$i$
. Moreover,
 $\text{Ext}_{R}^{i}(M,\unicode[STIX]{x1D714}_{R})$
is squarefree for all
$\text{Ext}_{R}^{i}(M,\unicode[STIX]{x1D714}_{R})$
is squarefree for all
 $i$
.
$i$
.∙ Let
 $\operatorname{ \ast mod}R$
be the category of
$\operatorname{ \ast mod}R$
be the category of
 $\mathbb{Z}^{n}$
-graded finitely generated
$\mathbb{Z}^{n}$
-graded finitely generated
 $R$
-modules, and let
$R$
-modules, and let
 $\operatorname{Sq}R$
be its full subcategory consisting of squarefree modules. Then,
$\operatorname{Sq}R$
be its full subcategory consisting of squarefree modules. Then,
 $\operatorname{Sq}R$
is an abelian subcategory of
$\operatorname{Sq}R$
is an abelian subcategory of
 $\operatorname{ \ast mod}R$
. We have an exact contravariant functor
$\operatorname{ \ast mod}R$
. We have an exact contravariant functor
 $\mathbf{A}$
from
$\mathbf{A}$
from
 $\operatorname{Sq}R$
to itself. The construction of
$\operatorname{Sq}R$
to itself. The construction of
 $\mathbf{A}$
is found in (for example) [Reference Yanagawa29]. Here, we just remark that
$\mathbf{A}$
is found in (for example) [Reference Yanagawa29]. Here, we just remark that
 $\mathbf{A}(R/I_{\unicode[STIX]{x1D6E5}})\cong I_{\unicode[STIX]{x1D6E5}^{\vee }}$
, where
$\mathbf{A}(R/I_{\unicode[STIX]{x1D6E5}})\cong I_{\unicode[STIX]{x1D6E5}^{\vee }}$
, where
 $\unicode[STIX]{x1D6E5}^{\vee }:=\{F\subseteq \{1,\ldots ,n\}\mid (\{1,\ldots ,n\}\setminus F)\not \in \unicode[STIX]{x1D6E5}\}$
is the Alexander dual simplicial complex of
$\unicode[STIX]{x1D6E5}^{\vee }:=\{F\subseteq \{1,\ldots ,n\}\mid (\{1,\ldots ,n\}\setminus F)\not \in \unicode[STIX]{x1D6E5}\}$
is the Alexander dual simplicial complex of
 $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
In this framework, we have the following description of Lyubeznik numbers.
Theorem 4.2. [Reference Yanagawa26, Corollary 3.10]
Let
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
be a polynomial ring, and let
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
be a polynomial ring, and let
![]() $I_{\unicode[STIX]{x1D6E5}}$
be a squarefree monomial ideal. Then, we have
$I_{\unicode[STIX]{x1D6E5}}$
be a squarefree monomial ideal. Then, we have
For a squarefree
![]() $R$
-module
$R$
-module
![]() $M$
, the second author defined the cochain complex
$M$
, the second author defined the cochain complex
![]() $\mathbf{D}\,(M)$
of squarefree
$\mathbf{D}\,(M)$
of squarefree
![]() $R$
-modules satisfying
$R$
-modules satisfying
![]() $H^{i}(\mathbf{D}\,(M))\cong \text{Ext}_{R}^{n+i}(M,\unicode[STIX]{x1D714}_{R})$
for all
$H^{i}(\mathbf{D}\,(M))\cong \text{Ext}_{R}^{n+i}(M,\unicode[STIX]{x1D714}_{R})$
for all
![]() $i$
(see [Reference Yanagawa29, Section 3]). By [Reference Yanagawa25, Theorem 4.1] or [Reference Yanagawa28, Theorem 3.8], we have the isomorphism
$i$
(see [Reference Yanagawa29, Section 3]). By [Reference Yanagawa25, Theorem 4.1] or [Reference Yanagawa28, Theorem 3.8], we have the isomorphism
of cochain complexes of
![]() $\mathbb{Z}^{n}$
-graded
$\mathbb{Z}^{n}$
-graded
![]() $R$
-modulesFootnote
3
. Here, for a cochain complex
$R$
-modulesFootnote
3
. Here, for a cochain complex
![]() $C^{\bullet }$
,
$C^{\bullet }$
,
![]() $C^{\bullet }[-i]$
means the
$C^{\bullet }[-i]$
means the
![]() $-i$
th translation of
$-i$
th translation of
![]() $C^{\bullet }$
. More precisely, it is the cochain complex whose component of cohomological degree
$C^{\bullet }$
. More precisely, it is the cochain complex whose component of cohomological degree
![]() $j$
is
$j$
is
![]() $C^{j-i}$
, and we regard a chain complex
$C^{j-i}$
, and we regard a chain complex
![]() $C_{\bullet }$
as the cochain complex whose component of cohomological degree
$C_{\bullet }$
as the cochain complex whose component of cohomological degree
![]() $j$
is
$j$
is
![]() $C_{-j}$
.
$C_{-j}$
.
The following is a variant of a result given by the first author and Vahidi.
Theorem 4.3. (Cf. [Reference Àlvarez Montaner and Vahidi1, Corollary 4.2])
Let
![]() $I_{\unicode[STIX]{x1D6E5}}\subseteq R=\Bbbk [x_{1},\ldots ,x_{n}]$
be a squarefree monomial ideal. Then, we have
$I_{\unicode[STIX]{x1D6E5}}\subseteq R=\Bbbk [x_{1},\ldots ,x_{n}]$
be a squarefree monomial ideal. Then, we have
Proof. By (4.1) and the construction of
![]() $\mathbf{A}$
, we have an isomorphism
$\mathbf{A}$
, we have an isomorphism
of cochain complexes of
![]() $\Bbbk$
-vector spaces. Here,
$\Bbbk$
-vector spaces. Here,
![]() $(-)^{\ast }$
means the
$(-)^{\ast }$
means the
![]() $\Bbbk$
-dual. We also remark that, for a squarefree module
$\Bbbk$
-dual. We also remark that, for a squarefree module
![]() $M$
, we have
$M$
, we have
Thus, we have the following computation:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{p,i}(R/I_{\unicode[STIX]{x1D6E5}}) & = & \displaystyle \dim _{\Bbbk }[\text{Ext}_{R}^{n-p}(\text{Ext}_{R}^{n-i}(R/I,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\nonumber\\ \displaystyle & = & \displaystyle \dim _{\Bbbk }[H^{-p}(\mathbf{D}\,(\text{Ext}_{R}^{n-i}(R/I,\unicode[STIX]{x1D714}_{R})))]_{0}\nonumber\\ \displaystyle & = & \displaystyle \dim _{\Bbbk }[H_{i-p}(\mathbb{L}_{\bullet }^{{<}n-i>}(I_{\unicode[STIX]{x1D6E5}^{\vee }}))]_{\mathbf{1}}\nonumber\\ \displaystyle & = & \displaystyle \dim _{\mathbb{K}}H_{i-p}(\mathbb{L}_{\bullet }^{{<}n-i>}(I_{\unicode[STIX]{x1D6E5}^{\vee }}))\otimes _{R}\mathbb{K}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D708}_{i-p,n-p}(I_{\unicode[STIX]{x1D6E5}^{\vee }}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{p,i}(R/I_{\unicode[STIX]{x1D6E5}}) & = & \displaystyle \dim _{\Bbbk }[\text{Ext}_{R}^{n-p}(\text{Ext}_{R}^{n-i}(R/I,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\nonumber\\ \displaystyle & = & \displaystyle \dim _{\Bbbk }[H^{-p}(\mathbf{D}\,(\text{Ext}_{R}^{n-i}(R/I,\unicode[STIX]{x1D714}_{R})))]_{0}\nonumber\\ \displaystyle & = & \displaystyle \dim _{\Bbbk }[H_{i-p}(\mathbb{L}_{\bullet }^{{<}n-i>}(I_{\unicode[STIX]{x1D6E5}^{\vee }}))]_{\mathbf{1}}\nonumber\\ \displaystyle & = & \displaystyle \dim _{\mathbb{K}}H_{i-p}(\mathbb{L}_{\bullet }^{{<}n-i>}(I_{\unicode[STIX]{x1D6E5}^{\vee }}))\otimes _{R}\mathbb{K}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D708}_{i-p,n-p}(I_{\unicode[STIX]{x1D6E5}^{\vee }}).\nonumber\end{eqnarray}$$
As mentioned in the introduction, for a local ring
![]() $A$
containing a field, we have
$A$
containing a field, we have
In the monomial ideal case, this equation is an immediate consequence of Lemma 3.2 and Theorem 4.3.
As a special case of Theorem 2.1, the Lyubeznik tables of monomial ideals in
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
satisfy the consecutiveness property of nontrivial superdiagonals. However, this also follows from the consecutiveness property of nontrivial columns of the
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
satisfy the consecutiveness property of nontrivial superdiagonals. However, this also follows from the consecutiveness property of nontrivial columns of the
![]() $\unicode[STIX]{x1D708}$
-tables (Theorem 3.7) via Theorem 4.3. In this sense, both “consecutiveness theorems” are related.
$\unicode[STIX]{x1D708}$
-tables (Theorem 3.7) via Theorem 4.3. In this sense, both “consecutiveness theorems” are related.
4.1 Sequentially Cohen–Macaulay rings
Let
![]() $M$
be a finitely generated graded module over the polynomial ring
$M$
be a finitely generated graded module over the polynomial ring
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
. We say that
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
. We say that
![]() $M$
is sequentially Cohen–Macaulay if
$M$
is sequentially Cohen–Macaulay if
![]() $\text{Ext}_{R}^{n-i}(M,R)$
is either a Cohen–Macaulay module of dimension
$\text{Ext}_{R}^{n-i}(M,R)$
is either a Cohen–Macaulay module of dimension
![]() $i$
or the 0 module for all
$i$
or the 0 module for all
![]() $i$
. The original definition is given by the existence of a certain filtration (see [Reference Stanley22, III, Definition 2.9]). However, it is equivalent to the above one by [Reference Stanley22, III, Theorem 2.11]. The sequentially Cohen–Macaulay property of a finitely generated module over a regular local ring is defined/characterized in the same way.
$i$
. The original definition is given by the existence of a certain filtration (see [Reference Stanley22, III, Definition 2.9]). However, it is equivalent to the above one by [Reference Stanley22, III, Theorem 2.11]. The sequentially Cohen–Macaulay property of a finitely generated module over a regular local ring is defined/characterized in the same way.
In [Reference Àlvarez Montaner2], the first author showed that the sequentially Cohen–Macaulay property implies the triviality of Lyubeznik tables in positive characteristic as well as in the case of squarefree monomial ideals. Using Proposition 3.6, we can give a new proof/interpretation of this result for the case of monomial ideals.
Proposition 4.4. (Cf. [Reference Àlvarez Montaner2, Theorem 3.2])
Let
![]() $I$
be a monomial ideal of the polynomial ring
$I$
be a monomial ideal of the polynomial ring
![]() $R=\Bbbk [x_{1},\ldots ,x_{n}]$
such that
$R=\Bbbk [x_{1},\ldots ,x_{n}]$
such that
![]() $R/I$
is sequentially Cohen–Macaulay. Then, the Lyubeznik table of
$R/I$
is sequentially Cohen–Macaulay. Then, the Lyubeznik table of
![]() $R/I$
is trivial.
$R/I$
is trivial.
Proof. By [Reference Herzog, Takayama and Terai9, Theorem 2.6],
![]() $R/\sqrt{I}$
is sequentially Cohen–Macaulay again. Hence, we may assume that
$R/\sqrt{I}$
is sequentially Cohen–Macaulay again. Hence, we may assume that
![]() $I$
is the Stanley–Reisner ideal
$I$
is the Stanley–Reisner ideal
![]() $I_{\unicode[STIX]{x1D6E5}}$
of a simplicial complex
$I_{\unicode[STIX]{x1D6E5}}$
of a simplicial complex
![]() $\unicode[STIX]{x1D6E5}$
. Herzog and Hibi [Reference Herzog and Hibi8] showed that
$\unicode[STIX]{x1D6E5}$
. Herzog and Hibi [Reference Herzog and Hibi8] showed that
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
is sequentially Cohen–Macaulay if and only if
$R/I_{\unicode[STIX]{x1D6E5}}$
is sequentially Cohen–Macaulay if and only if
![]() $I_{\unicode[STIX]{x1D6E5}^{\vee }}$
is componentwise linear. Now, the assertion immediately follows from Proposition 3.6 and Theorem 4.3.◻
$I_{\unicode[STIX]{x1D6E5}^{\vee }}$
is componentwise linear. Now, the assertion immediately follows from Proposition 3.6 and Theorem 4.3.◻
The converse of Proposition 4.4 is not true. That is, even if
![]() $R/I$
has a trivial Lyubeznik table, it need not be sequentially Cohen–Macaulay. For example, if
$R/I$
has a trivial Lyubeznik table, it need not be sequentially Cohen–Macaulay. For example, if
![]() $I$
is the monomial ideal
$I$
is the monomial ideal
in
![]() $R=\Bbbk [x_{1},\ldots ,x_{5}]$
, then
$R=\Bbbk [x_{1},\ldots ,x_{5}]$
, then
![]() $R/I$
has a trivial Lyubeznik table, but this ring is not sequentially Cohen–Macaulay. Since all associated primes of
$R/I$
has a trivial Lyubeznik table, but this ring is not sequentially Cohen–Macaulay. Since all associated primes of
![]() $I$
have the same height, it is the same to say that
$I$
have the same height, it is the same to say that
![]() $R/I$
is not Cohen–Macaulay. However,
$R/I$
is not Cohen–Macaulay. However,
![]() $R/I$
does not even satisfy Serre’s condition
$R/I$
does not even satisfy Serre’s condition
![]() $(S_{2})$
.
$(S_{2})$
.
In Proposition 4.5 below, we see that if a monomial ideal
![]() $I$
has height 1 (i.e., admits a height one associated prime), then the Lyubeznik table of
$I$
has height 1 (i.e., admits a height one associated prime), then the Lyubeznik table of
![]() $R/I$
is trivial. Of course,
$R/I$
is trivial. Of course,
![]() $R/I$
need not be sequentially Cohen–Macaulay in this situation.
$R/I$
need not be sequentially Cohen–Macaulay in this situation.
4.2 Thom–Sebastiani type formulas
Let
![]() $I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
$I\subseteq R=\Bbbk [x_{1},\ldots ,x_{m}]$
and
![]() $J\subseteq S=\Bbbk [y_{1},\ldots ,y_{n}]$
be squarefree monomial ideals in two disjoint sets of variables. Let
$J\subseteq S=\Bbbk [y_{1},\ldots ,y_{n}]$
be squarefree monomial ideals in two disjoint sets of variables. Let
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
be the simplicial complexes associated to
$\unicode[STIX]{x1D6E5}_{2}$
be the simplicial complexes associated to
![]() $I$
and
$I$
and
![]() $J$
by the Stanley–Reisner correspondence; that is,
$J$
by the Stanley–Reisner correspondence; that is,
![]() $I=I_{\unicode[STIX]{x1D6E5}_{1}}$
and
$I=I_{\unicode[STIX]{x1D6E5}_{1}}$
and
![]() $J=I_{\unicode[STIX]{x1D6E5}_{2}}$
. Then, the sum
$J=I_{\unicode[STIX]{x1D6E5}_{2}}$
. Then, the sum
![]() $IT+JT=I_{\unicode[STIX]{x1D6E5}_{1}\ast \unicode[STIX]{x1D6E5}_{2}}$
corresponds to the simplicial join of the two complexes. Let
$IT+JT=I_{\unicode[STIX]{x1D6E5}_{1}\ast \unicode[STIX]{x1D6E5}_{2}}$
corresponds to the simplicial join of the two complexes. Let
![]() $\unicode[STIX]{x1D6E5}_{1}^{\vee }$
(resp.
$\unicode[STIX]{x1D6E5}_{1}^{\vee }$
(resp.
![]() $\unicode[STIX]{x1D6E5}_{2}^{\vee }$
) be the Alexander dual of
$\unicode[STIX]{x1D6E5}_{2}^{\vee }$
) be the Alexander dual of
![]() $\unicode[STIX]{x1D6E5}_{1}$
(resp.
$\unicode[STIX]{x1D6E5}_{1}$
(resp.
![]() $\unicode[STIX]{x1D6E5}_{2}$
) as a simplicial complex on
$\unicode[STIX]{x1D6E5}_{2}$
) as a simplicial complex on
![]() $\{1,2,\ldots ,m\}$
(resp.
$\{1,2,\ldots ,m\}$
(resp.
![]() $\{1,2,\ldots ,n\}$
). Set
$\{1,2,\ldots ,n\}$
). Set
![]() $I^{\vee }:=I_{\unicode[STIX]{x1D6E5}_{1}^{\vee }}\subseteq R$
and
$I^{\vee }:=I_{\unicode[STIX]{x1D6E5}_{1}^{\vee }}\subseteq R$
and
![]() $J^{\vee }:=I_{\unicode[STIX]{x1D6E5}_{2}^{\vee }}\subseteq S$
. Then, it is easy to see that
$J^{\vee }:=I_{\unicode[STIX]{x1D6E5}_{2}^{\vee }}\subseteq S$
. Then, it is easy to see that
where
![]() $\mathbf{A}$
denotes the Alexander duality functor of
$\mathbf{A}$
denotes the Alexander duality functor of
![]() $\operatorname{Sq}T$
.
$\operatorname{Sq}T$
.
Proposition 4.5. The Lyubeznik numbers of
![]() $T/IT\cap JT$
have the following form.
$T/IT\cap JT$
have the following form.
(i) If either the height of
 $I$
or the height of
$I$
or the height of
 $J$
is
$J$
is
 $1$
, then
$1$
, then
 $T/IT\cap JT$
has a trivial Lyubeznik table.
$T/IT\cap JT$
has a trivial Lyubeznik table.(ii) If both the height of
 $I$
and the height of
$I$
and the height of
 $J$
are
$J$
are
 ${\geqslant}2$
, then we have
${\geqslant}2$
, then we have  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{p,i}(T/IT\cap JT) & = & \displaystyle \unicode[STIX]{x1D706}_{p,i}(T/IT)+\unicode[STIX]{x1D706}_{p,i}(T/JT)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\substack{ q+r=p+\dim T \\ j+k=i+\dim T-1}}\unicode[STIX]{x1D706}_{q,j}(T/IT)\unicode[STIX]{x1D706}_{r,k}(T/JT)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}_{p-n,i-n}(R/I)+\unicode[STIX]{x1D706}_{p-m,i-m}(S/J)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\substack{ q+r=p \\ j+k=i-1}}\unicode[STIX]{x1D706}_{q,j}(R/I)\unicode[STIX]{x1D706}_{r,k}(S/J).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{p,i}(T/IT\cap JT) & = & \displaystyle \unicode[STIX]{x1D706}_{p,i}(T/IT)+\unicode[STIX]{x1D706}_{p,i}(T/JT)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\substack{ q+r=p+\dim T \\ j+k=i+\dim T-1}}\unicode[STIX]{x1D706}_{q,j}(T/IT)\unicode[STIX]{x1D706}_{r,k}(T/JT)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}_{p-n,i-n}(R/I)+\unicode[STIX]{x1D706}_{p-m,i-m}(S/J)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\substack{ q+r=p \\ j+k=i-1}}\unicode[STIX]{x1D706}_{q,j}(R/I)\unicode[STIX]{x1D706}_{r,k}(S/J).\nonumber\end{eqnarray}$$
Proof. The assertion easily follows from Proposition 3.12 and Theorem 4.3, but for completeness we will make a few remarks.
(i) Recall that, for a simplicial complex
![]() $\unicode[STIX]{x1D6E5}$
, the height of
$\unicode[STIX]{x1D6E5}$
, the height of
![]() $I_{\unicode[STIX]{x1D6E5}}$
is 1 if and only if
$I_{\unicode[STIX]{x1D6E5}}$
is 1 if and only if
![]() $[I_{\unicode[STIX]{x1D6E5}^{\vee }}]_{1}\neq 0$
.
$[I_{\unicode[STIX]{x1D6E5}^{\vee }}]_{1}\neq 0$
.
(ii) The last equality follows from the fact that
which can be seen from Theorem 4.3 and the construction of linear strands. ◻
Example 4.6. It is well known that local cohomology modules as well as free resolutions depend on the characteristic of the base field, so Lyubeznik numbers depend on the characteristic as well. The most recurrent example is the Stanley–Reisner ideal associated to a minimal triangulation of
![]() $\mathbb{P}_{\mathbb{R}}^{2}$
; that is, the ideal in
$\mathbb{P}_{\mathbb{R}}^{2}$
; that is, the ideal in
![]() $R=\Bbbk [x_{1},\ldots ,x_{6}]$
:
$R=\Bbbk [x_{1},\ldots ,x_{6}]$
:
Its Lyubeznik table has been computed in [Reference Àlvarez Montaner and Vahidi1, Example 4.8]. Namely, in characteristic zero and two respectively, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}(R/I)=\left(\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ & 0 & 0 & 0\\ & & 0 & 0\\ & & & 1\end{array}\right),\qquad \unicode[STIX]{x1D6EC}_{\mathbb{Z}/2\mathbb{Z}}(R/I)=\left(\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ & 0 & 0 & 0\\ & & 0 & 1\\ & & & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}(R/I)=\left(\begin{array}{@{}cccc@{}}0 & 0 & 0 & 0\\ & 0 & 0 & 0\\ & & 0 & 0\\ & & & 1\end{array}\right),\qquad \unicode[STIX]{x1D6EC}_{\mathbb{Z}/2\mathbb{Z}}(R/I)=\left(\begin{array}{@{}cccc@{}}0 & 0 & 1 & 0\\ & 0 & 0 & 0\\ & & 0 & 1\\ & & & 1\end{array}\right).\end{eqnarray}$$
One can slightly modify this example and use Proposition 4.5 to obtain some interesting behavior of Lyubeznik numbers.
![]() $\bullet$
The ideal
$\bullet$
The ideal
![]() $J=I\cap (x_{7})$
in
$J=I\cap (x_{7})$
in
![]() $R=\Bbbk [x_{1},\ldots ,x_{7}]$
has a trivial Lyubeznik table in any characteristic, so we obtain an example where the local cohomology modules depend on the characteristic but Lyubeznik numbers do not.
$R=\Bbbk [x_{1},\ldots ,x_{7}]$
has a trivial Lyubeznik table in any characteristic, so we obtain an example where the local cohomology modules depend on the characteristic but Lyubeznik numbers do not.
![]() $\bullet$
The ideal
$\bullet$
The ideal
![]() $J=I\cap (x_{7},x_{8})\cap (x_{9},x_{10})$
in
$J=I\cap (x_{7},x_{8})\cap (x_{9},x_{10})$
in
![]() $R=\Bbbk [x_{1},\ldots ,x_{10}]$
satisfies
$R=\Bbbk [x_{1},\ldots ,x_{10}]$
satisfies
and both Lyubeznik numbers are different from zero.
5 Lyubeznik table is a topological invariant
While the other sections treat the case where
![]() $R$
is a regular local ring or a polynomial ring, in this section we work in a slightly different situation. Here, the ring
$R$
is a regular local ring or a polynomial ring, in this section we work in a slightly different situation. Here, the ring
![]() $R$
means a normal semigroup ring. When
$R$
means a normal semigroup ring. When
![]() $R$
is simplicial and Gorenstein, the second author proved in [Reference Yanagawa27] that the local cohomology modules
$R$
is simplicial and Gorenstein, the second author proved in [Reference Yanagawa27] that the local cohomology modules
![]() $H_{I}^{r}(R)$
have finite Bass numbers for radical monomial ideals
$H_{I}^{r}(R)$
have finite Bass numbers for radical monomial ideals
![]() $I\subset R$
. In fact, without these conditions, Bass numbers are out of control and can be infinite (see [Reference Helm and Miller7] for details).
$I\subset R$
. In fact, without these conditions, Bass numbers are out of control and can be infinite (see [Reference Helm and Miller7] for details).
Before going to the main result of this section (Theorem 5.3), we introduce the setup that we work with. For more details, we refer to [Reference Yanagawa27].
Let
![]() $C\subset \mathbb{Z}^{n}$
be an affine semigroup (i.e.,
$C\subset \mathbb{Z}^{n}$
be an affine semigroup (i.e.,
![]() $C$
is a finitely generated additive submonoid of
$C$
is a finitely generated additive submonoid of
![]() $\mathbb{Z}^{n}$
), and let
$\mathbb{Z}^{n}$
), and let
![]() $R:=\Bbbk [\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C]\subset \Bbbk [x_{1}^{\pm 1},\ldots ,x_{n}^{\pm 1}]$
be the semigroup ring of
$R:=\Bbbk [\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C]\subset \Bbbk [x_{1}^{\pm 1},\ldots ,x_{n}^{\pm 1}]$
be the semigroup ring of
![]() $C$
over
$C$
over
![]() $\Bbbk$
. Here,
$\Bbbk$
. Here,
![]() $\mathbf{x}^{\mathbf{c}\,}$
denotes the monomial
$\mathbf{x}^{\mathbf{c}\,}$
denotes the monomial
![]() $\prod _{i=1}^{n}x_{i}^{c_{i}}$
for
$\prod _{i=1}^{n}x_{i}^{c_{i}}$
for
![]() $\mathbf{c}\,=(c_{1},\ldots ,c_{n})\in C$
. Regarding
$\mathbf{c}\,=(c_{1},\ldots ,c_{n})\in C$
. Regarding
![]() $C$
as a subset of
$C$
as a subset of
![]() $\mathbb{R}^{n}=\mathbb{R}\otimes _{\mathbb{Z}}\mathbb{Z}^{n}$
, let
$\mathbb{R}^{n}=\mathbb{R}\otimes _{\mathbb{Z}}\mathbb{Z}^{n}$
, let
![]() $P:=\mathbb{R}_{{\geqslant}0}C\subset \mathbb{R}^{n}$
be the polyhedral cone spanned by
$P:=\mathbb{R}_{{\geqslant}0}C\subset \mathbb{R}^{n}$
be the polyhedral cone spanned by
![]() $C$
. We always assume that
$C$
. We always assume that
![]() $\mathbb{Z}C=\mathbb{Z}^{n}$
,
$\mathbb{Z}C=\mathbb{Z}^{n}$
,
![]() $\mathbb{Z}^{n}\cap P=C$
and
$\mathbb{Z}^{n}\cap P=C$
and
![]() $C\cap (-C)=\{0\}$
. Thus,
$C\cap (-C)=\{0\}$
. Thus,
![]() $R$
is a normal Cohen–Macaulay integral domain of dimension
$R$
is a normal Cohen–Macaulay integral domain of dimension
![]() $n$
with the graded maximal ideal
$n$
with the graded maximal ideal
![]() $\mathfrak{m}:=(\mathbf{x}^{\mathbf{c}\,}\mid 0\neq \mathbf{c}\,\in C)$
. We say that
$\mathfrak{m}:=(\mathbf{x}^{\mathbf{c}\,}\mid 0\neq \mathbf{c}\,\in C)$
. We say that
![]() $R$
is simplicial if the cone
$R$
is simplicial if the cone
![]() $P$
is spanned by
$P$
is spanned by
![]() $n$
vectors in
$n$
vectors in
![]() $\mathbb{R}^{n}$
. The polynomial ring
$\mathbb{R}^{n}$
. The polynomial ring
![]() $\Bbbk [x_{1},\ldots ,x_{n}]$
is a typical example of a simplicial semigroup ring
$\Bbbk [x_{1},\ldots ,x_{n}]$
is a typical example of a simplicial semigroup ring
![]() $\Bbbk [C]$
for
$\Bbbk [C]$
for
![]() $C=\mathbb{N}^{n}$
. Clearly,
$C=\mathbb{N}^{n}$
. Clearly,
![]() $R=\bigoplus _{\mathbf{c}\,\in C}\Bbbk \,\mathbf{x}^{\mathbf{c}\,}$
is a
$R=\bigoplus _{\mathbf{c}\,\in C}\Bbbk \,\mathbf{x}^{\mathbf{c}\,}$
is a
![]() $\mathbb{Z}^{n}$
-graded ring. We say that a
$\mathbb{Z}^{n}$
-graded ring. We say that a
![]() $\mathbb{Z}^{n}$
-graded ideal of
$\mathbb{Z}^{n}$
-graded ideal of
![]() $R$
is a monomial ideal, and we denote by
$R$
is a monomial ideal, and we denote by
![]() $\operatorname{ \ast mod}R$
the category of finitely generated
$\operatorname{ \ast mod}R$
the category of finitely generated
![]() $\mathbb{Z}^{n}$
-graded
$\mathbb{Z}^{n}$
-graded
![]() $R$
-modules and degree preserving
$R$
-modules and degree preserving
![]() $R$
-homomorphisms.
$R$
-homomorphisms.
Let
![]() $L$
be the set of nonempty faces of the polyhedral cone
$L$
be the set of nonempty faces of the polyhedral cone
![]() $P$
. Note that
$P$
. Note that
![]() $\{0\}$
and
$\{0\}$
and
![]() $P$
itself belong to
$P$
itself belong to
![]() $L$
. Regarding
$L$
. Regarding
![]() $L$
as a partially ordered set by inclusion,
$L$
as a partially ordered set by inclusion,
![]() $R$
is simplicial if and only if
$R$
is simplicial if and only if
![]() $L$
is isomorphic to the power set
$L$
is isomorphic to the power set
![]() $2^{\{1,\ldots ,n\}}$
. For
$2^{\{1,\ldots ,n\}}$
. For
![]() $F\in L$
,
$F\in L$
,
![]() $\mathfrak{p}_{F}:=(\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C\setminus F)$
is a prime ideal of
$\mathfrak{p}_{F}:=(\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C\setminus F)$
is a prime ideal of
![]() $R$
. Conversely, any monomial prime ideal is of the form
$R$
. Conversely, any monomial prime ideal is of the form
![]() $\mathfrak{p}_{F}$
for some
$\mathfrak{p}_{F}$
for some
![]() $F\in L$
. Note that
$F\in L$
. Note that
![]() $R/\mathfrak{p}_{F}\cong \Bbbk [\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C\cap F]$
for
$R/\mathfrak{p}_{F}\cong \Bbbk [\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C\cap F]$
for
![]() $F\in L$
. For a point
$F\in L$
. For a point
![]() $\mathbf{c}\,\in C$
, we always have a unique face
$\mathbf{c}\,\in C$
, we always have a unique face
![]() $F\in L$
whose relative interior contains
$F\in L$
whose relative interior contains
![]() $\mathbf{c}\,$
. Here, we denote
$\mathbf{c}\,$
. Here, we denote
![]() $s(\mathbf{c}\,)=F$
.
$s(\mathbf{c}\,)=F$
.
The following is a generalization of the notion of squarefree modules (see Definition 4.1) to this setting.
Definition 5.1. [Reference Yanagawa27]
We say that a module
![]() $M\in \operatorname{\ast mod}R$
is squarefree if it is
$M\in \operatorname{\ast mod}R$
is squarefree if it is
![]() $C$
-graded (i.e.,
$C$
-graded (i.e.,
![]() $M_{\mathbf{a}}=0$
for all
$M_{\mathbf{a}}=0$
for all
![]() $\mathbf{a}\not \in C$
), and the multiplication map
$\mathbf{a}\not \in C$
), and the multiplication map
![]() $M_{\mathbf{a}}\ni y\longmapsto \mathbf{x}^{\mathbf{b}}y\in M_{\mathbf{a}+\mathbf{b}}$
is bijective for all
$M_{\mathbf{a}}\ni y\longmapsto \mathbf{x}^{\mathbf{b}}y\in M_{\mathbf{a}+\mathbf{b}}$
is bijective for all
![]() $\mathbf{a},\mathbf{b}\in C$
with
$\mathbf{a},\mathbf{b}\in C$
with
![]() $s(\mathbf{a}+\mathbf{b})=s(\mathbf{a})$
.
$s(\mathbf{a}+\mathbf{b})=s(\mathbf{a})$
.
For a monomial ideal
![]() $I$
,
$I$
,
![]() $R/I$
is a squarefree
$R/I$
is a squarefree
![]() $R$
-module if and only if
$R$
-module if and only if
![]() $I$
is a radical ideal (i.e.,
$I$
is a radical ideal (i.e.,
![]() $\sqrt{I}=I$
). We say that
$\sqrt{I}=I$
). We say that
![]() $\unicode[STIX]{x1D6E5}\subseteq L$
is an order ideal if
$\unicode[STIX]{x1D6E5}\subseteq L$
is an order ideal if
![]() $\unicode[STIX]{x1D6E5}\ni F\supset F^{\prime }\in L$
implies
$\unicode[STIX]{x1D6E5}\ni F\supset F^{\prime }\in L$
implies
![]() $F^{\prime }\in \unicode[STIX]{x1D6E5}$
. If
$F^{\prime }\in \unicode[STIX]{x1D6E5}$
. If
![]() $\unicode[STIX]{x1D6E5}$
is an order ideal, then
$\unicode[STIX]{x1D6E5}$
is an order ideal, then
![]() $I_{\unicode[STIX]{x1D6E5}}:=(\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C,\,s(\mathbf{c}\,)\not \in \unicode[STIX]{x1D6E5})\subseteq R$
is a radical monomial ideal. Conversely, any radical monomial ideal is of the form
$I_{\unicode[STIX]{x1D6E5}}:=(\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C,\,s(\mathbf{c}\,)\not \in \unicode[STIX]{x1D6E5})\subseteq R$
is a radical monomial ideal. Conversely, any radical monomial ideal is of the form
![]() $I_{\unicode[STIX]{x1D6E5}}$
for some
$I_{\unicode[STIX]{x1D6E5}}$
for some
![]() $\unicode[STIX]{x1D6E5}$
. Clearly,
$\unicode[STIX]{x1D6E5}$
. Clearly,
If
![]() $R$
is simplicial, an order ideal
$R$
is simplicial, an order ideal
![]() $\unicode[STIX]{x1D6E5}$
is essentially a simplicial complex on the vertices
$\unicode[STIX]{x1D6E5}$
is essentially a simplicial complex on the vertices
![]() $1,2,\ldots ,n$
. If
$1,2,\ldots ,n$
. If
![]() $R$
is the polynomial ring
$R$
is the polynomial ring
![]() $\Bbbk [x_{1},\ldots ,x_{n}]$
, then
$\Bbbk [x_{1},\ldots ,x_{n}]$
, then
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
is nothing but the Stanley–Reisner ring of the simplicial complex
$R/I_{\unicode[STIX]{x1D6E5}}$
is nothing but the Stanley–Reisner ring of the simplicial complex
![]() $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
.
For each
![]() $F\in L$
, take some
$F\in L$
, take some
![]() $\mathbf{c}\,(F)\in C\cap \operatorname{rel - int}(F)$
(i.e.,
$\mathbf{c}\,(F)\in C\cap \operatorname{rel - int}(F)$
(i.e.,
![]() $s(\mathbf{c}\,(F))=F$
). For a squarefree
$s(\mathbf{c}\,(F))=F$
). For a squarefree
![]() $R$
-module
$R$
-module
![]() $M$
and
$M$
and
![]() $F,G\in L$
with
$F,G\in L$
with
![]() $G\supset F$
, [Reference Yanagawa27, Theorem 3.3] gives a
$G\supset F$
, [Reference Yanagawa27, Theorem 3.3] gives a
![]() $\Bbbk$
-linear map
$\Bbbk$
-linear map
These maps satisfy
![]() $\unicode[STIX]{x1D711}_{F,F}^{M}=\operatorname{Id}$
and
$\unicode[STIX]{x1D711}_{F,F}^{M}=\operatorname{Id}$
and
![]() $\unicode[STIX]{x1D711}_{H,G}^{M}\circ \unicode[STIX]{x1D711}_{G,F}^{M}=\unicode[STIX]{x1D711}_{H,F}^{M}$
for all
$\unicode[STIX]{x1D711}_{H,G}^{M}\circ \unicode[STIX]{x1D711}_{G,F}^{M}=\unicode[STIX]{x1D711}_{H,F}^{M}$
for all
![]() $H\supset G\supset F$
. We have
$H\supset G\supset F$
. We have
![]() $M_{\mathbf{c}\,}\cong M_{\mathbf{c}\,^{\prime }}$
for
$M_{\mathbf{c}\,}\cong M_{\mathbf{c}\,^{\prime }}$
for
![]() $\mathbf{c}\,,\mathbf{c}\,^{\prime }\in C$
with
$\mathbf{c}\,,\mathbf{c}\,^{\prime }\in C$
with
![]() $s(\mathbf{c}\,)=s(\mathbf{c}\,^{\prime })$
. Under these isomorphisms, the maps
$s(\mathbf{c}\,)=s(\mathbf{c}\,^{\prime })$
. Under these isomorphisms, the maps
![]() $\unicode[STIX]{x1D711}_{G,F}^{M}$
do not depend on the particular choice of
$\unicode[STIX]{x1D711}_{G,F}^{M}$
do not depend on the particular choice of
![]() $\mathbf{c}\,(F)$
.
$\mathbf{c}\,(F)$
.
Let
![]() $\operatorname{Sq}R$
be the full subcategory of
$\operatorname{Sq}R$
be the full subcategory of
![]() $\operatorname{ \ast mod}R$
consisting of squarefree modules. As shown in [Reference Yanagawa27],
$\operatorname{ \ast mod}R$
consisting of squarefree modules. As shown in [Reference Yanagawa27],
![]() $\operatorname{Sq}R$
is an abelian category with enough injectives. For an indecomposable squarefree module
$\operatorname{Sq}R$
is an abelian category with enough injectives. For an indecomposable squarefree module
![]() $M$
, it is injective in
$M$
, it is injective in
![]() $\operatorname{Sq}R$
if and only if
$\operatorname{Sq}R$
if and only if
![]() $M\cong R/\mathfrak{p}_{F}$
for some
$M\cong R/\mathfrak{p}_{F}$
for some
![]() $F\in L$
.
$F\in L$
.
Let
![]() $\unicode[STIX]{x1D714}_{R}$
be the
$\unicode[STIX]{x1D714}_{R}$
be the
![]() $\mathbb{Z}^{n}$
-graded canonical module of
$\mathbb{Z}^{n}$
-graded canonical module of
![]() $R$
. It is well known that
$R$
. It is well known that
![]() $\unicode[STIX]{x1D714}_{R}$
is isomorphic to the radical monomial ideal
$\unicode[STIX]{x1D714}_{R}$
is isomorphic to the radical monomial ideal
![]() $(\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C,s(\mathbf{c}\,)=P)$
. As shown in [Reference Yanagawa27, Proposition 3.7], we have
$(\mathbf{x}^{\mathbf{c}\,}\mid \mathbf{c}\,\in C,s(\mathbf{c}\,)=P)$
. As shown in [Reference Yanagawa27, Proposition 3.7], we have
![]() $\text{Ext}_{R}^{i}(M,\unicode[STIX]{x1D714}_{R})\in \operatorname{Sq}R$
for
$\text{Ext}_{R}^{i}(M,\unicode[STIX]{x1D714}_{R})\in \operatorname{Sq}R$
for
![]() $M\in \operatorname{Sq}R$
.
$M\in \operatorname{Sq}R$
.
5.1 Lyubeznik numbers
Let
![]() $R=\Bbbk [C]$
be a normal simplicial semigroup ring that is Gorenstein, and let
$R=\Bbbk [C]$
be a normal simplicial semigroup ring that is Gorenstein, and let
![]() $I$
be a monomial ideal of
$I$
be a monomial ideal of
![]() $R$
. As in the polynomial ring case, we set the Lyubeznik numbers as
$R$
. As in the polynomial ring case, we set the Lyubeznik numbers as
Work of the second author in [Reference Yanagawa27] states that this set of invariants are well defined in this framework. Namely, Theorem 4.2 holds verbatim in this situation.
Theorem 5.2. [Reference Yanagawa27, Corollary 5.12]
Let
![]() $R=\Bbbk [C]$
be a normal simplicial semigroup ring that is Gorenstein, and let
$R=\Bbbk [C]$
be a normal simplicial semigroup ring that is Gorenstein, and let
![]() $I_{\unicode[STIX]{x1D6E5}}$
be a radical monomial ideal. Then, we have
$I_{\unicode[STIX]{x1D6E5}}$
be a radical monomial ideal. Then, we have
Notice that in this setting we have that whenever we have a multigraded isomorphism
![]() $\Bbbk [C]/I_{\unicode[STIX]{x1D6E5}}\cong \Bbbk [C^{\prime }]/I_{\unicode[STIX]{x1D6E5}^{\prime }}$
between quotients of Gorenstein normal simplicial semigroup rings by radical monomial ideals, then the corresponding Lyubeznik numbers coincide. This multigraded framework slightly differs from the original situation for regular local rings stated in [Reference Lyubeznik13]. However, as stated in [Reference Yanagawa27, Remark 5.14], if
$\Bbbk [C]/I_{\unicode[STIX]{x1D6E5}}\cong \Bbbk [C^{\prime }]/I_{\unicode[STIX]{x1D6E5}^{\prime }}$
between quotients of Gorenstein normal simplicial semigroup rings by radical monomial ideals, then the corresponding Lyubeznik numbers coincide. This multigraded framework slightly differs from the original situation for regular local rings stated in [Reference Lyubeznik13]. However, as stated in [Reference Yanagawa27, Remark 5.14], if
![]() $\unicode[STIX]{x1D6E5}\cong \unicode[STIX]{x1D6E5}^{\prime }$
as simplicial complexes, then
$\unicode[STIX]{x1D6E5}\cong \unicode[STIX]{x1D6E5}^{\prime }$
as simplicial complexes, then
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
and
$R/I_{\unicode[STIX]{x1D6E5}}$
and
![]() $R^{\prime }/I_{\unicode[STIX]{x1D6E5}^{\prime }}$
have the same Lyubeznik numbers. In this sense, to study the Lyubeznik numbers of a quotient
$R^{\prime }/I_{\unicode[STIX]{x1D6E5}^{\prime }}$
have the same Lyubeznik numbers. In this sense, to study the Lyubeznik numbers of a quotient
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
of a Gorenstein normal simplicial semigroup ring
$R/I_{\unicode[STIX]{x1D6E5}}$
of a Gorenstein normal simplicial semigroup ring
![]() $R$
by a radical monomial ideal
$R$
by a radical monomial ideal
![]() $I_{\unicode[STIX]{x1D6E5}}$
, we may assume that
$I_{\unicode[STIX]{x1D6E5}}$
, we may assume that
![]() $R$
is a polynomial ring and
$R$
is a polynomial ring and
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
is a Stanley–Reisner ring. In Theorem 5.3, we prove a stronger result.
$R/I_{\unicode[STIX]{x1D6E5}}$
is a Stanley–Reisner ring. In Theorem 5.3, we prove a stronger result.
It is also worth pointing out that several features of Lyubeznik numbers are still true in this setting. In what follows, we assume that
![]() $I$
is a monomial ideal of
$I$
is a monomial ideal of
![]() $R$
.
$R$
.
(1) As in the polynomial ring case, we have the Euler characteristic equation
Moreover, the statements corresponding to Theorem 2.1 (the consecutiveness of nontrivial lines) still hold. In fact, we may assume that
![]() $I$
is a radical ideal, and hence
$I$
is a radical ideal, and hence
![]() $I=I_{\unicode[STIX]{x1D6E5}}$
for some simplicial complex
$I=I_{\unicode[STIX]{x1D6E5}}$
for some simplicial complex
![]() $\unicode[STIX]{x1D6E5}$
, and then reduce to the case when
$\unicode[STIX]{x1D6E5}$
, and then reduce to the case when
![]() $R$
is a polynomial ring as in [Reference Yanagawa27, Remark 5.14 (b)].
$R$
is a polynomial ring as in [Reference Yanagawa27, Remark 5.14 (b)].
If we assume that
![]() $I=\sqrt{I}$
, Proposition 4.4 also holds in the present situation. However, we cannot drop this assumption, since we have no idea whether the condition of being sequentially Cohen–Macaulay is preserved after taking radicals. What is known is that if
$I=\sqrt{I}$
, Proposition 4.4 also holds in the present situation. However, we cannot drop this assumption, since we have no idea whether the condition of being sequentially Cohen–Macaulay is preserved after taking radicals. What is known is that if
![]() $R/I$
is Cohen–Macaulay, then so is
$R/I$
is Cohen–Macaulay, then so is
![]() $R/\sqrt{I}$
(see [Reference Yanagawa30, Theorem 6.1]). Hence, if
$R/\sqrt{I}$
(see [Reference Yanagawa30, Theorem 6.1]). Hence, if
![]() $R/I$
is Cohen–Macaulay, then the Lyubeznik table of
$R/I$
is Cohen–Macaulay, then the Lyubeznik table of
![]() $R/I$
is trivial.
$R/I$
is trivial.
(2) For a radical monomial ideal
![]() $I_{\unicode[STIX]{x1D6E5}}$
with
$I_{\unicode[STIX]{x1D6E5}}$
with
![]() $\dim R/I_{\unicode[STIX]{x1D6E5}}=d$
, the highest Lyubeznik number
$\dim R/I_{\unicode[STIX]{x1D6E5}}=d$
, the highest Lyubeznik number
has a simple topological (or combinatorial) meaning. In fact, to study this number, we may assume that
![]() $R$
is a polynomial ring, and we can use a combinatorial description of
$R$
is a polynomial ring, and we can use a combinatorial description of
given in [Reference Stanley22, p. 96]. Roughly speaking,
![]() $\unicode[STIX]{x1D706}_{d,d}(R/I_{\unicode[STIX]{x1D6E5}})$
is the number of “connected in codimension-one components” of
$\unicode[STIX]{x1D706}_{d,d}(R/I_{\unicode[STIX]{x1D6E5}})$
is the number of “connected in codimension-one components” of
![]() $|\unicode[STIX]{x1D6E5}|$
. (This result holds in a much wider context; see [Reference Zhang31].) In particular, if
$|\unicode[STIX]{x1D6E5}|$
. (This result holds in a much wider context; see [Reference Zhang31].) In particular, if
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
satisfies Serre’s condition
$R/I_{\unicode[STIX]{x1D6E5}}$
satisfies Serre’s condition
![]() $(S_{2})$
, then
$(S_{2})$
, then
![]() $\unicode[STIX]{x1D706}_{d,d}(R/I_{\unicode[STIX]{x1D6E5}})=1$
, while the converse is not true.
$\unicode[STIX]{x1D706}_{d,d}(R/I_{\unicode[STIX]{x1D6E5}})=1$
, while the converse is not true.
5.2 Lyubeznik table is a topological invariant
Recall that if
![]() $R=\Bbbk [C]$
is simplicial, then an order ideal
$R=\Bbbk [C]$
is simplicial, then an order ideal
![]() $\unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6E5}$
of
![]() $L$
is essentially a simplicial complex, and hence it has the geometric realization
$L$
is essentially a simplicial complex, and hence it has the geometric realization
![]() $|\unicode[STIX]{x1D6E5}|$
. It is natural to ask how Lyubeznik numbers of
$|\unicode[STIX]{x1D6E5}|$
. It is natural to ask how Lyubeznik numbers of
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
depend on
$R/I_{\unicode[STIX]{x1D6E5}}$
depend on
![]() $|\unicode[STIX]{x1D6E5}|$
. The next theorem shows that Lyubeznik numbers are not only algebraic invariants but also topological invariants.
$|\unicode[STIX]{x1D6E5}|$
. The next theorem shows that Lyubeznik numbers are not only algebraic invariants but also topological invariants.
Theorem 5.3. Let
![]() $R=\Bbbk [C]$
be a simplicial normal semigroup ring that is Gorenstein, and let
$R=\Bbbk [C]$
be a simplicial normal semigroup ring that is Gorenstein, and let
![]() $I_{\unicode[STIX]{x1D6E5}}\subset R$
be a radical monomial ideal. Then,
$I_{\unicode[STIX]{x1D6E5}}\subset R$
be a radical monomial ideal. Then,
![]() $\unicode[STIX]{x1D706}_{p,i}(R/I_{\unicode[STIX]{x1D6E5}})$
depends only on the homeomorphism class of
$\unicode[STIX]{x1D706}_{p,i}(R/I_{\unicode[STIX]{x1D6E5}})$
depends only on the homeomorphism class of
![]() $|\unicode[STIX]{x1D6E5}|$
and
$|\unicode[STIX]{x1D6E5}|$
and
![]() $\operatorname{char}(\Bbbk )$
.
$\operatorname{char}(\Bbbk )$
.
Bearing in mind Theorem 5.2, it suffices to show that
depends only on the topology of
![]() $|\unicode[STIX]{x1D6E5}|$
and
$|\unicode[STIX]{x1D6E5}|$
and
![]() $\operatorname{char}(\Bbbk )$
. For this statement, the assumption that
$\operatorname{char}(\Bbbk )$
. For this statement, the assumption that
![]() $R$
is simplicial and Gorenstein is irrelevant. (If
$R$
is simplicial and Gorenstein is irrelevant. (If
![]() $R$
is not simplicial, then
$R$
is not simplicial, then
![]() $\unicode[STIX]{x1D6E5}$
is essentially a CW complex.) In [Reference Okazaki and Yanagawa19, Theorem 2.10], Okazaki and the second author showed that the invariant that is (essentially) equal to
$\unicode[STIX]{x1D6E5}$
is essentially a CW complex.) In [Reference Okazaki and Yanagawa19, Theorem 2.10], Okazaki and the second author showed that the invariant that is (essentially) equal to
depends only on
![]() $|\unicode[STIX]{x1D6E5}|$
and
$|\unicode[STIX]{x1D6E5}|$
and
![]() $\operatorname{char}(\Bbbk )$
for each
$\operatorname{char}(\Bbbk )$
for each
![]() $i$
. Our proof here uses similar arguments to the aforementioned result. To do so, we have to recall some previous work of the second author in [Reference Yanagawa28].
$i$
. Our proof here uses similar arguments to the aforementioned result. To do so, we have to recall some previous work of the second author in [Reference Yanagawa28].
Recall that
![]() $P=\mathbb{R}_{{\geqslant}0}C$
is a polyhedral cone associated with the semigroup ring
$P=\mathbb{R}_{{\geqslant}0}C$
is a polyhedral cone associated with the semigroup ring
![]() $R=\Bbbk [C]$
. We have a hyperplane
$R=\Bbbk [C]$
. We have a hyperplane
![]() $H\subset \mathbb{R}^{n}$
such that
$H\subset \mathbb{R}^{n}$
such that
![]() $B:=H\cap P$
is an
$B:=H\cap P$
is an
![]() $(n-1)$
-polytope (an
$(n-1)$
-polytope (an
![]() $(n-1)$
-simplex, if
$(n-1)$
-simplex, if
![]() $R$
is simplicial). For
$R$
is simplicial). For
![]() $F\in L$
, set
$F\in L$
, set
![]() $|F|$
to be the relative interior of the face
$|F|$
to be the relative interior of the face
![]() $F\cap H$
of
$F\cap H$
of
![]() $B$
. We can regard an order ideal
$B$
. We can regard an order ideal
![]() $\unicode[STIX]{x1D6E5}\subseteq L$
as a CW complex (a simplicial complex, if
$\unicode[STIX]{x1D6E5}\subseteq L$
as a CW complex (a simplicial complex, if
![]() $R$
is simplicial) whose geometric realization is
$R$
is simplicial) whose geometric realization is
![]() $|\unicode[STIX]{x1D6E5}|:=\bigcup _{F\in \unicode[STIX]{x1D6E5}}|F|\subseteq B$
.
$|\unicode[STIX]{x1D6E5}|:=\bigcup _{F\in \unicode[STIX]{x1D6E5}}|F|\subseteq B$
.
For
![]() $F\in L$
,
$F\in L$
,
is an open set of
![]() $B$
. Note that
$B$
. Note that
![]() $\{U_{F}\mid \{0\}\neq F\in L\}$
is an open covering of
$\{U_{F}\mid \{0\}\neq F\in L\}$
is an open covering of
![]() $B$
. In [Reference Yanagawa28], from
$B$
. In [Reference Yanagawa28], from
![]() $M\in \operatorname{Sq}R$
, we constructed a sheaf
$M\in \operatorname{Sq}R$
, we constructed a sheaf
![]() $M^{+}$
on
$M^{+}$
on
![]() $B$
. More precisely, the assignment
$B$
. More precisely, the assignment
for each
![]() $F\neq \{0\}$
and the map
$F\neq \{0\}$
and the map
for
![]() $F,G\neq \{0\}$
with
$F,G\neq \{0\}$
with
![]() $F\supset G$
(equivalently,
$F\supset G$
(equivalently,
![]() $U_{G}\supset U_{F}$
) define a sheaf. Note that
$U_{G}\supset U_{F}$
) define a sheaf. Note that
![]() $M_{0}$
is irrelevant to
$M_{0}$
is irrelevant to
![]() $M^{+}$
.
$M^{+}$
.
For example,
![]() $(R/I_{\unicode[STIX]{x1D6E5}})^{+}\cong j_{\ast }\text{}\underline{\Bbbk }_{|\unicode[STIX]{x1D6E5}|}$
, where
$(R/I_{\unicode[STIX]{x1D6E5}})^{+}\cong j_{\ast }\text{}\underline{\Bbbk }_{|\unicode[STIX]{x1D6E5}|}$
, where
![]() $\text{}\underline{\Bbbk }_{|\unicode[STIX]{x1D6E5}|}$
is the constant sheaf on
$\text{}\underline{\Bbbk }_{|\unicode[STIX]{x1D6E5}|}$
is the constant sheaf on
![]() $|\unicode[STIX]{x1D6E5}|$
with coefficients in
$|\unicode[STIX]{x1D6E5}|$
with coefficients in
![]() $\Bbbk$
, and
$\Bbbk$
, and
![]() $j$
is the embedding map
$j$
is the embedding map
![]() $|\unicode[STIX]{x1D6E5}|{\hookrightarrow}B$
. Similarly, we have that
$|\unicode[STIX]{x1D6E5}|{\hookrightarrow}B$
. Similarly, we have that
![]() $(\unicode[STIX]{x1D714}_{R})^{+}\cong h_{!}\text{}\underline{\Bbbk }_{B^{\circ }}$
, where
$(\unicode[STIX]{x1D714}_{R})^{+}\cong h_{!}\text{}\underline{\Bbbk }_{B^{\circ }}$
, where
![]() $\text{}\underline{\Bbbk }_{B^{\circ }}$
is the constant sheaf on the relative interior
$\text{}\underline{\Bbbk }_{B^{\circ }}$
is the constant sheaf on the relative interior
![]() $B^{\circ }$
of
$B^{\circ }$
of
![]() $B$
, and
$B$
, and
![]() $h$
is the embedding map
$h$
is the embedding map
![]() $B^{\circ }{\hookrightarrow}B$
. Note that
$B^{\circ }{\hookrightarrow}B$
. Note that
![]() $(\unicode[STIX]{x1D714}_{R})^{+}$
is the orientation sheaf of
$(\unicode[STIX]{x1D714}_{R})^{+}$
is the orientation sheaf of
![]() $B$
with coefficients in
$B$
with coefficients in
![]() $\Bbbk$
.
$\Bbbk$
.
Let
![]() $\unicode[STIX]{x1D6E5}\subseteq L$
be an order ideal, and set
$\unicode[STIX]{x1D6E5}\subseteq L$
be an order ideal, and set
![]() $X:=|\unicode[STIX]{x1D6E5}|\subseteq B$
. For
$X:=|\unicode[STIX]{x1D6E5}|\subseteq B$
. For
![]() $M\in \operatorname{Sq}R$
,
$M\in \operatorname{Sq}R$
,
![]() $M$
is an
$M$
is an
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
-module (i.e.,
$R/I_{\unicode[STIX]{x1D6E5}}$
-module (i.e.,
![]() $\operatorname{ann}(M)\supset I_{\unicode[STIX]{x1D6E5}}$
) if and only if
$\operatorname{ann}(M)\supset I_{\unicode[STIX]{x1D6E5}}$
) if and only if
![]() $\text{Supp}(M^{+}):=\{x\in B\mid (M^{+})_{x}\neq 0\}\subseteq X$
. In this case, we have
$\text{Supp}(M^{+}):=\{x\in B\mid (M^{+})_{x}\neq 0\}\subseteq X$
. In this case, we have
for all
![]() $i$
. Here,
$i$
. Here,
![]() $M^{+}|_{X}$
is the restriction of the sheaf
$M^{+}|_{X}$
is the restriction of the sheaf
![]() $M^{+}$
to the closed set
$M^{+}$
to the closed set
![]() $X\subseteq B$
. Combining this fact with [Reference Yanagawa28, Theorem 3.3], we have the following.
$X\subseteq B$
. Combining this fact with [Reference Yanagawa28, Theorem 3.3], we have the following.
Theorem 5.4. (Cf. [Reference Yanagawa28, Theorem 3.3])
With the above situation, we have
and an exact sequence
In particular,
![]() $[H_{\mathfrak{m}}^{i+1}(R/I_{\unicode[STIX]{x1D6E5}})]_{0}\cong \widetilde{H}^{i}(X;\Bbbk )$
for all
$[H_{\mathfrak{m}}^{i+1}(R/I_{\unicode[STIX]{x1D6E5}})]_{0}\cong \widetilde{H}^{i}(X;\Bbbk )$
for all
![]() $i\geqslant 0$
, where
$i\geqslant 0$
, where
![]() $\widetilde{H}^{i}(X;\Bbbk )$
denotes the
$\widetilde{H}^{i}(X;\Bbbk )$
denotes the
![]() $i$
th reduced cohomology of
$i$
th reduced cohomology of
![]() $X$
with coefficients in
$X$
with coefficients in
![]() $\Bbbk$
.
$\Bbbk$
.
Recall that
![]() $X$
admits Verdier’s dualizing complex
$X$
admits Verdier’s dualizing complex
![]() ${\mathcal{D}}_{X}^{\bullet }$
with coefficients in
${\mathcal{D}}_{X}^{\bullet }$
with coefficients in
![]() $\Bbbk$
. For example,
$\Bbbk$
. For example,
![]() ${\mathcal{D}}_{B}^{\bullet }$
is quasi-isomorphic to
${\mathcal{D}}_{B}^{\bullet }$
is quasi-isomorphic to
![]() $(\unicode[STIX]{x1D714}_{R})^{+}[n-1]$
. The first half of (1) of the next theorem is a restatement of [Reference Yanagawa28, Theorem 4.2], and the rest is that of [Reference Yanagawa30, Lemma 5.11].
$(\unicode[STIX]{x1D714}_{R})^{+}[n-1]$
. The first half of (1) of the next theorem is a restatement of [Reference Yanagawa28, Theorem 4.2], and the rest is that of [Reference Yanagawa30, Lemma 5.11].
Theorem 5.5. [Reference Yanagawa28, Theorem 4.2] and [Reference Yanagawa30, Lemma 5.11]
With the above notation, we have the following.
(1)
 $\text{Supp}(\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+})\subseteq X$
and Moreover, for
$\text{Supp}(\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+})\subseteq X$
and Moreover, for $$\begin{eqnarray}\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+}|_{X}\cong {\mathcal{E}}xt^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+}|_{X}\cong {\mathcal{E}}xt^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet }).\end{eqnarray}$$
 $i\geqslant 2$
, we have
$i\geqslant 2$
, we have  $$\begin{eqnarray}[\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+}]_{0}\cong \text{Ext}^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet }).\end{eqnarray}$$
$$\begin{eqnarray}[\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+}]_{0}\cong \text{Ext}^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet }).\end{eqnarray}$$
(2) Via the isomorphisms in (1), for
 $i\geqslant 2$
, the natural map coincides with the middle map
$i\geqslant 2$
, the natural map coincides with the middle map $$\begin{eqnarray}\text{Ext}^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet })\longrightarrow \unicode[STIX]{x1D6E4}(X;{\mathcal{E}}xt^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet }))\end{eqnarray}$$
of the sequence (5.1) for
$$\begin{eqnarray}\text{Ext}^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet })\longrightarrow \unicode[STIX]{x1D6E4}(X;{\mathcal{E}}xt^{1-i}(M^{+}|_{X},{\mathcal{D}}_{X}^{\bullet }))\end{eqnarray}$$
of the sequence (5.1) for $$\begin{eqnarray}[\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})]_{0}\longrightarrow \unicode[STIX]{x1D6E4}(X;\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+}|_{X})\end{eqnarray}$$
$$\begin{eqnarray}[\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})]_{0}\longrightarrow \unicode[STIX]{x1D6E4}(X;\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})^{+}|_{X})\end{eqnarray}$$
 $\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})\in \operatorname{Sq}R$
.
$\text{Ext}_{R}^{n-i}(M,\unicode[STIX]{x1D714}_{R})\in \operatorname{Sq}R$
.
The Proof of Theorem 5.3.
We show that the dimension of
depends only on
![]() $X$
and
$X$
and
![]() $\operatorname{char}(\Bbbk )$
. If
$\operatorname{char}(\Bbbk )$
. If
![]() $p\geqslant 2$
, then we have
$p\geqslant 2$
, then we have
by Theorems 5.4 and 5.5 (1). The right-hand side of the equation clearly depends only on
![]() $X$
and
$X$
and
![]() $\operatorname{char}(\Bbbk )$
for each
$\operatorname{char}(\Bbbk )$
for each
![]() $p,i$
. Next, we consider the case
$p,i$
. Next, we consider the case
![]() $p=0,1$
. By Theorem 5.4,
$p=0,1$
. By Theorem 5.4,
![]() $H_{\mathfrak{m}}^{0}(\text{Ext}_{R}^{n-i}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R}))$
and
$H_{\mathfrak{m}}^{0}(\text{Ext}_{R}^{n-i}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R}))$
and
![]() $H_{\mathfrak{m}}^{1}(\text{Ext}_{R}^{n-i}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R}))$
are the kernel and the cokernel of the map
$H_{\mathfrak{m}}^{1}(\text{Ext}_{R}^{n-i}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R}))$
are the kernel and the cokernel of the map
respectively. If
![]() $i\geqslant 2$
, the above map is equivalent to the natural map
$i\geqslant 2$
, the above map is equivalent to the natural map
by Theorem 5.5 (2), and the dimensions of its kernel and cokernel are invariants of
![]() $X$
.
$X$
.
It remains to show the case (
![]() $p=0,1$
and)
$p=0,1$
and)
![]() $i=0,1$
. Clearly,
$i=0,1$
. Clearly,
![]() $\text{Ext}_{R}^{n}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R})\neq 0$
if and only if
$\text{Ext}_{R}^{n}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R})\neq 0$
if and only if
![]() $\text{Ext}_{R}^{n}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R})=\Bbbk$
, if and only if
$\text{Ext}_{R}^{n}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R})=\Bbbk$
, if and only if
![]() $I_{\unicode[STIX]{x1D6E5}}=\mathfrak{m}$
, if and only if
$I_{\unicode[STIX]{x1D6E5}}=\mathfrak{m}$
, if and only if
![]() $X=\emptyset$
. Hence,
$X=\emptyset$
. Hence,
![]() $\unicode[STIX]{x1D706}_{0,0}(R/I_{\unicode[STIX]{x1D6E5}})\neq 0$
if and only if
$\unicode[STIX]{x1D706}_{0,0}(R/I_{\unicode[STIX]{x1D6E5}})\neq 0$
if and only if
![]() $\unicode[STIX]{x1D706}_{0,0}(R/I_{\unicode[STIX]{x1D6E5}})=1$
, if and only if
$\unicode[STIX]{x1D706}_{0,0}(R/I_{\unicode[STIX]{x1D6E5}})=1$
, if and only if
![]() $X=\emptyset$
. On the other hand, it is easy to check that
$X=\emptyset$
. On the other hand, it is easy to check that
![]() $\unicode[STIX]{x1D706}_{1,1}(R/I_{\unicode[STIX]{x1D6E5}})$
is always trivial; that is,
$\unicode[STIX]{x1D706}_{1,1}(R/I_{\unicode[STIX]{x1D6E5}})$
is always trivial; that is,
(The same is true for the local ring case using the spectral sequence argument as in the proof of Theorem 2.1 or adapting the techniques used in [Reference Walther24].) Hence, the remaining case is only
![]() $\unicode[STIX]{x1D706}_{0,1}(R/I_{\unicode[STIX]{x1D6E5}})$
, but the following fact holds.
$\unicode[STIX]{x1D706}_{0,1}(R/I_{\unicode[STIX]{x1D6E5}})$
, but the following fact holds.
Claim.
If
![]() $R=\Bbbk [C]$
is a simplicial normal semigroup ring that is Gorenstein, then we have
$R=\Bbbk [C]$
is a simplicial normal semigroup ring that is Gorenstein, then we have
where
![]() $c$
is the number of connected components of
$c$
is the number of connected components of
![]() $|\unicode[STIX]{x1D6E5}^{\prime }|:=|\unicode[STIX]{x1D6E5}|\setminus \{\text{isolated points}\}$
.
$|\unicode[STIX]{x1D6E5}^{\prime }|:=|\unicode[STIX]{x1D6E5}|\setminus \{\text{isolated points}\}$
.
Let us prove the claim. We may assume that
![]() $\dim (R/I_{\unicode[STIX]{x1D6E5}})>0$
. If
$\dim (R/I_{\unicode[STIX]{x1D6E5}})>0$
. If
![]() $\dim (R/I_{\unicode[STIX]{x1D6E5}})=1$
, then
$\dim (R/I_{\unicode[STIX]{x1D6E5}})=1$
, then
![]() $R/I_{\unicode[STIX]{x1D6E5}}$
is Cohen–Macaulay, and the assertion is clear. Therefore, we may assume that
$R/I_{\unicode[STIX]{x1D6E5}}$
is Cohen–Macaulay, and the assertion is clear. Therefore, we may assume that
![]() $\dim (R/I_{\unicode[STIX]{x1D6E5}})\geqslant 2$
. First, we consider the case when
$\dim (R/I_{\unicode[STIX]{x1D6E5}})\geqslant 2$
. First, we consider the case when
![]() $I_{\unicode[STIX]{x1D6E5}}$
does not have one-dimensional associated primes; equivalently,
$I_{\unicode[STIX]{x1D6E5}}$
does not have one-dimensional associated primes; equivalently,
![]() $|\unicode[STIX]{x1D6E5}|$
does not admit isolated points (i.e.,
$|\unicode[STIX]{x1D6E5}|$
does not admit isolated points (i.e.,
![]() $|\unicode[STIX]{x1D6E5}|=|\unicode[STIX]{x1D6E5}^{\prime }|$
). Then, we have
$|\unicode[STIX]{x1D6E5}|=|\unicode[STIX]{x1D6E5}^{\prime }|$
). Then, we have
Since
![]() $\text{Ext}_{R}^{n-1}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R})$
is a squarefree module, we have
$\text{Ext}_{R}^{n-1}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R})$
is a squarefree module, we have
We also have
where the second isomorphism follows from the last statement of Theorem 5.4. Hence,
and we are done.
Therefore, we now consider the case where
![]() $I_{\unicode[STIX]{x1D6E5}}$
admits one-dimensional associated primes. Set
$I_{\unicode[STIX]{x1D6E5}}$
admits one-dimensional associated primes. Set
![]() $I:=I_{\unicode[STIX]{x1D6E5}^{\prime }}$
. Then, there is a monomial ideal
$I:=I_{\unicode[STIX]{x1D6E5}^{\prime }}$
. Then, there is a monomial ideal
![]() $J$
of
$J$
of
![]() $R$
with
$R$
with
![]() $I_{\unicode[STIX]{x1D6E5}}=I\cap J$
and
$I_{\unicode[STIX]{x1D6E5}}=I\cap J$
and
![]() $\dim R/J=1$
. Note that
$\dim R/J=1$
. Note that
![]() $I+J=\mathfrak{m}$
. The short exact sequence
$I+J=\mathfrak{m}$
. The short exact sequence
![]() $0\rightarrow R/I_{\unicode[STIX]{x1D6E5}}\rightarrow R/I\oplus R/J\rightarrow R/\mathfrak{m}\,(\cong \Bbbk )\rightarrow 0$
yields the exact sequence
$0\rightarrow R/I_{\unicode[STIX]{x1D6E5}}\rightarrow R/I\oplus R/J\rightarrow R/\mathfrak{m}\,(\cong \Bbbk )\rightarrow 0$
yields the exact sequence
Since Lyubeznik numbers of type
![]() $\unicode[STIX]{x1D706}_{1,1}(-)$
are always trivial, we have
$\unicode[STIX]{x1D706}_{1,1}(-)$
are always trivial, we have
and
![]() $[\text{Ext}_{R}^{n-1}(\text{Ext}_{R}^{n-1}(R/J,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}=\Bbbk$
. It is also clear that
$[\text{Ext}_{R}^{n-1}(\text{Ext}_{R}^{n-1}(R/J,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}=\Bbbk$
. It is also clear that
Thus, applying
![]() $\text{Ext}_{R}^{\bullet }(-,\unicode[STIX]{x1D714}_{R})$
to (5.2), we obtain
$\text{Ext}_{R}^{\bullet }(-,\unicode[STIX]{x1D714}_{R})$
to (5.2), we obtain
 $$\begin{eqnarray}\displaystyle 0 & \longrightarrow & \displaystyle [\text{Ext}_{R}^{n-1}(\text{Ext}_{R}^{n-1}(R/J,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}~(\cong \Bbbk )\longrightarrow [\text{Ext}_{R}^{n}(\Bbbk ,\unicode[STIX]{x1D714}_{R})]_{0}~(\cong \Bbbk )\nonumber\\ \displaystyle & \longrightarrow & \displaystyle [\text{Ext}_{R}^{n}(\text{Ext}_{R}^{n-1}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\nonumber\\ \displaystyle & \longrightarrow & \displaystyle [\text{Ext}_{R}^{n}(\text{Ext}_{R}^{n-1}(R/I,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\longrightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \longrightarrow & \displaystyle [\text{Ext}_{R}^{n-1}(\text{Ext}_{R}^{n-1}(R/J,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}~(\cong \Bbbk )\longrightarrow [\text{Ext}_{R}^{n}(\Bbbk ,\unicode[STIX]{x1D714}_{R})]_{0}~(\cong \Bbbk )\nonumber\\ \displaystyle & \longrightarrow & \displaystyle [\text{Ext}_{R}^{n}(\text{Ext}_{R}^{n-1}(R/I_{\unicode[STIX]{x1D6E5}},\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\nonumber\\ \displaystyle & \longrightarrow & \displaystyle [\text{Ext}_{R}^{n}(\text{Ext}_{R}^{n-1}(R/I,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\longrightarrow 0.\nonumber\end{eqnarray}$$
Since
![]() $[\text{Ext}_{R}^{n}(\text{Ext}_{R}^{n-1}(R/I,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\cong \Bbbk ^{c-1}$
, as we have shown above, it follows that
$[\text{Ext}_{R}^{n}(\text{Ext}_{R}^{n-1}(R/I,\unicode[STIX]{x1D714}_{R}),\unicode[STIX]{x1D714}_{R})]_{0}\cong \Bbbk ^{c-1}$
, as we have shown above, it follows that
and we are done. ◻
Example 5.6. This example concerns the final step of the proof of Theorem 5.3. Let
![]() $R=\Bbbk [x_{1},\ldots ,x_{7}]$
be a polynomial ring, and consider the monomial ideal
$R=\Bbbk [x_{1},\ldots ,x_{7}]$
be a polynomial ring, and consider the monomial ideal
Then,
![]() $|\unicode[STIX]{x1D6E5}|$
consists of one isolated point and three segments; see Figure 1. Therefore,
$|\unicode[STIX]{x1D6E5}|$
consists of one isolated point and three segments; see Figure 1. Therefore,
![]() $|\unicode[STIX]{x1D6E5}^{\prime }|$
, which is
$|\unicode[STIX]{x1D6E5}^{\prime }|$
, which is
![]() $|\unicode[STIX]{x1D6E5}|\setminus \{v_{1}\}$
, consists of three segments. We have
$|\unicode[STIX]{x1D6E5}|\setminus \{v_{1}\}$
, consists of three segments. We have
![]() $\unicode[STIX]{x1D706}_{0,1}(R/I_{\unicode[STIX]{x1D6E5}})=3-1=2$
.
$\unicode[STIX]{x1D706}_{0,1}(R/I_{\unicode[STIX]{x1D6E5}})=3-1=2$
.
Figure 1.
![]() $\unicode[STIX]{x1D6E5}$
in Example 5.6.
$\unicode[STIX]{x1D6E5}$
in Example 5.6.