Article contents
Time, Bohm's Theory, and Quantum Cosmology
Published online by Cambridge University Press: 01 April 2022
Extract
One of the problems of quantum cosmology follows from the fact that the Hamiltonian H of classical general relativity equals zero. Quantizing canonically in the Schrodinger picture, the Schrodinger equation for the wave function Ψ of the universe is therefore the so-called Wheeler-DeWitt equation
 (where Ĥ is the operator version of H) and we have no quantum dynamics. In particular, it follows directly that, if Ȓ is the operator representing the radius of the universe,
(where Ĥ is the operator version of H) and we have no quantum dynamics. In particular, it follows directly that, if Ȓ is the operator representing the radius of the universe,
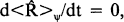 where <Ȓ>ψ = Ψ<|Ȓ|>Ψ, for every Ψ. The universe described by (1) does not expand. But worse still is the fact that there is no time development, contrary to our experience. Like a particle in an eigenstate of zero energy, the state of the universe does not change. The still universe resulting from (1) is a manifestation of the more general “problem of time” afflicting canonical quantum gravity. Despite rare claims to the contrary, most consider it to be a serious difficulty for quantum cosmology.
where <Ȓ>ψ = Ψ<|Ȓ|>Ψ, for every Ψ. The universe described by (1) does not expand. But worse still is the fact that there is no time development, contrary to our experience. Like a particle in an eigenstate of zero energy, the state of the universe does not change. The still universe resulting from (1) is a manifestation of the more general “problem of time” afflicting canonical quantum gravity. Despite rare claims to the contrary, most consider it to be a serious difficulty for quantum cosmology.
- Type
- Research Article
- Information
- Copyright
- Copyright © Philosophy of Science Association 1996
Footnotes
Send reprint requests to the authors, Department of Philosophy, PO Box 270, Rutgers University, New Brunswick, NJ 08903–0270.
References
- 5
- Cited by


