Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-27T17:05:29.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme Behaviors of the Tail Gini-Type Variability Measures

Published online by Cambridge University Press:  23 September 2022

Hongfang Sun  and
Yu Chen Open the ORCID record for Yu Chen [Opens in a new window]
Hongfang Sun
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, China. E-mail: cyu@ustc.edu.cn
Yu Chen
Affiliation:
Department of Statistics and Finance, School of Management, University of Science and Technology of China, Hefei, China. E-mail: cyu@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

For a bivariate random vector 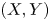$(X, Y)$, suppose 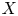$X$ is some interesting loss variable and 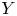$Y$ is a benchmark variable. This paper proposes a new variability measure called the joint tail-Gini functional, which considers not only the tail event of benchmark variable 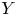$Y$, but also the tail information of 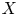$X$ itself. It can be viewed as a class of tail Gini-type variability measures, which also include the recently proposed tail-Gini functional. It is a challenging and interesting task to measure the tail variability of 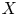$X$ under some extreme scenarios of the variables by extending the Gini's methodology, and the two tail variability measures can serve such a purpose. We study the asymptotic behaviors of these tail Gini-type variability measures, including tail-Gini and joint tail-Gini functionals. The paper conducts this study under both tail dependent and tail independent cases, which are modeled by copulas with so-called tail order property. Some examples are also shown to illuminate our results. In particular, a generalization of the joint tail-Gini functional is considered to provide a more flexible version.

Keywords

Joint tail-Gini functionalRegular variationTail dependenceTail measure of variability
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 37 , Issue 4 , October 2023 , pp. 928 - 942
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asimit, A.V. & Li, J. (2018). Measuring the tail risk: An asymptotic approach. Journal of Mathematical Analysis and Applications 463: 176–197.CrossRefGoogle Scholar
Berkhouch, M., Lakhnati, G., & Righi, M.B. (2018). Extended Gini-type measures of risk and variability. Applied Mathematical Finance 25: 295–314.CrossRefGoogle Scholar
Bingham, N.H., Goldie, C.M., & Teugels, J.L. (1987). Regular variation. In Encyclopedia of mathematics and its applications, vol. 27. Cambridge: Cambridge University Press.Google Scholar
Cai, J. & Li, H. (2005). Conditional tail expectations for multivariate phase-type distributions. Journal of Applied Probability 42: 810–825.CrossRefGoogle Scholar
Cai, J. & Musta, M. (2020). Estimation of the marginal expected shortfall under asymptotic independence. Scandinavian Journal of Statistics 47: 56–83.CrossRefGoogle Scholar
Cai, J., Einmahl, J.H., Haan, L., & Zhou, C. (2015). Estimation of the of the marginal expected shortfall: the mean when a related variable is extreme. Journal of the Royal Statistical Society: Series B 77: 417–442.CrossRefGoogle Scholar
Das, B. & Fasen-Hartmann, V. (2018). Risk contagion under regular variation and asymptotic tail independence. Journal of Multivariate Analysis 165: 194–215.CrossRefGoogle Scholar
de Haan, L. & Ferreira, A. (2006). Extreme value theory: An introduction. New York: Springer.CrossRefGoogle Scholar
Draisma, G., Drees, H., Ferreira, A., & de Haan, L. (2004). Bivariate tail estimation: Dependence in asymptotic independence. Bernoulli 10: 251–280.CrossRefGoogle Scholar
Fisher, R.A. & Tippett, L.H.C. (1928). Limiting forms of the frequency distribution of the largest or smallest member of a sample. In Mathematical Proceedings of the Cambridge Philosophical Society, vol. 24. Cambridge University Press, pp. 180–190.CrossRefGoogle Scholar
Furman, E., Wang, R., & Zitikis, R. (2017). Gini-type measures of risk and variability: Gini shortfall, capital allocations, and heavy-tailed risks. Journal of Banking and Finance 83: 70–84.CrossRefGoogle Scholar
Gini, C. (1912). Variabilità e mutabilità. Bologna: Tipografia di Paolo Cuppin.Google Scholar
Hou, Y. & Wang, X. (2021). Extreme and inference for tail Gini functional with applications in tail risk measurement. Journal of the American Statistical Association 535: 1428–1443.CrossRefGoogle Scholar
Hua, L. & Joe, H. (2011). Tail order and intermediate tail dependence of multivariate copulas. Journal of Multivariate Analysis 102(10): 1454–1471.CrossRefGoogle Scholar
Ji, L., Tan, K., & Yang, F. (2021). Tail dependence and heavy tailedness in extreme risks. Insurance: Mathematics and Economics 99: 282–293.Google Scholar
Kulik, R. & Soulier, P. (2015). Heavy tailed time series with extremal independence. Extremes 18: 273–299.CrossRefGoogle Scholar
Ledford, A.W. & Tawn, J.A. (1996). Statistics for near independence in multivariate extreme values. Biometrika 83: 169–187.CrossRefGoogle Scholar
Li, H. & Li, X. (2013). Stochastic orders in reliability and risk. New York: Springer.CrossRefGoogle Scholar
Nelsen, R.B. (2007). An introduction to copulas. New york: Springer.Google Scholar
Sklar, A. (1959). Fonctions de répartition à n dimensions et leurs marges. Publications de l'Institut de Statistique de L'Université de Paris, vol. 8, pp. 229–231.Google Scholar
Yitzhaki, S. & Schechtman, E. (2012). The Gini methodology: a primer on a statistical methodology, vol. 272. New York: Springer.Google Scholar