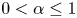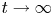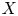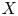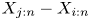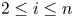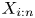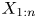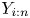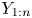Contents
Research Article
Valuing vulnerable Asian options with liquidity risk under Lévy processes
-
- Published online by Cambridge University Press:
- 07 February 2022, pp. 653-673
-
- Article
- Export citation
Ordered multi-state system signature and its dynamic version in evaluating used multi-state systems
-
- Published online by Cambridge University Press:
- 27 July 2022, pp. 873-887
-
- Article
- Export citation
Ordering and aging properties of systems with dependent components governed by the Archimedean copula
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2021, pp. 1-28
-
- Article
- Export citation
Introduction
Preface
-
- Published online by Cambridge University Press:
- 03 April 2023, pp. 322-323
-
- Article
- Export citation
Research Article
Optimal allocation of a coherent system with statistical dependent subsystems
-
- Published online by Cambridge University Press:
- 24 September 2021, pp. 29-48
-
- Article
- Export citation
Optimal management and valuation of a natural resource: the case of optimal harvesting
-
- Published online by Cambridge University Press:
- 11 March 2022, pp. 674-694
-
- Article
- Export citation
Almost first-order stochastic dominance by distorted expectations
- Part of:
-
- Published online by Cambridge University Press:
- 12 August 2022, pp. 888-906
-
- Article
- Export citation
Gerber-Shiu analysis in the compound Poisson model with constant inter-observation times
-
- Published online by Cambridge University Press:
- 06 June 2022, pp. 324-356
-
- Article
- Export citation
On approximation of the analytic fixed finite time large t probability distributions in an extreme renewal process with no-mean inter-renewals
-
- Published online by Cambridge University Press:
- 20 May 2022, pp. 695-710
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Applications of the classical compound Poisson model with claim sizes following a compound distribution
-
- Published online by Cambridge University Press:
- 14 July 2022, pp. 357-386
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The value of information and efficient switching in channel selection
-
- Published online by Cambridge University Press:
- 25 August 2022, pp. 907-927
-
- Article
- Export citation
Star-shaped order for distributions characterized by several parameters and some applications
-
- Published online by Cambridge University Press:
- 28 September 2021, pp. 49-59
-
- Article
- Export citation
Nonlinear and unbalanced urn models with two types of strategies: a stochastic approximation point of view
-
- Published online by Cambridge University Press:
- 20 May 2022, pp. 711-729
-
- Article
- Export citation
Joint moments of discounted claims and discounted perturbation until ruin in the compound Poisson risk model with diffusion
-
- Published online by Cambridge University Press:
- 31 March 2022, pp. 387-417
-
- Article
- Export citation
Covariances in Pólya urn schemes
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2021, pp. 60-71
-
- Article
- Export citation
Extreme Behaviors of the Tail Gini-Type Variability Measures
-
- Published online by Cambridge University Press:
- 23 September 2022, pp. 928-942
-
- Article
- Export citation
Dependence comparisons of order statistics in the proportional hazards model
-
- Published online by Cambridge University Press:
- 21 April 2022, pp. 730-736
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preservation properties of some reliability classes by lifetimes of coherent and mixed systems and their signatures
-
- Published online by Cambridge University Press:
- 23 September 2022, pp. 943-960
-
- Article
- Export citation
Nonparametric estimation of some dividend problems in the perturbed compound Poisson model
-
- Published online by Cambridge University Press:
- 09 September 2022, pp. 418-441
-
- Article
-
- You have access
- HTML
- Export citation
Mean residual life order among largest order statistics arising from resilience-scale models with reduced scale parameters
-
- Published online by Cambridge University Press:
- 22 November 2022, pp. 72-85
-
- Article
- Export citation