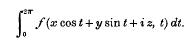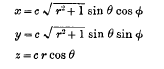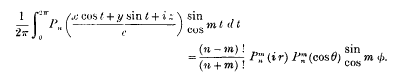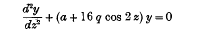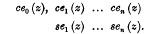Syllabus of papers
Thirty-Third Session, 1914–1915
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. v-vi
-
- Article
-
- You have access
- Export citation
Presents to the library
Presents to the library
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. vii-viii
-
- Article
-
- You have access
- Export citation
Office bearers
Office Bearers
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 1
-
- Article
-
- You have access
- Export citation
Research Article
The Elliptic Cylinder Functions of the Second Kind
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 2-13
-
- Article
-
- You have access
- Export citation
On a class of Differential Equations whose solutions satisfy Integral Equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 14-23
-
- Article
-
- You have access
- Export citation
Easy Proof of Von Staudt's Theorem
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 24
-
- Article
-
- You have access
- Export citation
The Convergence of the Series in Mathieu's Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 25-30
-
- Article
-
- You have access
- Export citation
Note on Suspension Bridge Catenaries
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-34
-
- Article
-
- You have access
- Export citation
On a Class of Integral Equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 35-41
-
- Article
-
- You have access
- Export citation
A Theorem on the Contact of Circles leading up to the Theorems of Feuerbach and Hart
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 42-47
-
- Article
-
- You have access
- Export citation
On the Roots of Confluent Hypergeometric Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 48-64
-
- Article
-
- You have access
- Export citation
On Spheroidal Harmonics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 65-68
-
- Article
-
- You have access
- Export citation
Two remarkable Cubics associated with a Triangle
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 69-84
-
- Article
-
- You have access
- Export citation
Taylor's Cubics associated with a Triangle in Non-Euclidean Geometry
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 85-99
-
- Article
-
- You have access
- Export citation
Quaternion Demonstration of the Theorem of Moments in Rigid Dynamics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 100-102
-
- Article
-
- You have access
- Export citation
On the Roots of a Derivative of a Rational Function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 103-106
-
- Article
-
- You have access
- Export citation
Recurrence Formulae for the Functions which represent Solutions of the Differential Equation:
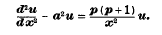
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 107-117
-
- Article
-
- You have access
- Export citation
On Spheroidal Harmonics and Allied Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 118-121
-
- Article
-
- You have access
- Export citation
Determinants connected with the Periodic Solutions of Mathieu's Equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 122-138
-
- Article
-
- You have access
- Export citation
On the Oscillation Functions derived from a Discontinuous Function
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 139-142
-
- Article
-
- You have access
- Export citation




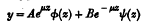
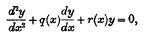
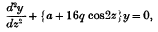
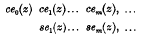
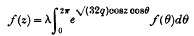
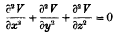
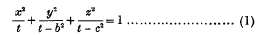
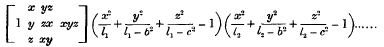
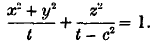
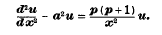
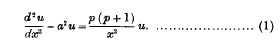
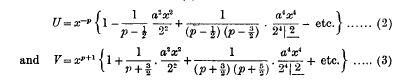
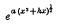 and of
and of 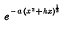 satisfy equation (1) when
satisfy equation (1) when