Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T21:42:09.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations

Part of: Elliptic equations and systems Equations of mathematical physics and other areas of application Partial differential equations

Published online by Cambridge University Press:  11 March 2024

Chunyu Lei  and
Binlin Zhang
Chunyu Lei
Affiliation:
School of Mathematical Sciences, Guizhou Minzu University, Guiyang 550025, P.R. China (leichygzu@sina.cn)
Binlin Zhang
Affiliation:
College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590, P.R. China (zhangbinlin2012@163.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we are concerned with the ground states of the following planar Kirchhoff-type problem: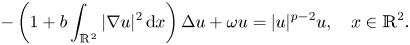

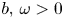\[ -\left(1+b\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \quad x\in\mathbb{R}^2. \]
where $b,\, \omega >0$ are constants, $p>2$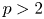. Based on variational methods, regularity theory and Schwarz symmetrization, the equivalence of ground state solutions for the above problem with the minimizers for some minimization problems is obtained. In particular, a new scale technique, together with Lagrange multipliers, is delicately employed to overcome some intrinsic difficulties.

Keywords

Kirchhoff type equationsground state solutionsspherical symmetric

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35A23: Inequalities involving derivatives and differential and integral operators, inequalities for integrals 35Q55: NLS-like equations (nonlinear Schrödinger) 35J61: Semilinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 22
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Autuori, G., Fiscella, A. and Pucci, P.. Stationary Kirchhoff problems involving a fractional elliptic operator and a critical nonlinearity. Nonlinear Anal. 125 (2015), 699–714.CrossRefGoogle Scholar
Berestycki, H., Gallouët, T. and Kavian, O.. Équations de champs scalaires euclidiens non linéaires dans le plan. C. R. Acad. Sci. Paris Sér. I Math. 297 (1983), 307–310.Google Scholar
Berestycki, H. and Lions, P. L.. Nonlinear scalar field equations. Arch. Ration. Mech. AnaI. 82 (1983), 313–375.CrossRefGoogle Scholar
Cazenave, T.. Semilinear Schrödinger Equations, Courant Lecture Notes in Mathematics, Vol. 10 (Providence, RI: American Mathematical Society, 2003).CrossRefGoogle Scholar
Chen, C., Kuo, Y. and Wu, T.. The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions. J. Differ. Equ. 250 (2011), 1876–1908.CrossRefGoogle Scholar
Chen, J. and Yu, F.. On a nonhomogeneous Kirchhoff-type elliptic problem with critical exponential in dimension two. Appl. Anal. 101 (2022), 421–436.CrossRefGoogle Scholar
Deng, Y., Peng, S. and Shuai, W.. Existence and asymptotic behavior of nodal solutions for the Kirchhoff-type problems in $\mathbb {R}^3$. J. Funct. Anal. 269 (2015), 3500–3527.CrossRefGoogle Scholar
Figueiredo, G. M., Ikoma, N. and Júnior, J. R. S.. Existence and concentration result for the Kircchhoff type equations with general nonlinearities. Arch. Ration. Mech. Anal. 213 (2014), 931–979.CrossRefGoogle Scholar
Figueiredo, G. M. and Jünior, J. R. S.. Multiplicity and concentration behavior of positive solutions for a Schrödinger–Kircchhoff type problem via penalization method. ESAIM Control Optim. Calc. Var. 20 (2014), 389–415.CrossRefGoogle Scholar
Gidas, B., Ni, W. and Nirenberg, L., Symmetry of positive solutions of nonlinear elliptic equations in $\mathbb {R}^n$. Mathematical analysis and applications, Part A, Advances in Mathematics Supplementary Studies, Vol. 7. (Academic, New York–London, 1981), pp. 369–402.Google Scholar
He, X. and Zou, W.. Existence and concentration of positive solutions for a Kirchhoff equation in $\mathbb {R}^3$. J. Differ. Equ. 252 (2012), 1813–1834.CrossRefGoogle Scholar
He, Y., Li, G. and Peng, S.. Concentrating bound states for Kirchhoff type problems in $\mathbb {R}^3$ involving critical Sobolev exponents. Adv. Nonlinear Stud. 14 (2014), 441–468.CrossRefGoogle Scholar
Huang, Y., Liu, Z. and Wu, Y.. On Kirchhoff type equations with critical Sobolev exponent. J. Math. Anal. Appl. 462 (2018), 483–504.CrossRefGoogle Scholar
Ikoma, N.. Existence of ground state solutions to the the nonlinear Kirchhoff type equations with potentials. Discrete Contin. Dyn. Syst. 35 (2015), 943–966.CrossRefGoogle Scholar
Jünior, J. R. S. and Siciliano, G.. Positive solutions for a Kirchhoff problem with vanishing nonlocal term. J. Differ. Equ. 265 (2018), 2034–2043.CrossRefGoogle Scholar
Jin, J. and Wu, X.. Infinitely many radial solutions for Kirchhoff-type problems in $\mathbb {R}^N$. J. Math. Anal. Appl. 369 (2010), 564–574.CrossRefGoogle Scholar
Kirchhoff, G.. Mechanik (Leipzig: Teabnes, 1883).Google Scholar
Kwong, M. K.. Uniqueness of positive solutions of $-\Delta u-u+u^p=0$ in $\mathbb {R}^n$. Arch. Ration. Mech. Anal. 105 (1989), 243–266.CrossRefGoogle Scholar
Li, G., Luo, P., Peng, S., Wang, C. H. and Xiang, C. L.. A singularly perturbed Kirchhoff problem revisited. J. Differ. Equ. 268 (2020), 541–589.CrossRefGoogle Scholar
Li, G. and Ye, H. Y.. Existence of positive solutions for nonlinear Kirchhoff type equations in $\mathbb {R}^3$ with critical Sobolev exponent. Math. Meth. Appl. Sci. 37 (2014), 2570–2584.CrossRefGoogle Scholar
Li, Y., Li, F. and Shi, J.. Existence of a positive solution to Kirchhoff type problems without compactness conditions. J. Differ. Equ. 253 (2012), 2285–2294.CrossRefGoogle Scholar
Lions, J. L., On some questions in boundary value problems of mathematical physics. In Contemporary Developments in Continuum Methanics and Partial Differential Equations, Proc. Internat. Sympos. Inst. Mat. Univ. Fed. Rio de Janeiro (1997), Vol. 30, (North-Holland Math. Stud, 1978), pp. 284–346.Google Scholar
Liu, J., Hou, A. and Liao, J.. Multiplicity of positive solutions for a class of singular elliptic equations with critical Sobolev exponent and Kirchhoff-type nonlocal term. Electron. J. Qual. Theory Differ. Equ. 100 (2018), 1–20.CrossRefGoogle Scholar
Naimen, D.. The critical problem of Kirchhoff type elliptic equations in dimension four. J. Differ. Equ. 257 (2014), 1168–1193.CrossRefGoogle Scholar
Perera, K. and Zhang, Z.. Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differ. Equ. 221 (2006), 246–255.CrossRefGoogle Scholar
Qi, S. and Zou, W.. Exact number of positive solutions for the Kirchhoff equation. SIAM J. Math. Anal. 54 (2022), 5424–5446.CrossRefGoogle Scholar
Wang, J., Tian, L., Xu, J. and Zhang, F.. Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth. J. Differ. Equ. 253 (2012), 2314–2351.CrossRefGoogle Scholar
Wang, L., Xie, K. and Zhang, B.. Existence and multiplicity of solutions for critical Kirchhoff-type $p$-Laplacian problems. J. Math. Anal. Appl. 458 (2018), 361–378.CrossRefGoogle Scholar
Wei, J., Tang, X. and Zhang, L., Ground state solutions for planar periodic Kirchhoff type equation with critical exponential growth. Math. Methods Appl. Sci. https://doi.org/10.1002/mma.8308.Google Scholar