Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-25T16:58:15.425Z Has data issue: false hasContentIssue false
  • English
  • Français

On large solutions for fractional Hamilton–Jacobi equations

Part of: Representations of solutions Partial differential equations Miscellaneous topics - Partial differential equations General first-order equations and systems

Published online by Cambridge University Press:  11 July 2023

Gonzalo Dávila ,
Alexander Quaas  and
Erwin Topp
Gonzalo Dávila
Affiliation:
Departamento de Matemática, Universidad Técnica Federico Santa María, Casilla: v-110, Avda. España 1680, Valparaíso, Chile (gonzalo.davila@usm.cl; alexander.quaas@usm.cl)
Alexander Quaas
Affiliation:
Departamento de Matemática, Universidad Técnica Federico Santa María, Casilla: v-110, Avda. España 1680, Valparaíso, Chile (gonzalo.davila@usm.cl; alexander.quaas@usm.cl)
Erwin Topp
Affiliation:
Departamento de Matemática y C.C., Universidad de Santiago de Chile, Casilla 307 Santiago, 454003, Chile Instituto de Matemática, Universidade Federal do Rio de Janeiro, Rio de Janeiro, RJ 21941-909, Brazil (erwin.topp@usach.cl)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the existence of large solutions for nonlocal Dirichlet problems posed on a bounded, smooth domain, associated with fully nonlinear elliptic equations of order $2\,s$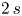, with $s\in (1/2,\,1)$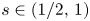, and a coercive gradient term with subcritical power $0< p<2\,s$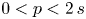. Due to the nonlocal nature of the diffusion, new blow-up phenomena arise within the range $0< p<2\,s$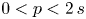, involving a continuum family of solutions and/or solutions blowing-up to $-\infty$ 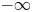on the boundary. This is in striking difference with the local case studied by Lasry–Lions for the subquadratic case $1< p<2$.

Keywords

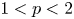Dirichlet problemHamilton–Jacobi equationslarge solutionsnonlocal operatorviscosity solutions

MSC classification

Primary: 35F21: Hamilton-Jacobi equations
Secondary: 35R11: Fractional partial differential equations 35B44: Blow-up 35B40: Asymptotic behavior of solutions 35D40: Viscosity solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 23
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abatangelo, N.. Large $s$-harmonic functions and boundary blow-up solutions for the fractional laplacian. Discrete Contin. Dyn. Syst. 35 (2015), 5555–5607.CrossRefGoogle Scholar
Alarcón, S., García-Melián, J. and Quaas, A.. Keller–Osserman type conditions for some elliptic problems with gradient terms. J. Differ. Equ. 252 (2012), 886–914.CrossRefGoogle Scholar
Barles, G., Chasseigne, E. and Imbert, C.. On the Dirichlet problem for second order elliptic integro-differential equations. Indiana Univ. Math. J. 57 (2008), 213–246.CrossRefGoogle Scholar
Guy, B., Emmanuel, C. and Cyril, I.. Hölder continuity of solutions of second-order non-linear elliptic integro-differential equations. J. Eur. Math. Soc. (JEMS) 13 (2011), 1–26.Google Scholar
Bertoin, J.. Levy processes, Cambridge Tracts in Mathematics, Vol. 121 (Cambridge University Press, Cambridge, 1996).Google Scholar
Caffarelli, L. and Silvestre, L.. Regularity theory for fully nonlinear integro-differential equations. Communicat. Pure Appl. Math. 62 (2009), 597–638.CrossRefGoogle Scholar
Chen, H. and Lv, G.. Boundary blow-up solutions to nonlocal elliptic equations with gradient nonlinearity. Communicat. Contemporary Math. 19 (2017), 1650051.CrossRefGoogle Scholar
Chen, H., Hajaiej, Y. and Wang, H.. Boundary blow-up solutions to fractional elliptic equations in a measure framework. Discrete Continuous Dynam. Syst. - A 36 (2016), 1881–1903.Google Scholar
Chen, H., Felmer, P. and Quaas, A.. Large solutions to elliptic equations involving fractional Laplacian. Ann. Inst. Henri Poincare Analyse non lineaire 32 (2015), 1199–1228.CrossRefGoogle Scholar
Chen, H. and Veron, L.. Semilinear fractional elliptic equations with gradient nonlinearity involving measures. J. Funct. Anal. 266 (2014), 5467–5492.CrossRefGoogle Scholar
Dávila, G., Quaas, A. and Topp, E.. Continuous viscosity solutions for nonlocal Dirichlet problems with coercive gradient terms. Math. Annalen 369 (2017), 1211–1236.CrossRefGoogle Scholar
Di Neza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Lasry, J. M. and Lions, P. L.. Nonlinear elliptic equations with singular boundary conditions and stochastic control with state constraints. Math. Ann. 283 (1989), 583–630.CrossRefGoogle Scholar
Keller, J. B.. On solutions of $\Delta u = f (u)$. Comm. Pure Appl. Math. 10 (1957), 503–510.CrossRefGoogle Scholar
Osserman, R.. On the inequality $\Delta u = f (u)$. Pacific J. Math. 7 (1957), 1641–1647.CrossRefGoogle Scholar
Pham, H.. Optimal stopping of controlled jump diffusion processes: a viscosity solution approach. J. Math. Systems Estim. Control 8 (1998), 27.Google Scholar
Ros-Oton, X. and Serra, J.. Boundary regularity for fully nonlinear integro-differential equations. Duke Math. J. 165 (2016), 2079–2154.CrossRefGoogle Scholar
Sato, K.-I.. Levy Processes and Infinitely Divisible Distributions (Cambridge University Press, Cambridge, 1999).Google Scholar
Topp, E.. Existence and uniqueness for integro-differential equations with dominating drift terms. Comm. Partial Differ. Equ. 39 (2014), 1523–1554.CrossRefGoogle Scholar