Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-12T10:21:42.831Z Has data issue: false hasContentIssue false
  • English
  • Français

On the macroscopic modelling of dilute emulsions under flow

Published online by Cambridge University Press:  13 October 2017

Paul M. Mwasame ,
Norman J. Wagner  and
Antony N. Beris Open the ORCID record for Antony N. Beris [Opens in a new window]
Paul M. Mwasame
Affiliation:
Center for Molecular and Engineering Thermodynamics, Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716, USA
Norman J. Wagner
Affiliation:
Center for Molecular and Engineering Thermodynamics, Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716, USA
Antony N. Beris*
Affiliation:
Center for Molecular and Engineering Thermodynamics, Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE 19716, USA
*
†Email address for correspondence: beris@udel.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A new macroscopic model describing the rheology and microstructure of dilute emulsions with droplet morphology is developed based on an internal contravariant conformation tensor variable which is physically identified with the deformed ellipsoidal geometry of the dispersed phase. The model is consistent with existing first-order capillary number, 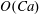$O(Ca)$, theory describing the microstructure as well as 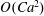$O(Ca^{2})$ theory describing the emulsion-contributed extra stress. These asymptotic solutions are also used to determine all of the model parameters, making it the only macroscopic emulsion model that is consistent with all available asymptotic theories in the limit of small 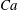$Ca$. The governing equations are obtained from the Poisson and dissipation brackets, as developed for an incompressible fluid system endowed with an internal contravariant second-order tensor, subject to the imposition of the constraint of a unit determinant. First proposed by Maffettone & Minale (J. Non-Newtonian Fluid Mech., vol. 78, 1998, pp. 227–241), this constraint physically corresponds to conservation of the volume of the dispersed phase in the emulsion. The Hamiltonian of the emulsion is expressed through the surface energy of the dispersed phase, in addition to the kinetic energy, following previous work by Grmela et al. (J. Non-Newtonian Fluid Mech., vol. 212, 2014, pp. 1–12), but employing a more accurate evaluation of the surface area in terms of the internal contravariant conformation tensor. Structural predictions of the ellipsoid droplet morphology obtained with the new model are compared with classic experiments by Torza et al. (J. Colloid Interface Sci., vol. 38, 1972, pp. 395–411), showing good agreement.

JFM classification

Complex Fluids: Emulsions Mathematical Foundations: Hamiltonian theory Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 433 - 473
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ait-Kadi, A., Ramazani, A., Grmela, M. & Zhou, C. 1999 ‘Volume preserving’ rheological models for polymer melts and solutions using the GENERIC formalism. J. Rheol. 43, 51–72.Google Scholar
Almusallam, A. S., Larson, R. G. & Solomon, M. J. 2000 A constitutive model for the prediction of ellipsoidal droplet shapes and stresses in immiscible blends. J. Rheol. 44, 1055–1083.CrossRefGoogle Scholar
Almusallam, A. S., Larson, R. G. & Solomon, M. J. 2004 Comprehensive constitutive model for immiscible blends of Newtonian polymers. J. Rheol. 48, 319–348.Google Scholar
Barthes-Bièsel, D. & Acrivos, A. 1973 Deformation and burst of a liquid droplet freely suspended in a linear shear field. J. Fluid Mech. 61, 1–22.CrossRefGoogle Scholar
Batchelor, G. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.Google Scholar
Bentley, B. J. & Leal, L. G. 1986 An experimental investigation of drop deformation and breakup in steady, two-dimensional linear flows. J. Fluid Mech. 167, 241–283.CrossRefGoogle Scholar
Beris, A. N. & Edwards, B. J. 1994 Thermodynamics of Flowing Systems with Internal Microstructure. Oxford University Press.CrossRefGoogle Scholar
Beyer, W. H. 1987 CRC Standard Mathematical Tables, 28th edn. CRC Press.Google Scholar
Chaffey, C. E. & Brenner, H. 1967 A second-order theory for shear deformation of drops. J. Colloid Interface Sci. 24, 258–269.Google Scholar
Choi, S. J. & Schowalter, W. R. 1972 Rheological properties of nondilute suspensions of deformable particles. Phys. Fluids 18, 420–427.Google Scholar
Delaby, I., Muller, R. & Ernst, B. 1995 Drop deformation during elongational flow in blends of viscoelastic fluids. Small deformation theory and comparison with experimental results. Rheol. Acta 34, 525–533.Google Scholar
Doi, M. & Ohta, T. 1991 Dynamics and rheology of complex interfaces. I. J. Chem. Phys. 95, 1242–1248.Google Scholar
Edwards, B. J. 1998 An analysis of single and double generator thermodynamic formalisms for the macroscopic description of complex fluids. J. Non-Equilib. Thermodyn. 23, 301–333.Google Scholar
Edwards, B. J., Beris, A. N. & Öttinger, H. C. 1998 An analysis of single and double generator thermodynamic formalisms for complex fluids. II. The microscopic description. J. Non-Equilib. Thermodyn. 23, 334–350.Google Scholar
Edwards, B. J. & Dressler, M. 2003 A rheological model with constant approximate volume for immiscible blends of ellipsoidal droplets. Rheol. Acta 42, 326–337.Google Scholar
Edwards, B. J., Dressler, M., Grmela, M. & Ait-Kadi, A. 2003 Rheological models with microstructural constraints. Rheol. Acta 42, 64–72.Google Scholar
Einstein, A. 1906 A new determination of molecular dimensions. Ann. Phys. 19, 289–306.Google Scholar
Einstein, A. 1911 Ann. Phys. 34, 591 (errata).Google Scholar
Frankel, N. A. & Acrivos, A. 1970 The constitutive equation for a dilute emulsion. J. Fluid Mech. 44, 65–78.Google Scholar
Gordon, R. J. & Schowalter, W. R. 1972 Anisotropic fluid theory: a different approach to the dumbbell theory of dilute polymer solutions. Trans. Soc. Rheol. 16, 79–97.Google Scholar
Grmela, M. 1984 Particle and bracket formulations of kinetic equations. Contemp. Maths 28, 125–132.Google Scholar
Grmela, M. 1991 Mesoscopic dynamics and thermodynamics: applications to polymeric fluids. In Rheological Modelling: Thermodynamical and Statistical Approaches (ed. Casas-Vazquez, J. & Jou, D.), Lecture Notes in Physics, vol. 381, pp. 99–125. Springer.Google Scholar
Grmela, M. 1993 Thermodynamics of driven systems. Phys. Rev. E 48, 919–930.Google Scholar
Grmela, M. & Ait-Kadi, A. 1998 Rheology of inhomogeneous immiscible blends. J. Non-Newtonian Fluid Mech. 77, 191–199.Google Scholar
Grmela, M., Ait-Kadi, A. & Utracki, L. A. 1998 Blends of two immiscible and rheologically different fluids. J. Non-Newtonian Fluid Mech. 77, 253–259.CrossRefGoogle Scholar
Grmela, M., Ammar, A., Chinesta, F. & Maîtrejean, G. 2014 A mesoscopic rheological model of moderately concentrated colloids. J. Non-Newtonian Fluid Mech. 212, 1–12.Google Scholar
Grmela, M., Bousmina, M. & Palierne, J. M. 2001 On the rheology of immiscible blends. Rheol. Acta 40, 560–569.Google Scholar
Grmela, M. & Öttinger, H. C. 1997 Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 56, 6620–6632.Google Scholar
Guenther, G. K. & Baird, D. G. 1996 An evaluation of the Doi–Ohta theory for an immiscible polymer blend. J. Rheol. 40, 1–20.Google Scholar
Guido, S. & Villone, M. 1998 Three-dimensional shape of a drop under simple shear flow. J. Rheol. 42, 395–415.Google Scholar
Hager, W. W. 1989 Updating the inverse of a matrix. SIAM Rev. 31 (2), 221–239.Google Scholar
Hand, G. L. 1962 A theory of anisotropic fluids. J. Fluid Mech. 13, 33–46.Google Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, vol. 1. Springer.Google Scholar
Jackson, N. E. & Tucker, C. L. III 2003 A model for large deformation of an ellipsoidal droplet with interfacial tension. J. Rheol. 47, 659–682.Google Scholar
Jaumann, G. 1911 Geschlossenes System physikalischer und chemischer Differentialgesetze. Sitz.ber Akad. Wiss. Wien IIa 120, 385–530.Google Scholar
Keller, S. R. 1979 On the surface area of the ellipsoid. Maths Comput. 33, 310–314.Google Scholar
Kennedy, M. R., Pozrikidis, C. & Skalak, R. 1994 Motion and deformation of liquid drops, and the rheology of dilute emulsions in simple shear flow. Comput. Fluids 23, 251–278.Google Scholar
Lee, H. M. & Park, O. O. 1994 Rheology and dynamics of immiscible polymer blends. J. Rheol. 38, 1405–1425.Google Scholar
Loewenberg, M. & Hinch, E. J. 1996 Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech. 321, 395–419.Google Scholar
Maffettone, P. & Minale, M. 1998 Equation of change for ellipsoidal drops in viscous flow. J. Non-Newtonian Fluid Mech. 78, 227–241.Google Scholar
Minale, M. 2004 Deformation of a non-Newtonian ellipsoidal drop in a non-Newtonian matrix: extension of Maffettone–Minale model. J. Non-Newtonian Fluid Mech. 123, 151–160.CrossRefGoogle Scholar
Minale, M. 2010 Models for the deformation of a single ellipsoidal drop: a review. Rheol. Acta 49, 789–806.Google Scholar
Mwasame, P. M., Wagner, N. J. & Beris, A. N. 2017 On the macroscopic modeling of dilute emulsions under flow in the presence of particle inertia. Phys. Fluids (submitted).Google Scholar
Oldroyd, J. G. 1953 The elastic and viscous properties of emulsions and suspensions. Proc. R. Soc. Lond. A 218, 122–132.Google Scholar
Öttinger, H. C. & Grmela, M. 1997 Dynamics and thermodynamics of complex fluids. II. Illustrations of a general formalism. Phys. Rev. E 56, 6633–6655.Google Scholar
Palierne, J. F. 1990 Linear rheology of viscoelastic emulsions with interfacial tension. Rheol. Acta 29, 204–214.Google Scholar
Raja, R. V., Subramanian, G. & Koch, D. L. 2010 Inertial effects on the rheology of a dilute emulsion. J. Fluid Mech. 646, 255–296.Google Scholar
Rallison, J. M. 1980 Note on the time-dependent deformation of a viscous drop which is almost spherical. J. Fluid Mech. 98, 625–633.Google Scholar
Rallison, J. M. 1984 The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 16, 45–66.Google Scholar
Rallison, J. M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89, 191–200.Google Scholar
Schowalter, W. R., Chaffey, C. E. & Brenner, H. 1968 Rheological behavior of a dilute emulsion. J. Colloid Interface Sci. 26, 152–160.Google Scholar
Stone, H. W. 1994 Dynamics of drop deformation and breakup in viscous fluids. The viscosity of a fluid containing small drops of another fluid. Annu. Rev. Fluid Mech. 26, 65–102.CrossRefGoogle Scholar
Takahashi, Y., Kurashima, N., Noda, I. & Doi, M. 1994 Experimental tests of the scaling relation for textured materials in mixtures of two immiscible fluids. J. Rheol. 38, 699–712.Google Scholar
Taylor, G. I. 1932 The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. A 138, 41–48.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146, 501–523.Google Scholar
Torza, S., Cox, R. & Mason, S. G. 1972 Particle motions in sheared suspensions XXVII. Transient and steady deformation and burst of liquid drops. J. Colloid Interface Sci. 38, 395–411.Google Scholar
Vermant, J., Van Puyvelde, P., Moldenaers, P., Mewis, J. & Fuller, G. G. 1998 Anisotropy and orientation of the microstructure in viscous emulsions during shear flow. Langmuir 14, 1612–1617.Google Scholar
Wagner, N. J., Öttinger, H. C. & Edwards, B. J. 1999 Generalized Doi–Ohta model for multiphase flow developed via GENERIC. AIChE J. 45, 1169–1181.Google Scholar
Vinckier, I., Mewis, J. & Moldenaers, P. 1997 Stress relaxation as a microstructural probe for immiscible polymer blends. Rheol. Acta 36, 513–523.Google Scholar
Vinckier, I., Moldenaers, P. & Mewis, J. 1996 Relationship between rheology and morphology of model blends in steady shear flow. J. Rheol. 40, 613–631.Google Scholar
Wetzel, E. D. & Tucker, C. L. III 1999 Area tensors for modeling microstructure during laminar liquid–liquid mixing. Intl J. Multiphase Flow 25, 35–61.Google Scholar
Wetzel, E. D. & Tucker, C. L. III 2001 Droplet deformation in dispersions with unequal viscosities and zero interfacial tension. J. Fluid Mech. 426, 199–228.Google Scholar
Xu, D., Cui, J., Bansal, R., Hao, X., Liu, J., Chen, W. & Peterson, B. S. 2009 The ellipsoidal area ratio: an alternative anisotropy index for diffusion tensor imaging. J. Magn. Reson. Imag. 27 (3), 311–323.Google Scholar
Yu, W. & Bousima, M. 2003 Ellipsoidal model for droplet deformation in emulsions. J. Rheol. 47, 1011–1039.Google Scholar
Yu, W. & Zhou, C. 2007 A simple constitutive equation for immiscible blends. J. Rheol. 51, 179–194.Google Scholar