Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Danaila, Ionut
and
Protas, Bartosz
2015.
Optimal reconstruction of inviscid vortices.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 471,
Issue. 2180,
p.
20150323.
Lorenzi, Stefano
Cammi, Antonio
Luzzi, Lelio
and
Rozza, Gianluigi
2016.
POD-Galerkin method for finite volume approximation of Navier–Stokes and RANS equations.
Computer Methods in Applied Mechanics and Engineering,
Vol. 311,
Issue. ,
p.
151.
Tammisola, O.
and
Juniper, M. P.
2016.
Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
620.
Lasagna, Davide
Huang, Deqing
Tutty, Owen R.
and
Chernyshenko, Sergei
2016.
Sum-of-squares approach to feedback control of laminar wake flows.
Journal of Fluid Mechanics,
Vol. 809,
Issue. ,
p.
628.
Podvin, Bérengère
and
Sergent, Anne
2017.
Precursor for wind reversal in a square Rayleigh-Bénard cell.
Physical Review E,
Vol. 95,
Issue. 1,
Pyta, L.
and
Abel, D.
2017.
Online Model Adaption of Reduced Order Models for Fluid Flows * *The authors gratefully acknowledge funding from the German Research Foundation (DFG) for the Research Unit ‘Active Drag Reduction’ (AB65/12-1).
IFAC-PapersOnLine,
Vol. 50,
Issue. 1,
p.
11138.
Pyta, Lorenz
Meysonnat, Pascal S.
Schroder, Wolfgang
and
Abel, Dirk
2017.
Space-selective nonlinear reduced-order models for turbulent boundary layer drag reduction.
p.
383.
Schiavo, Luiz A. C. A.
Wolf, William Roberto
and
Azevedo, João Luiz F.
2017.
Turbulent kinetic energy budgets in wall bounded flows with pressure gradients and separation.
Physics of Fluids,
Vol. 29,
Issue. 11,
Lorenzi, Stefano
Cammi, Antonio
Luzzi, Lelio
and
Rozza, Gianluigi
2017.
A reduced order model for investigating the dynamics of the Gen-IV LFR coolant pool.
Applied Mathematical Modelling,
Vol. 46,
Issue. ,
p.
263.
Schiavo, Luiz Augusto C.
Azevedo, Joao Luiz F.
and
Wolf, William
2017.
Investigation of Turbulence Properties in Wall-Bounded Flows with Pressure Gradients and Separation.
Wells, D.
Wang, Z.
Xie, X.
and
Iliescu, T.
2017.
An evolve‐then‐filter regularized reduced order model for convection‐dominated flows.
International Journal for Numerical Methods in Fluids,
Vol. 84,
Issue. 10,
p.
598.
Xie, Xuping
Wells, David
Wang, Zhu
and
Iliescu, Traian
2017.
Approximate deconvolution reduced order modeling.
Computer Methods in Applied Mechanics and Engineering,
Vol. 313,
Issue. ,
p.
512.
Resseguier, Valentin
Mémin, Etienne
Heitz, Dominique
and
Chapron, Bertrand
2017.
Stochastic modelling and diffusion modes for proper orthogonal decomposition models and small-scale flow analysis.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
888.
Dupuis, Romain
Jouhaud, Jean-Christophe
and
Sagaut, Pierre
2018.
Aerodynamic Data Predictions for Transonic Flows via a Machine-Learning-based Surrogate Model.
Xie, X.
Mohebujjaman, M.
Rebholz, L. G.
and
Iliescu, T.
2018.
Data-Driven Filtered Reduced Order Modeling of Fluid Flows.
SIAM Journal on Scientific Computing,
Vol. 40,
Issue. 3,
p.
B834.
Dupuis, Romain
Jouhaud, Jean-Christophe
and
Sagaut, Pierre
2018.
Surrogate Modeling of Aerodynamic Simulations for Multiple Operating Conditions Using Machine Learning.
AIAA Journal,
Vol. 56,
Issue. 9,
p.
3622.
Rahman, Sk. M.
Ahmed, S. E.
and
San, O.
2019.
A dynamic closure modeling framework for model order reduction of geophysical flows.
Physics of Fluids,
Vol. 31,
Issue. 4,
Zerfas, Camille
Rebholz, Leo G.
Schneier, Michael
and
Iliescu, Traian
2019.
Continuous data assimilation reduced order models of fluid flow.
Computer Methods in Applied Mechanics and Engineering,
Vol. 357,
Issue. ,
p.
112596.
Lui, Hugo F. S.
and
Wolf, William R.
2019.
Construction of reduced-order models for fluid flows using deep feedforward neural networks.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
963.
Xie, Xuping
Zhang, Guannan
and
Webster, Clayton G.
2019.
Non-Intrusive Inference Reduced Order Model for Fluids Using Deep Multistep Neural Network.
Mathematics,
Vol. 7,
Issue. 8,
p.
757.
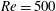 $\mathit{Re}=500$
(based on the initial vorticity thickness and the velocity of the high-speed stream) and a 3D Ahmed body wake at
$\mathit{Re}=500$
(based on the initial vorticity thickness and the velocity of the high-speed stream) and a 3D Ahmed body wake at
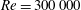 $\mathit{Re}=300\,000$
(based on the body height and the free-stream velocity). The variational optimization formulation elucidates a number of interesting physical insights concerning the eddy-viscosity ansatz used. The 20-dimensional model of the mixing-layer reveals a negative eddy-viscosity regime at low fluctuation levels which improves the transient times towards the attractor. The 100-dimensional wake model yields more accurate energy distributions as compared to the nonlinear modal eddy-viscosity benchmark proposed recently by Östh et al. (J. Fluid Mech., vol. 747, 2014, pp. 518–544). Our methodology can be applied to construct quite arbitrary closure relations and, more generally, constitutive relations optimizing statistical properties of a broad class of reduced-order models.
$\mathit{Re}=300\,000$
(based on the body height and the free-stream velocity). The variational optimization formulation elucidates a number of interesting physical insights concerning the eddy-viscosity ansatz used. The 20-dimensional model of the mixing-layer reveals a negative eddy-viscosity regime at low fluctuation levels which improves the transient times towards the attractor. The 100-dimensional wake model yields more accurate energy distributions as compared to the nonlinear modal eddy-viscosity benchmark proposed recently by Östh et al. (J. Fluid Mech., vol. 747, 2014, pp. 518–544). Our methodology can be applied to construct quite arbitrary closure relations and, more generally, constitutive relations optimizing statistical properties of a broad class of reduced-order models.


