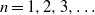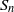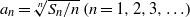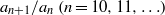Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Yi
and
Zhu, BaoXuan
2014.
Proofs of some conjectures on monotonicity of number-theoretic and combinatorial sequences.
Science China Mathematics,
Vol. 57,
Issue. 11,
p.
2429.
DeSalvo, Stephen
and
Pak, Igor
2015.
Log-concavity of the partition function.
The Ramanujan Journal,
Vol. 38,
Issue. 1,
p.
61.
Chen, William Y. C.
and
Zheng, Ken Y.
2017.
The log-behavior of
$$\root n \of {p(n)}$$
p
(
n
)
n
and
$$\root n \of {p(n)/n}$$
p
(
n
)
/
n
n
.
The Ramanujan Journal,
Vol. 44,
Issue. 2,
p.
281.
Mansour, Toufik
and
Shattuck, Mark
2017.
A monotonicity property for generalized Fibonacci sequences.
Mathematica Slovaca,
Vol. 67,
Issue. 3,
p.
585.
Hou, Qing-Hu
and
Zhang, Zuo-Ru
2019.
r-log-concavity of partition functions.
The Ramanujan Journal,
Vol. 48,
Issue. 1,
p.
117.
Kosyak, Alexandre
Moree, Pieter
Sofos, Efthymios
and
Zhang, Bin
2021.
CYCLOTOMIC POLYNOMIALS WITH PRESCRIBED HEIGHT AND PRIME NUMBER THEORY.
Mathematika,
Vol. 67,
Issue. 1,
p.
214.
Mukherjee, Gargi
2023.
Log-convexity and the overpartition function.
The Ramanujan Journal,
Vol. 60,
Issue. 2,
p.
517.
Gajdzica, Krystian
2023.
Log-concavity of the restricted partition function pA(n,k) and the new Bessenrodt-Ono type inequality.
Journal of Number Theory,
Vol. 251,
Issue. ,
p.
31.