39 results
Swimming with swirl in a viscoelastic fluid
-
- Journal:
- Journal of Fluid Mechanics / Volume 900 / 10 October 2020
- Published online by Cambridge University Press:
- 31 July 2020, A4
-
- Article
- Export citation
Oscillatory spontaneous dimpling in evaporating curved thin films
-
- Journal:
- Journal of Fluid Mechanics / Volume 889 / 25 April 2020
- Published online by Cambridge University Press:
- 24 February 2020, A25
-
- Article
- Export citation
Pressure-driven flow of a vesicle through a square microchannel
-
- Journal:
- Journal of Fluid Mechanics / Volume 861 / 25 February 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 447-483
-
- Article
- Export citation
Stokes flow of vesicles in a circular tube
-
- Journal:
- Journal of Fluid Mechanics / Volume 851 / 25 September 2018
- Published online by Cambridge University Press:
- 30 July 2018, pp. 606-635
-
- Article
- Export citation
Suspension flow through an asymmetric T-junction
-
- Journal:
- Journal of Fluid Mechanics / Volume 844 / 10 June 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 247-273
-
- Article
- Export citation
The steady motion of a closely fitting vesicle in a tube
-
- Journal:
- Journal of Fluid Mechanics / Volume 835 / 25 January 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 721-761
-
- Article
- Export citation
Heat/mass transport in shear flow over a reactive surface with inert defects
-
- Journal:
- Journal of Fluid Mechanics / Volume 811 / 25 January 2017
- Published online by Cambridge University Press:
- 13 December 2016, pp. 372-399
-
- Article
- Export citation
Heat/mass transport in shear flow over a heterogeneous surface with first-order surface-reactive domains
-
- Journal:
- Journal of Fluid Mechanics / Volume 782 / 10 November 2015
- Published online by Cambridge University Press:
- 08 October 2015, pp. 260-299
-
- Article
- Export citation
Pearling, wrinkling, and buckling of vesicles in elongational flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 777 / 25 August 2015
- Published online by Cambridge University Press:
- 15 July 2015, pp. 1-26
-
- Article
- Export citation
Nonlinear instability of a supersonic boundary layer with two-dimensional roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 752 / 10 August 2014
- Published online by Cambridge University Press:
- 09 July 2014, pp. 497-520
-
- Article
- Export citation
The mechanism of shape instability for a vesicle in extensional flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 750 / 10 July 2014
- Published online by Cambridge University Press:
- 02 June 2014, pp. 144-190
-
- Article
- Export citation
The dynamics of a non-dilute vesicle suspension in a simple shear flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 725 / 25 June 2013
- Published online by Cambridge University Press:
- 23 May 2013, pp. 709-731
-
- Article
- Export citation
The shape stability of a lipid vesicle in a uniaxial extensional flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 719 / 25 March 2013
- Published online by Cambridge University Press:
- 19 February 2013, pp. 345-361
-
- Article
- Export citation
Flow of power-law fluids in fixed beds of cylinders or spheres
-
- Journal:
- Journal of Fluid Mechanics / Volume 713 / 25 December 2012
- Published online by Cambridge University Press:
- 29 October 2012, pp. 491-527
-
- Article
- Export citation
Effects of viscoelasticity in the high Reynolds number cylinder wake
-
- Journal:
- Journal of Fluid Mechanics / Volume 693 / 25 February 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 297-318
-
- Article
- Export citation
The dynamics of a vesicle in simple shear flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 674 / 10 May 2011
- Published online by Cambridge University Press:
- 23 March 2011, pp. 578-604
-
- Article
- Export citation
Disturbance evolution in a Mach 4.8 boundary layer with two-dimensional roughness-induced separation and shock
-
- Journal:
- Journal of Fluid Mechanics / Volume 648 / 10 April 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 435-469
-
- Article
- Export citation
Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate Reynolds numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 651 / 25 May 2010
- Published online by Cambridge University Press:
- 29 March 2010, pp. 415-442
-
- Article
- Export citation
The effect of Brownian motion on the stability of sedimenting suspensions of polarizable rods in an electric field
-
- Journal:
- Journal of Fluid Mechanics / Volume 624 / 10 April 2009
- Published online by Cambridge University Press:
- 10 April 2009, pp. 361-388
-
- Article
- Export citation
Direct numerical simulation of polymer-induced drag reduction in turbulent boundary layer flow of inhomogeneous polymer solutions
-
- Journal:
- Journal of Fluid Mechanics / Volume 566 / 10 November 2006
- Published online by Cambridge University Press:
- 05 October 2006, pp. 153-162
-
- Article
- Export citation



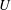
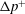
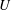
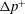
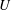
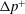

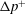

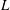
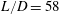

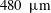

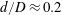

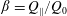
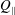
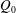
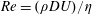

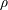
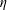
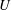
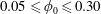
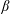
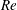
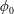
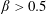
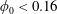
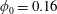

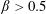
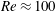
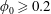



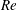

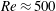
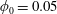

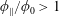
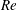
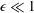

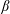
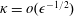
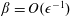

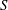
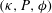
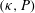
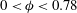
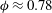
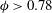
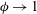
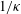
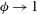
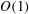
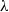
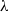
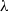



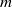

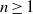
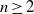
 , Newtonian flow past a circular cylinder exhibits a wake and detached shear layers which have transitioned to turbulence. It is the goal of the present study to investigate the effects which viscoelasticity has on this state and to identify the mechanisms responsible for wake stabilization. It is found through numerical simulations (employing the FENE-P rheological model) that viscoelasticity greatly reduces the amount of turbulence in the wake, reverting it back to a state which qualitatively appears similar to the Newtonian mode B instability which occurs at lower
, Newtonian flow past a circular cylinder exhibits a wake and detached shear layers which have transitioned to turbulence. It is the goal of the present study to investigate the effects which viscoelasticity has on this state and to identify the mechanisms responsible for wake stabilization. It is found through numerical simulations (employing the FENE-P rheological model) that viscoelasticity greatly reduces the amount of turbulence in the wake, reverting it back to a state which qualitatively appears similar to the Newtonian mode B instability which occurs at lower 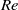 . By focusing on the separated shear layers, it is found that viscoelasticity suppresses the formation of the Kelvin–Helmholtz instability which dominates for Newtonian flows, consistent with previous studies of viscoelastic free shear layers. Through this shear layer stabilization, the viscoelastic far wake is then subject to the same instability mechanisms which dominate for Newtonian flows, but at far lower Reynolds numbers.
. By focusing on the separated shear layers, it is found that viscoelasticity suppresses the formation of the Kelvin–Helmholtz instability which dominates for Newtonian flows, consistent with previous studies of viscoelastic free shear layers. Through this shear layer stabilization, the viscoelastic far wake is then subject to the same instability mechanisms which dominate for Newtonian flows, but at far lower Reynolds numbers.