The fundamental question in reverse mathematics is to determine which set existence axioms are required to prove particular theorems of mathematics. In addition to being interesting in their own right, answers to this question have consequences in both effective mathematics and the foundations of mathematics. Before discussing these consequences, we need to be more specific about the motivating question.
Reverse mathematics is useful for studying theorems of either countable or essentially countable mathematics. Essentially countable mathematics is a vague term that is best explained by an example. Complete separable metric spaces are essentially countable because, although the spaces may be uncountable, they can be understood in terms of a countable basis. Simpson (1985) gives the following list of areas which can be analyzed by reverse mathematics: number theory, geometry, calculus, differential equations, real and complex analysis, combinatorics, countable algebra, separable Banach spaces, computability theory, and the topology of complete separable metric spaces. Reverse mathematics is less suited to theorems of abstract functional analysis, abstract set theory, universal algebra, or general topology.
Section 2 introduces the major subsystems of second order arithmetic used in reverse mathematics: RCA0, WKL0, ACA0, ATR0 and 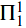 – CA0. Sections 3 through 7 consider various theorems of ordered group theory from the perspective of reverse mathematics. Among the results considered are theorems on ordered quotient groups (including an equivalent of ACA0), groups and semigroup conditions which imply orderability (WKL0), the orderability of free groups (RCA0), Hölder's Theorem (RCA0), Mal'tsev's classification of the order types of countable ordered groups (
– CA0. Sections 3 through 7 consider various theorems of ordered group theory from the perspective of reverse mathematics. Among the results considered are theorems on ordered quotient groups (including an equivalent of ACA0), groups and semigroup conditions which imply orderability (WKL0), the orderability of free groups (RCA0), Hölder's Theorem (RCA0), Mal'tsev's classification of the order types of countable ordered groups (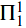 – CA0)
– CA0)
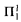 – CA0 and order types of countable ordered groups
– CA0 and order types of countable ordered groups



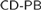
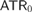
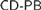
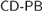
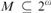
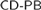
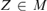
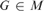
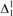
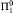 chains and antichains, in infinite computable stable and weakly stable posets. For example, we extend a result of Hirschfeldt and Shore to show that every infinite computable weakly stable poset contains either an infinite low chain or an infinite computable antichain. Our hardest result is that there is an infinite computable weakly stable poset with no infinite
chains and antichains, in infinite computable stable and weakly stable posets. For example, we extend a result of Hirschfeldt and Shore to show that every infinite computable weakly stable poset contains either an infinite low chain or an infinite computable antichain. Our hardest result is that there is an infinite computable weakly stable poset with no infinite 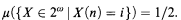
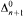 -condition. We show that all trees which are not computably categorical have computable dimension ω. Finally, we prove that for every
-condition. We show that all trees which are not computably categorical have computable dimension ω. Finally, we prove that for every 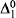 formulas and adding a formula induction scheme for
formulas and adding a formula induction scheme for 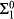 formulas. For the purposes of this paper, we will be concerned with fairly weak extensions of RCA
formulas. For the purposes of this paper, we will be concerned with fairly weak extensions of RCA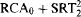 must contain a nonlow set.
must contain a nonlow set.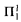 –
– 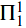 –
– 