Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Calvert, Wesley
Cenzer, Douglas
Harizanov, Valentina
and
Morozov, Andrei
2006.
Effective categoricity of equivalence structures.
Annals of Pure and Applied Logic,
Vol. 141,
Issue. 1-2,
p.
61.
Csima, Barbara F.
Khoussainov, Bakhadyr
and
Liu, Jiamou
2008.
Logic and Theory of Algorithms.
Vol. 5028,
Issue. ,
p.
139.
Binns, Stephen
Kjos-Hanssen, Bjørn
Lerman, Manuel
Schmerl, James H.
and
Solomon, Reed
2008.
Self-Embeddings of Computable Trees.
Notre Dame Journal of Formal Logic,
Vol. 49,
Issue. 1,
Calvert, Wesley
Cenzer, Douglas
Harizanov, Valentina S.
and
Morozov, Andrei
2009.
Effective categoricity of Abelian p-groups.
Annals of Pure and Applied Logic,
Vol. 159,
Issue. 1-2,
p.
187.
Melnikov, Alexander G.
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
362.
Melnikov, Alexander G.
2010.
Programs, Proofs, Processes.
Vol. 6158,
Issue. ,
p.
321.
Cenzer, D.
Harizanov, V.
and
Remmel, J. B.
2013.
Two-to-one structures.
Journal of Logic and Computation,
Vol. 23,
Issue. 6,
p.
1195.
Dushenin, D. I.
2013.
Abelian p-groups and autostability relative to an oracle.
Algebra and Logic,
Vol. 52,
Issue. 4,
p.
269.
Miller, Russell
and
Shlapentokh, Alexandra
2014.
Computable categoricity for algebraic fields with splitting algorithms.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 6,
p.
3955.
Miller, Russell
Solomon, Reed
and
Steiner, Rebecca M.
2014.
Language, Life, Limits.
Vol. 8493,
Issue. ,
p.
314.
Dushenin, D. I.
2014.
Arithmetical Isomorphisms of Abelian p-Groups.
Journal of Mathematical Sciences,
Vol. 203,
Issue. 4,
p.
455.
Hirschfeldt, Denis
Kramer, Ken
Miller, Russell
and
Shlapentokh, Alexandra
2014.
Categoricity properties for computable algebraic fields.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 6,
p.
3981.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Downey, Rodney G.
Kach, Asher M.
Lempp, Steffen
Lewis-Pye, Andrew E.M.
Montalbán, Antonio
and
Turetsky, Daniel D.
2015.
The complexity of computable categoricity.
Advances in Mathematics,
Vol. 268,
Issue. ,
p.
423.
Harris, Charles M.
2015.
On limitwise monotonicity and maximal block functions.
Computability,
Vol. 4,
Issue. 2,
p.
119.
Levin, Oscar
2016.
Computable dimension for ordered fields.
Archive for Mathematical Logic,
Vol. 55,
Issue. 3-4,
p.
519.
Adams, Francis
and
Cenzer, Douglas
2017.
Computability and categoricity of weakly ultrahomogeneous structures.
Computability,
Vol. 6,
Issue. 4,
p.
365.
Hirschfeldt, Denis R.
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
22.
Walker, Hakim J.
2018.
Computable isomorphisms for certain classes of infinite graphs.
Journal of Knot Theory and Its Ramifications,
Vol. 27,
Issue. 07,
p.
1841012.
Mahmoud, Mohammad Assem
2019.
Degrees of categoricity of trees and the isomorphism problem.
Mathematical Logic Quarterly,
Vol. 65,
Issue. 3,
p.
293.

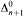 -condition. We show that all trees which are not computably categorical have computable dimension ω. Finally, we prove that for every
-condition. We show that all trees which are not computably categorical have computable dimension ω. Finally, we prove that for every 