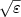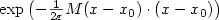In this paper, we study the homogenization and localization of a spectral transport equation posed in a locally periodic heterogeneous domain. This equation models the equilibrium of particles interacting with an underlying medium in the presence of a creation mechanism such as, for instance, neutrons in nuclear reactors. The physical coefficients of the domain are ε-periodic functions modulated by a macroscopic variable, where ε is a small parameter. The mean free path of the particles is also of order ε. We assume that the leading eigenvalue of the periodicity cell problem admits a unique minimum in the domain at a point x 0 where its Hessian matrix is positive definite. This assumption yields a concentration phenomenon around x 0, as ε goes to 0, at a new scale of the order of $\sqrt{\varepsilon}$ 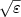 which is superimposed with the usual ε oscillations of the homogenized limit. More precisely, we prove that the particle density is asymptotically the product of two terms. The first one is the leading eigenvector of a cell transport equation with periodic boundary conditions. The second term is the first eigenvector of a homogenized diffusion equation in the whole space with quadratic potential, rescaled by a factor $\sqrt{\varepsilon}$
which is superimposed with the usual ε oscillations of the homogenized limit. More precisely, we prove that the particle density is asymptotically the product of two terms. The first one is the leading eigenvector of a cell transport equation with periodic boundary conditions. The second term is the first eigenvector of a homogenized diffusion equation in the whole space with quadratic potential, rescaled by a factor $\sqrt{\varepsilon}$ 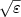 , i.e., of the form $\exp \left (- \frac {1} {2 \varepsilon} M (x-x_0)\cdot (x-x_0) \right )$
, i.e., of the form $\exp \left (- \frac {1} {2 \varepsilon} M (x-x_0)\cdot (x-x_0) \right )$ 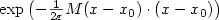 , where M is a positive definite matrix. Furthermore, the eigenvalue corresponding to this second term gives a first-order correction to the eigenvalue of the heterogeneous spectral transport problem.
, where M is a positive definite matrix. Furthermore, the eigenvalue corresponding to this second term gives a first-order correction to the eigenvalue of the heterogeneous spectral transport problem.