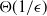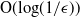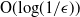Motivated by applications to wireless networks, cloud computing, data centers, etc., stochastic processing networks have been studied in the literature under various asymptotic regimes. In the heavy traffic regime, the steady-state mean queue length is proved to be 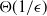 $\Theta({1}/{\epsilon})$
, where
$\Theta({1}/{\epsilon})$
, where  $\epsilon$
is the heavy traffic parameter (which goes to zero in the limit). The focus of this paper is on obtaining queue length bounds on pre-limit systems, thus establishing the rate of convergence to heavy traffic. For the generalized switch, operating under the MaxWeight algorithm, we show that the mean queue length is within
$\epsilon$
is the heavy traffic parameter (which goes to zero in the limit). The focus of this paper is on obtaining queue length bounds on pre-limit systems, thus establishing the rate of convergence to heavy traffic. For the generalized switch, operating under the MaxWeight algorithm, we show that the mean queue length is within 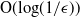 $\textrm{O}({\log}({1}/{\epsilon}))$
of its heavy traffic limit. This result holds regardless of the complete resource pooling (CRP) condition being satisfied. Furthermore, when the CRP condition is satisfied, we show that the mean queue length under the MaxWeight algorithm is within
$\textrm{O}({\log}({1}/{\epsilon}))$
of its heavy traffic limit. This result holds regardless of the complete resource pooling (CRP) condition being satisfied. Furthermore, when the CRP condition is satisfied, we show that the mean queue length under the MaxWeight algorithm is within 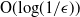 $\textrm{O}({\log}({1}/{\epsilon}))$
of the optimal scheduling policy. Finally, we obtain similar results for the rate of convergence to heavy traffic of the total queue length in load balancing systems operating under the ‘join the shortest queue’ routeing algorithm.
$\textrm{O}({\log}({1}/{\epsilon}))$
of the optimal scheduling policy. Finally, we obtain similar results for the rate of convergence to heavy traffic of the total queue length in load balancing systems operating under the ‘join the shortest queue’ routeing algorithm.