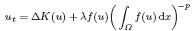The conditions under which the solution of the non-local thermistor problem
\begin{gather*} u_t=\Delta u+\frac{\lambda f(u)}{(\int_{\varOmega}f(u)\,\mathrm{d}x)^{2}},\quad x\in\varOmega\subset\mathbb{R}^N,\ N\geq2,\ t>0, \\ \frac{\partial u(x,t)}{\partial\nu}+\beta(x)u(x,t)=0,\quad x\in\partial\varOmega,\ t>0, \\ u(x,0)=u_0(x),\quad x\in\varOmega, \end{gather*}
blows up are investigated. We assume that $f(s)$ is a decreasing function and that it is integrable in $(0,\infty)$. Considering a suitable functional we prove that for all $\lambda\gt0$ the solution of the Neumann problem blows up in finite time. The same result is obtained for the Robin problem under the assumption that $\lambda$ is sufficiently large $(\lambda\gg 1)$. In the proof of existence of blow-up for the Dirichlet problem we use the subsolution technique. We are able to construct a blowing-up lower solution under the assumption that either $\lambda\gt\lambda^*$ or $0\lt\lambda\lt\lambda^*$, for some critical value $\lambda^*$, and that the initial condition is sufficiently large provided also that $f(s)$ satisfies the decay condition $\int_0^\infty[sf(s)-s^2f'(s)]\,\mathrm{d} s\lt\infty$.