Article contents
THE MAXIMUM SIZE OF 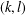 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
Published online by Cambridge University Press: 26 December 2018
Abstract
A subset 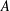 $A$ of a finite abelian group
$A$ of a finite abelian group 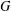 $G$ is called
$G$ is called 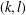 $(k,l)$-sum-free if the sum of
$(k,l)$-sum-free if the sum of 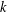 $k$ (not necessarily distinct) elements of
$k$ (not necessarily distinct) elements of 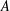 $A$ never equals the sum of
$A$ never equals the sum of 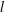 $l$ (not necessarily distinct) elements of
$l$ (not necessarily distinct) elements of 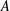 $A$. We find an explicit formula for the maximum size of a
$A$. We find an explicit formula for the maximum size of a 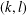 $(k,l)$-sum-free subset in
$(k,l)$-sum-free subset in 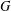 $G$ for all
$G$ for all 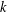 $k$ and
$k$ and 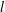 $l$ in the case when
$l$ in the case when 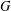 $G$ is cyclic by proving that it suffices to consider
$G$ is cyclic by proving that it suffices to consider 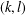 $(k,l)$-sum-free intervals in subgroups of
$(k,l)$-sum-free intervals in subgroups of  $G$. This simplifies and extends earlier results by Hamidoune and Plagne [‘A new critical pair theorem applied to sum-free sets in abelian groups’, Comment. Math. Helv. 79(1) (2004), 183–207] and Bajnok [‘On the maximum size of a
$G$. This simplifies and extends earlier results by Hamidoune and Plagne [‘A new critical pair theorem applied to sum-free sets in abelian groups’, Comment. Math. Helv. 79(1) (2004), 183–207] and Bajnok [‘On the maximum size of a 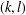 $(k,l)$-sum-free subset of an abelian group’, Int. J. Number Theory 5(6) (2009), 953–971].
$(k,l)$-sum-free subset of an abelian group’, Int. J. Number Theory 5(6) (2009), 953–971].
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by


