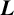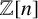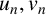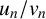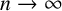Apéry’s famous proof [Reference van der Poorten10] of the irrationality of
![]() $\zeta (3)$
displayed a particular phenomenon (which could certainly have been dismissed if discussed only in the arithmetic context). One considers the recurrence equation
$\zeta (3)$
displayed a particular phenomenon (which could certainly have been dismissed if discussed only in the arithmetic context). One considers the recurrence equation
and its two rational solutions
![]() $u_n$
and
$u_n$
and
![]() $v_n$
, where
$v_n$
, where
![]() $n\ge 0$
, originating from the initial data
$n\ge 0$
, originating from the initial data
![]() $u_0=0$
,
$u_0=0$
,
![]() $u_1=6$
and
$u_1=6$
and
![]() $v_0=1$
,
$v_0=1$
,
![]() $v_1=5$
. Then
$v_1=5$
. Then
![]() $v_n$
are, in fact, integral for any
$v_n$
are, in fact, integral for any
![]() $n\ge 0$
and the denominators of
$n\ge 0$
and the denominators of
![]() $u_n$
have a moderate growth as
$u_n$
have a moderate growth as
![]() $n\to \infty $
, and are certainly not like
$n\to \infty $
, and are certainly not like
![]() $n!^3$
, as suggested by the recursion, but are
$n!^3$
, as suggested by the recursion, but are
![]() $O(C^n)$
for some
$O(C^n)$
for some
![]() $C>1$
. In fact,
$C>1$
. In fact,
![]() $D_n^3u_n\in \mathbb Z$
for all
$D_n^3u_n\in \mathbb Z$
for all
![]() $n\ge 1$
, where
$n\ge 1$
, where
![]() $D_n$
denotes the least common multiple of
$D_n$
denotes the least common multiple of
![]() $1,2,\dots ,n$
; the limit
$1,2,\dots ,n$
; the limit
![]() $D_n^{1/n}\to e$
as
$D_n^{1/n}\to e$
as
![]() $n\to \infty $
is a consequence of the prime number theorem. An important additional property is that the quotient
$n\to \infty $
is a consequence of the prime number theorem. An important additional property is that the quotient
![]() $u_n/v_n\to \zeta (3)$
as
$u_n/v_n\to \zeta (3)$
as
![]() $n\to \infty $
(and also
$n\to \infty $
(and also
![]() $u_n/v_n\ne \zeta (3)$
for all n). Even sharper,
$u_n/v_n\ne \zeta (3)$
for all n). Even sharper,
![]() $v_n\zeta (3)-u_n\to 0$
as
$v_n\zeta (3)-u_n\to 0$
as
![]() $n\to \infty $
, and, at the highest level of sharpness,
$n\to \infty $
, and, at the highest level of sharpness,
![]() $D_n^3(v_n\zeta (3)-u_n)\to 0$
as
$D_n^3(v_n\zeta (3)-u_n)\to 0$
as
![]() $n\to \infty $
. It is the latter sharpest form that leads to the conclusion
$n\to \infty $
. It is the latter sharpest form that leads to the conclusion
![]() $\zeta (3)\notin \mathbb Q$
. But already the arithmetic properties of
$\zeta (3)\notin \mathbb Q$
. But already the arithmetic properties of
![]() $u_n,v_n$
coupled with the ‘irrational’ limit relation
$u_n,v_n$
coupled with the ‘irrational’ limit relation
![]() $u_n/v_n\to \zeta (3)$
as
$u_n/v_n\to \zeta (3)$
as
![]() $n\to \infty $
are phenomenal.
$n\to \infty $
are phenomenal.
One way of proving all the above claims in one go is to recast the sequence
![]() $I_n=v_n\zeta (3)-u_n$
as the Beukers triple integral [Reference Beukers4]
$I_n=v_n\zeta (3)-u_n$
as the Beukers triple integral [Reference Beukers4]
 $$ \begin{align*} I_n=\frac12\int_0^1\!\int_0^1\!\int_0^1\frac{x^n(1-x)^ny^n(1-y)^nz^n(1-z)^n}{(1-(1-xy)z)^{n+1}}\,d x\,d y\,d z \quad\text{for } n=1,2,\ldots. \end{align*} $$
$$ \begin{align*} I_n=\frac12\int_0^1\!\int_0^1\!\int_0^1\frac{x^n(1-x)^ny^n(1-y)^nz^n(1-z)^n}{(1-(1-xy)z)^{n+1}}\,d x\,d y\,d z \quad\text{for } n=1,2,\ldots. \end{align*} $$
A routine use of creative telescoping machinery, based on the Almkvist–Zeilberger algorithm [Reference Almkvist and Zeilberger2] (in fact, its multivariable version [Reference Apagodu and Zeilberger3]), then shows that
![]() $I_n$
indeed satisfies (1), while the evaluations
$I_n$
indeed satisfies (1), while the evaluations
![]() $I_0=\zeta (3)$
and
$I_0=\zeta (3)$
and
![]() $I_1=5\zeta (3)-6$
are straightforward. The arithmetic and analytic properties follow from the analysis of the integrals
$I_1=5\zeta (3)-6$
are straightforward. The arithmetic and analytic properties follow from the analysis of the integrals
![]() $I_n$
performed in [Reference Beukers4]; more practically, they can be predicted and checked numerically based on the recurrence equation (1).
$I_n$
performed in [Reference Beukers4]; more practically, they can be predicted and checked numerically based on the recurrence equation (1).
A common belief is that we have a better understanding of the phenomenon these days. Namely, we possess some (highly nonsystematic!) recipes and strategies (see, for example, [Reference Almkvist, van Straten, Zudilin, Yui, Verrill and Doran1, Reference Chamberland and Straub6, Reference Dougherty-Bliss, Koutschan and Zeilberger7, Reference Zagier and Harnad13, Reference Zudilin15, Reference Zudilin16]) for getting other meaningful constants c as Apéry limits. In other words, there are (irreducible) recurrence equations with coefficients from
![]() $\mathbb Z[n]$
such that, for two rational solutions
$\mathbb Z[n]$
such that, for two rational solutions
![]() $u_n,v_n$
, we have
$u_n,v_n$
, we have
![]() $u_n/v_n\to c$
as
$u_n/v_n\to c$
as
![]() $n\to \infty $
and the denominators of
$n\to \infty $
and the denominators of
![]() $u_n,v_n$
are growing at most exponentially in n. (We may also consider weak Apéry limits when the latter condition on the growth of denominators is dropped.) Although one would definitely like to draw some conclusions about the irrationality of those constants c, this constraint for the arithmetic to be in the sharpest form would severely shorten the existing list of known Apéry limits; for example, it would throw out Catalan’s constant from the list. A very basic question is then as follows.
$u_n,v_n$
are growing at most exponentially in n. (We may also consider weak Apéry limits when the latter condition on the growth of denominators is dropped.) Although one would definitely like to draw some conclusions about the irrationality of those constants c, this constraint for the arithmetic to be in the sharpest form would severely shorten the existing list of known Apéry limits; for example, it would throw out Catalan’s constant from the list. A very basic question is then as follows.
Question 1. What real numbers can be realised as Apéry limits?
Without going into this in any detail, we present here a (‘weak’) construction of Apéry limits which are related to the L-values of elliptic curves (or of weight two modular forms). The construction emanates from identities, most of which remain conjectural, between the L-values and Mahler measures.
Consider the family of double integrals
 $$ \begin{align*} J_n(z) &=\int_0^1\!\int_0^1\frac{x^{n-1/2}(1-x)^{n-1/2}y^{n-1/2}(1-y)^n}{(1-zxy)^{n+1/2}}\,d x\,d y \\[6pt] &=\frac{\Gamma(n+\tfrac12)^3\Gamma(n+1)}{\Gamma(2n+1)\Gamma(2n+\tfrac32)} \cdot{}_3F_2\bigg(\begin{matrix} n+\tfrac12, \, n+\tfrac12, \, n+\tfrac12 \\ 2n+1, \, 2n+\tfrac32 \end{matrix} \biggm|z\bigg). \end{align*} $$
$$ \begin{align*} J_n(z) &=\int_0^1\!\int_0^1\frac{x^{n-1/2}(1-x)^{n-1/2}y^{n-1/2}(1-y)^n}{(1-zxy)^{n+1/2}}\,d x\,d y \\[6pt] &=\frac{\Gamma(n+\tfrac12)^3\Gamma(n+1)}{\Gamma(2n+1)\Gamma(2n+\tfrac32)} \cdot{}_3F_2\bigg(\begin{matrix} n+\tfrac12, \, n+\tfrac12, \, n+\tfrac12 \\ 2n+1, \, 2n+\tfrac32 \end{matrix} \biggm|z\bigg). \end{align*} $$
Thanks to the nice hypergeometric representation, a recurrence equation satisfied by the double integral can be computed using Zeilberger’s fast summation algorithm [Reference Apagodu and Zeilberger3, Reference Zeilberger14], which is based on the method of creative telescoping. It leads to the third-order recurrence equation:
 $$ \begin{align*} & 4z^4(2n+1)^2(n+1)^2 (16(27z-32)n^4 - 16(69z-86)n^3 \\ &\quad + 8(108z-143)n^2 - 4(55z-76)n + 3(7z-10)) J_{n+1}\\ &\; + z^2(256(3z+8)(27z-32)n^8 - 256(3z+8)(15z-22)n^7 \\ &\;\quad - 64(651z^2+661z-1744)n^6 + 192(59z^2-186)n^5 \\ &\;\quad + 16(1503z^2+697z-3610)n^4 - 16(79z^2-290z+116)n^3 \\ &\;\quad - 4(569z^2-381z-580)n^2 + 4(11z^2-44z+18)n + 3(4z+3)(7z-10)) J_n\\ &\; + 4n(64(3z^2-20z+16)(27z-32)n^7 - 384(3z^2-20z+16)(7z-9)n^6 \\ &\;\quad - 16(411z^3-2698z^2+3988z-1696)n^5 + 64(183z^3-1372z^2+2339z-1134)n^4 \\ &\;\quad + 4(531z^3-1400z^2-424z+1240)n^3 - 8(571z^3-4001z^2+6532z-3060)n^2 \\ &\;\quad + (151z^3-4742z^2+11596z-6888)n + 12(14z^2-29z-30)(z-1)) J_{n-1}\\ &\; + 4n(n-1)(2n-3)^2(z-1)(16(27z-32)n^4 + 48(13z-14)n^3 \\ &\;\quad + 8(18z-11)n^2 - 4(19z-24)n - (7z+6)) J_{n-2} =0. \end{align*} $$
$$ \begin{align*} & 4z^4(2n+1)^2(n+1)^2 (16(27z-32)n^4 - 16(69z-86)n^3 \\ &\quad + 8(108z-143)n^2 - 4(55z-76)n + 3(7z-10)) J_{n+1}\\ &\; + z^2(256(3z+8)(27z-32)n^8 - 256(3z+8)(15z-22)n^7 \\ &\;\quad - 64(651z^2+661z-1744)n^6 + 192(59z^2-186)n^5 \\ &\;\quad + 16(1503z^2+697z-3610)n^4 - 16(79z^2-290z+116)n^3 \\ &\;\quad - 4(569z^2-381z-580)n^2 + 4(11z^2-44z+18)n + 3(4z+3)(7z-10)) J_n\\ &\; + 4n(64(3z^2-20z+16)(27z-32)n^7 - 384(3z^2-20z+16)(7z-9)n^6 \\ &\;\quad - 16(411z^3-2698z^2+3988z-1696)n^5 + 64(183z^3-1372z^2+2339z-1134)n^4 \\ &\;\quad + 4(531z^3-1400z^2-424z+1240)n^3 - 8(571z^3-4001z^2+6532z-3060)n^2 \\ &\;\quad + (151z^3-4742z^2+11596z-6888)n + 12(14z^2-29z-30)(z-1)) J_{n-1}\\ &\; + 4n(n-1)(2n-3)^2(z-1)(16(27z-32)n^4 + 48(13z-14)n^3 \\ &\;\quad + 8(18z-11)n^2 - 4(19z-24)n - (7z+6)) J_{n-2} =0. \end{align*} $$
Furthermore, if we take
 $$ \begin{align*} \lambda(z) &=J_0(z)=2\pi\,{}_3F_2\bigg(\begin{matrix} \tfrac12, \, \tfrac12, \, \tfrac12 \\ 1, \, \tfrac32 \end{matrix} \biggm|z\bigg) =\int_0^1\!\int_0^1\frac{d x\,d y}{\sqrt{x(1-x)y(1-zxy)}}, \\[6pt] \rho_1(z) &=\pi\,{}_2F_1\bigg(\begin{matrix} \tfrac12, \, \tfrac12 \\ 1 \end{matrix} \biggm|z\bigg) =\int_0^1\frac{d x}{\sqrt{x(1-x)(1-zx)}}, \\[6pt] \rho_2(z) &=\pi\,{}_2F_1\bigg(\begin{matrix} -\tfrac12, \, \tfrac12 \\ 1 \end{matrix} \biggm|z\bigg) =\int_0^1\frac{\sqrt{1-zx}}{\sqrt{x(1-x)}}\,d x, \end{align*} $$
$$ \begin{align*} \lambda(z) &=J_0(z)=2\pi\,{}_3F_2\bigg(\begin{matrix} \tfrac12, \, \tfrac12, \, \tfrac12 \\ 1, \, \tfrac32 \end{matrix} \biggm|z\bigg) =\int_0^1\!\int_0^1\frac{d x\,d y}{\sqrt{x(1-x)y(1-zxy)}}, \\[6pt] \rho_1(z) &=\pi\,{}_2F_1\bigg(\begin{matrix} \tfrac12, \, \tfrac12 \\ 1 \end{matrix} \biggm|z\bigg) =\int_0^1\frac{d x}{\sqrt{x(1-x)(1-zx)}}, \\[6pt] \rho_2(z) &=\pi\,{}_2F_1\bigg(\begin{matrix} -\tfrac12, \, \tfrac12 \\ 1 \end{matrix} \biggm|z\bigg) =\int_0^1\frac{\sqrt{1-zx}}{\sqrt{x(1-x)}}\,d x, \end{align*} $$
then
![]() $J_0(z)=\lambda (z)$
,
$J_0(z)=\lambda (z)$
,
 $$ \begin{align*} J_1(z)&=-\frac{3+4z}{4z^2}\,\lambda-\frac{5(1-z)}{z^2}\,\rho_1+ \frac{13}{2z^2}\,\rho_2, \\[6pt] J_2(z)&=\frac{105+480z+64z^2}{64z^4}\,\lambda+\frac{3151-2167z-984z^2}{144z^4}\,\rho_1-\frac{7247+3452z}{288z^4}\,\rho_2. \end{align*} $$
$$ \begin{align*} J_1(z)&=-\frac{3+4z}{4z^2}\,\lambda-\frac{5(1-z)}{z^2}\,\rho_1+ \frac{13}{2z^2}\,\rho_2, \\[6pt] J_2(z)&=\frac{105+480z+64z^2}{64z^4}\,\lambda+\frac{3151-2167z-984z^2}{144z^4}\,\rho_1-\frac{7247+3452z}{288z^4}\,\rho_2. \end{align*} $$
In other words, each
![]() $J_n(z)$
is a
$J_n(z)$
is a
![]() $\mathbb Q(z)$
-linear combination of
$\mathbb Q(z)$
-linear combination of
![]() $\lambda (z),\rho _1(z),\rho _2(z)$
. For
$\lambda (z),\rho _1(z),\rho _2(z)$
. For
![]() $z^{-1}\in \mathbb Z\setminus \{\pm 1\}$
, we find experimentally that the coefficients
$z^{-1}\in \mathbb Z\setminus \{\pm 1\}$
, we find experimentally that the coefficients
![]() $a_n,b_n,c_n$
(depending, of course, on this
$a_n,b_n,c_n$
(depending, of course, on this
![]() $z^{-1}$
) in the representation
$z^{-1}$
) in the representation
satisfy
Now observe that
 $$ \begin{align*} \det\begin{pmatrix} J_n & J_{n+1} \\ c_n & c_{n+1} \end{pmatrix} =\det\begin{pmatrix} a_n & a_{n+1} \\ c_n & c_{n+1} \end{pmatrix}\cdot\lambda(z) +\det\begin{pmatrix} b_n & b_{n+1} \\ c_n & c_{n+1} \end{pmatrix}\cdot\rho_1(z) \end{align*} $$
$$ \begin{align*} \det\begin{pmatrix} J_n & J_{n+1} \\ c_n & c_{n+1} \end{pmatrix} =\det\begin{pmatrix} a_n & a_{n+1} \\ c_n & c_{n+1} \end{pmatrix}\cdot\lambda(z) +\det\begin{pmatrix} b_n & b_{n+1} \\ c_n & c_{n+1} \end{pmatrix}\cdot\rho_1(z) \end{align*} $$
for
![]() $n=0,1,2,\dots .$
The sequences
$n=0,1,2,\dots .$
The sequences
 $$ \begin{align*} A_n=\det\begin{pmatrix} a_n & a_{n+1} \\ c_n & c_{n+1} \end{pmatrix} \quad\text{and}\quad B_n=-\det\begin{pmatrix} b_n & b_{n+1} \\ c_n & c_{n+1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} A_n=\det\begin{pmatrix} a_n & a_{n+1} \\ c_n & c_{n+1} \end{pmatrix} \quad\text{and}\quad B_n=-\det\begin{pmatrix} b_n & b_{n+1} \\ c_n & c_{n+1} \end{pmatrix} \end{align*} $$
satisfy the following third-order (again!) recurrence equation which is the exterior square of the recurrence for
![]() $J_n$
:
$J_n$
:
 $$ \begin{align*} & 4(n+1)(n+2)^2(2n+1)^2(2n+3)^2z^8p_0(n)p_0(n-1) A_{n+1} \\ &\; -4(n+1)^2(2n+1)^2z^4p_0(n-1) (64(3z^2-20z+16)(27z-32)n^7 \\ &\quad + 64(3z^2-20z+16)(147z-170)n^6 + 16(3369z^3-26678z^2+44012z-20576)n^5 \\ &\quad + 16(2457z^3-20918z^2+34376z-15896)n^4 \\ &\quad + 4(843z^3-16808z^2+29432z-13736)n^3 - 4(1445z^3-6794z^2+9600z-4144)n^2 \\ &\quad - (741z^3-6922z^2+10772z-4728)n + z^2(131z-66))A_n \\ &\; -n(2n-1)^2(1-z)z^2p_0(n+1) (256(3z+8)(27z-32)n^8 \\ &\quad - 256(3z+8)(15z-22)n^7 - 64(651z^2+661z-1744)n^6 + 192(59z^2-186)n^5 \\ &\quad + 16(1503z^2+697z-3610)n^4 - 16(79z^2-290z+116)n^3 \\ &\quad - 4(569z^2-381z-580)n^2 + 4(11z^2-44z+18)n + 3(4z+3)(7z-10)) A_{n-1} \\ &\; -4(n-1)n^2(2n-3)^2(2n-1)^2(1-z)^2p_0(n)p_0(n+1) A_{n-2} =0, \end{align*} $$
$$ \begin{align*} & 4(n+1)(n+2)^2(2n+1)^2(2n+3)^2z^8p_0(n)p_0(n-1) A_{n+1} \\ &\; -4(n+1)^2(2n+1)^2z^4p_0(n-1) (64(3z^2-20z+16)(27z-32)n^7 \\ &\quad + 64(3z^2-20z+16)(147z-170)n^6 + 16(3369z^3-26678z^2+44012z-20576)n^5 \\ &\quad + 16(2457z^3-20918z^2+34376z-15896)n^4 \\ &\quad + 4(843z^3-16808z^2+29432z-13736)n^3 - 4(1445z^3-6794z^2+9600z-4144)n^2 \\ &\quad - (741z^3-6922z^2+10772z-4728)n + z^2(131z-66))A_n \\ &\; -n(2n-1)^2(1-z)z^2p_0(n+1) (256(3z+8)(27z-32)n^8 \\ &\quad - 256(3z+8)(15z-22)n^7 - 64(651z^2+661z-1744)n^6 + 192(59z^2-186)n^5 \\ &\quad + 16(1503z^2+697z-3610)n^4 - 16(79z^2-290z+116)n^3 \\ &\quad - 4(569z^2-381z-580)n^2 + 4(11z^2-44z+18)n + 3(4z+3)(7z-10)) A_{n-1} \\ &\; -4(n-1)n^2(2n-3)^2(2n-1)^2(1-z)^2p_0(n)p_0(n+1) A_{n-2} =0, \end{align*} $$
where
and
 $$ \begin{gather*} A_0=\frac{13}{2z^2}, \quad A_1=\frac{395z^2-1051z+591}{72z^6}, \\[6pt] A_2=\frac{15196z^4-201551z^3+548091z^2-543600z+183120}{3600z^{10}} \end{gather*} $$
$$ \begin{gather*} A_0=\frac{13}{2z^2}, \quad A_1=\frac{395z^2-1051z+591}{72z^6}, \\[6pt] A_2=\frac{15196z^4-201551z^3+548091z^2-543600z+183120}{3600z^{10}} \end{gather*} $$
and
 $$ \begin{gather*} B_0=0, \quad B_1=\frac{1117z^2-2299z+1182}{72z^6}, \\[6pt] B_2=\frac{6867z^4-65547z^3+156430z^2-143530z+45780}{450z^{10}}. \end{gather*} $$
$$ \begin{gather*} B_0=0, \quad B_1=\frac{1117z^2-2299z+1182}{72z^6}, \\[6pt] B_2=\frac{6867z^4-65547z^3+156430z^2-143530z+45780}{450z^{10}}. \end{gather*} $$
Furthermore, by construction,
 $$ \begin{align*} \lim_{n\to\infty}\frac{B_n}{A_n}=\frac{\lambda}{\rho_1} \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\frac{B_n}{A_n}=\frac{\lambda}{\rho_1} \end{align*} $$
and, still only experimentally and for
![]() $z^{-1}\in \mathbb Z\setminus \{\pm 1\}$
,
$z^{-1}\in \mathbb Z\setminus \{\pm 1\}$
,
for
![]() $n=0,1,2,\ldots .$
In other words, the number
$n=0,1,2,\ldots .$
In other words, the number
![]() $\lambda /\rho _1$
(but also the quotients
$\lambda /\rho _1$
(but also the quotients
![]() $\lambda /\rho _2$
and
$\lambda /\rho _2$
and
![]() $\rho _1/\rho _2$
) are (weak) Apéry limits for the values of z under consideration.
$\rho _1/\rho _2$
) are (weak) Apéry limits for the values of z under consideration.
For real
![]() $k>0$
with
$k>0$
with
![]() $k^2\in \mathbb Z\setminus \{0,16\}$
, the Mahler measure
$k^2\in \mathbb Z\setminus \{0,16\}$
, the Mahler measure
 $$ \begin{align*} \mu(k) &={\mathrm m}(X+X^{-1}+Y+Y^{-1}+k) \\[6pt] &=\frac1{(2\pi i)^2}\iint\limits_{|X|=|Y|=1}\log|X+X^{-1}+Y+Y^{-1}+k|\,\frac{d X}{X}\,\frac{d Y}{Y} \end{align*} $$
$$ \begin{align*} \mu(k) &={\mathrm m}(X+X^{-1}+Y+Y^{-1}+k) \\[6pt] &=\frac1{(2\pi i)^2}\iint\limits_{|X|=|Y|=1}\log|X+X^{-1}+Y+Y^{-1}+k|\,\frac{d X}{X}\,\frac{d Y}{Y} \end{align*} $$
is expected to be rationally proportional to the L-value
of the elliptic curve
![]() $E=E_k:X+X^{-1}+Y+Y^{-1}+k=0$
of conductor
$E=E_k:X+X^{-1}+Y+Y^{-1}+k=0$
of conductor
![]() $N=N_k=N(E_k)$
. This is actually proven [Reference Brunault and Zudilin5] when
$N=N_k=N(E_k)$
. This is actually proven [Reference Brunault and Zudilin5] when
![]() $k=1$
,
$k=1$
,
![]() $\sqrt 2$
,
$\sqrt 2$
,
![]() $2$
,
$2$
,
![]() $2\sqrt 2$
and
$2\sqrt 2$
and
![]() $3$
for the corresponding elliptic curves 15a8, 56a1, 24a4, 32a1 and 21a4 labelled in accordance with the database [9]; the first number in the label indicates the conductor.
$3$
for the corresponding elliptic curves 15a8, 56a1, 24a4, 32a1 and 21a4 labelled in accordance with the database [9]; the first number in the label indicates the conductor.
For the range
![]() $0<k<4$
,
$0<k<4$
,
 $$ \begin{align*} \mu(k) =\frac k4\cdot{}_3F_2\bigg(\begin{matrix} \tfrac12, \, \tfrac12, \, \tfrac12 \\ 1, \, \tfrac32 \end{matrix}\biggm| \frac{k^2}{16} \bigg), \end{align*} $$
$$ \begin{align*} \mu(k) =\frac k4\cdot{}_3F_2\bigg(\begin{matrix} \tfrac12, \, \tfrac12, \, \tfrac12 \\ 1, \, \tfrac32 \end{matrix}\biggm| \frac{k^2}{16} \bigg), \end{align*} $$
which thus links
![]() $\mu (k)$
to
$\mu (k)$
to
![]() $z^{-1/2}\lambda (z)/\pi $
at
$z^{-1/2}\lambda (z)/\pi $
at
![]() $z=k^2/16$
. Furthermore, the quantity
$z=k^2/16$
. Furthermore, the quantity
![]() $z^{-1/2}\rho _1(z)$
in this case is rationally proportional to the imaginary part of the nonreal period of the same curve, while
$z^{-1/2}\rho _1(z)$
in this case is rationally proportional to the imaginary part of the nonreal period of the same curve, while
![]() $z^{-1/2}\rho _2(z)$
is a
$z^{-1/2}\rho _2(z)$
is a
![]() $\mathbb Q$
-linear combination of the imaginary parts of the nonreal period and the corresponding quasiperiod. This means that, in many cases, we can record
$\mathbb Q$
-linear combination of the imaginary parts of the nonreal period and the corresponding quasiperiod. This means that, in many cases, we can record
![]() $z^{-1/2}\rho _1(z)$
as a rational multiple of the central L-value of a quadratic twist of the curve E. For example, when
$z^{-1/2}\rho _1(z)$
as a rational multiple of the central L-value of a quadratic twist of the curve E. For example, when
![]() $k=2\sqrt 2$
(and hence
$k=2\sqrt 2$
(and hence
![]() $z=1/2$
) the quadratic twist of the elliptic curve of conductor 32 coincides with itself and
$z=1/2$
) the quadratic twist of the elliptic curve of conductor 32 coincides with itself and
From this, we see that the last recursion above with the choice
![]() $z=1/2$
realises the quotient
$z=1/2$
realises the quotient
![]() $L(E,2)/(\pi L(E,1))$
as an Apéry limit for an elliptic curve of conductor 32. When
$L(E,2)/(\pi L(E,1))$
as an Apéry limit for an elliptic curve of conductor 32. When
![]() $k=1$
,
$k=1$
,
for the twist of the elliptic curve by the quadratic character
![]() $\chi _{-4}=\big(\frac{-4}{\cdot}\big)$
; this means that the quotient
$\chi _{-4}=\big(\frac{-4}{\cdot}\big)$
; this means that the quotient
![]() $L(E,2)/(\pi L(E,\chi _{-4},1))$
for an elliptic curve of conductor 15 is realised as an Apéry limit.
$L(E,2)/(\pi L(E,\chi _{-4},1))$
for an elliptic curve of conductor 15 is realised as an Apéry limit.
Clearly, the range
![]() $0<k<4$
has a limited supply of elliptic L-values. When
$0<k<4$
has a limited supply of elliptic L-values. When
![]() $k>4$
, one can write
$k>4$
, one can write
where
 $$ \begin{align*} f(z) &=-\pi\,\bigg(\log\frac{z}{16}+\frac z4\,{}_4F_3\bigg(\begin{matrix} \tfrac32, \, \tfrac32, \, 1, \, 1 \\ 2, \, 2, \, 2 \end{matrix} \biggm|z\bigg) \bigg) \\[6pt] &=-\int_0^1x^{-1/2}(1-x)^{-1/2}\log\frac{1-\sqrt{1-zx}}{1+\sqrt{1-zx}}\,d x \\[6pt] &=\int_0^1\!\int_0^1\frac{x^{-1/2}(1-x)^{-1/2}(1-zx)^{1/2}y^{-1/2}}{1-(1-zx)y}\,d x\,d y \\[6pt] &=Z\int_0^1\!\int_0^1\frac{x^{-1/2}(1-x)^{-1/2}(1-x/Z)^{1/2}(1-y)^{-1/2}}{x(1-y)+yZ}\,d x\,d y, \end{align*} $$
$$ \begin{align*} f(z) &=-\pi\,\bigg(\log\frac{z}{16}+\frac z4\,{}_4F_3\bigg(\begin{matrix} \tfrac32, \, \tfrac32, \, 1, \, 1 \\ 2, \, 2, \, 2 \end{matrix} \biggm|z\bigg) \bigg) \\[6pt] &=-\int_0^1x^{-1/2}(1-x)^{-1/2}\log\frac{1-\sqrt{1-zx}}{1+\sqrt{1-zx}}\,d x \\[6pt] &=\int_0^1\!\int_0^1\frac{x^{-1/2}(1-x)^{-1/2}(1-zx)^{1/2}y^{-1/2}}{1-(1-zx)y}\,d x\,d y \\[6pt] &=Z\int_0^1\!\int_0^1\frac{x^{-1/2}(1-x)^{-1/2}(1-x/Z)^{1/2}(1-y)^{-1/2}}{x(1-y)+yZ}\,d x\,d y, \end{align*} $$
with
![]() $Z=z^{-1}>1$
. At this point, we see that the integrals resemble the integrals
$Z=z^{-1}>1$
. At this point, we see that the integrals resemble the integrals
 $$ \begin{align*} Z^{-l-m}\int_0^1\!\int_0^1\frac{x^j(1-x)^hy^k(1-y)^l}{(x(1-y)+yZ)^{j+k-m+1}}\,d x\,d y, \end{align*} $$
$$ \begin{align*} Z^{-l-m}\int_0^1\!\int_0^1\frac{x^j(1-x)^hy^k(1-y)^l}{(x(1-y)+yZ)^{j+k-m+1}}\,d x\,d y, \end{align*} $$
where
![]() $h,j,k,l,m$
are nonnegative integers, appearing in the linear independence results for the dilogarithm [Reference Rhin and Viola11, Reference Viola and Zudilin12]. This similarity suggests looking at the family
$h,j,k,l,m$
are nonnegative integers, appearing in the linear independence results for the dilogarithm [Reference Rhin and Viola11, Reference Viola and Zudilin12]. This similarity suggests looking at the family
 $$ \begin{align*} L_n(Z)=\int_0^1\!\int_0^1\frac{x^{n-1/2}(1-x)^{2n-1/2}(1-x/Z)^{1/2}y^n(1-y)^{n-1/2}}{(x(1-y)+yZ)^{n+1}}\, d x\, d y, \end{align*} $$
$$ \begin{align*} L_n(Z)=\int_0^1\!\int_0^1\frac{x^{n-1/2}(1-x)^{2n-1/2}(1-x/Z)^{1/2}y^n(1-y)^{n-1/2}}{(x(1-y)+yZ)^{n+1}}\, d x\, d y, \end{align*} $$
where
![]() $Z=z^{-1}$
is a large (positive) integer. We tackle this double integral by iterated applications of creative telescoping: while the first integration (regardless of whether one starts with x or with y) can be done with the Almkvist–Zeilberger algorithm, the second one requires more general holonomic methods, since the integrand is no longer hyperexponential. Using the Mathematica package HolonomicFunctions [Reference Koutschan8], where these algorithms are implemented, we find that the integral
$Z=z^{-1}$
is a large (positive) integer. We tackle this double integral by iterated applications of creative telescoping: while the first integration (regardless of whether one starts with x or with y) can be done with the Almkvist–Zeilberger algorithm, the second one requires more general holonomic methods, since the integrand is no longer hyperexponential. Using the Mathematica package HolonomicFunctions [Reference Koutschan8], where these algorithms are implemented, we find that the integral
![]() $L_n(Z)$
satisfies a lengthy fourth-order recurrence equation. Moreover, it turns out that
$L_n(Z)$
satisfies a lengthy fourth-order recurrence equation. Moreover, it turns out that
![]() $L_n(Z)$
is a
$L_n(Z)$
is a
![]() $\mathbb Q(Z)$
-linear combination of
$\mathbb Q(Z)$
-linear combination of
![]() $\rho _1=\rho _1(1/Z)$
,
$\rho _1=\rho _1(1/Z)$
,
![]() $\rho _2=\rho _2(1/Z)$
,
$\rho _2=\rho _2(1/Z)$
,
![]() $\sigma _1=L_0(Z)$
and
$\sigma _1=L_0(Z)$
and
 $$ \begin{align*} \sigma_2=\sigma_2(Z) =\int_0^1\!\int_0^1\frac{x^{-1/2}(1-x)^{1/2}(1-x/Z)^{1/2}(1-y)^{1/2}}{x(1-y)+yZ}\,d x\,d y. \end{align*} $$
$$ \begin{align*} \sigma_2=\sigma_2(Z) =\int_0^1\!\int_0^1\frac{x^{-1/2}(1-x)^{1/2}(1-x/Z)^{1/2}(1-y)^{1/2}}{x(1-y)+yZ}\,d x\,d y. \end{align*} $$
One can produce a recurrence equation out of the one for
![]() $L_n(Z)$
to cast, for example,
$L_n(Z)$
to cast, for example,
![]() $\sigma _1/\rho _1$
as an Apéry limit. Because this finding does not meet any reasonable aesthetic requirements and does not imply anything (to be claimed) irrational, we do not include it in this article.
$\sigma _1/\rho _1$
as an Apéry limit. Because this finding does not meet any reasonable aesthetic requirements and does not imply anything (to be claimed) irrational, we do not include it in this article.