Article contents
CONGRUENCES FOR THE 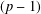 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
Published online by Cambridge University Press: 28 November 2018
Abstract
We prove two conjectural congruences on the 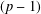 $(p-1)$th Apéry number, which were recently proposed by Z.-H. Sun.
$(p-1)$th Apéry number, which were recently proposed by Z.-H. Sun.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the National Natural Science Foundation of China (grant 11801417).
References
- 5
- Cited by


