Research Article
Metacyclic Invariants of Knots and Links
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 193-201
-
- Article
-
- You have access
- Export citation
On Absolute Summability by Riesz and Generalized Cesàro Means. I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-208
-
- Article
-
- You have access
- Export citation
On Absolute Summability by Riesz and Generalized Cesàro Means. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 209-218
-
- Article
-
- You have access
- Export citation
A Characterization of the Approximately Continuous Denjoy Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 219-226
-
- Article
-
- You have access
- Export citation
Compositions of Set Operations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 227-234
-
- Article
-
- You have access
- Export citation
Cell Complexes, Valuations, and the Euler Relation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 235-241
-
- Article
-
- You have access
- Export citation
Galois Extensions as Modules over the Group Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 242-248
-
- Article
-
- You have access
- Export citation
On Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 249-254
-
- Article
-
- You have access
- Export citation
Point-Transitive Actions by the Unit Interval
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-259
-
- Article
-
- You have access
- Export citation
Singular Integrals are Perron Integrals of a Certain Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 260-264
-
- Article
-
- You have access
- Export citation
Polytopes with an Axis Of Symmetry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-287
-
- Article
-
- You have access
- Export citation
Un Théorème De Régularité Pour Une Équation Différentielle Abstraite
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 288-296
-
- Article
-
- You have access
- Export citation
On the Integral Extensions of Quadratic Forms Over Local Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-307
-
- Article
-
- You have access
- Export citation
Extensions of Certain Maps to Automorphisms of m
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 308-316
-
- Article
-
- You have access
- Export citation
On the Simplex of Completely Monotonic Functions on a Commutative Semigroup
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-326
-
- Article
-
- You have access
- Export citation
M-Primary Elements of a Local Noether Lattice
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-331
-
- Article
-
- You have access
- Export citation
Homotopy of Natural Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 332-341
-
- Article
-
- You have access
- Export citation
On the Zeros of Functions with Derivatives in H1 and H∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 342-347
-
- Article
-
- You have access
- Export citation
A Generalization of Commutative and Alternative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 348-362
-
- Article
-
- You have access
- Export citation
On the Vanishing of a (G, σ) Product in a (G, σ) Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 363-371
-
- Article
-
- You have access
- Export citation

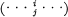 , and this property characterizes
, and this property characterizes 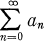
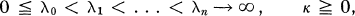
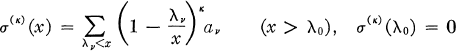
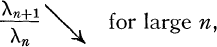

 ).
).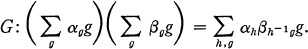
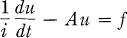
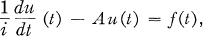
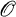 and unique prime ideal (
and unique prime ideal (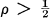 , then
, then