Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-04-30T15:31:44.112Z Has data issue: false hasContentIssue false
  • English
  • Français

A sharpened form of Adams-type inequalities on higher-order Sobolev spaces 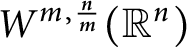$W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach

Part of: Partial differential equations Linear function spaces and their duals Elliptic equations and systems Harmonic analysis in several variables

Published online by Cambridge University Press:  15 December 2021

Lu Chen ,
Guozhen Lu  and
Maocun Zhu
Lu Chen
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing 100081, P. R. China e-mail: chenlu5818804@163.com
Guozhen Lu*
Affiliation:
Department of Mathematics, University of Connecticut Storrs, CT 06269, USA
Maocun Zhu
Affiliation:
Faculty of Science, Jiangsu University, Zhenjiang 212013, P. R. China e-mail: zhumaochun2006@126.com
*
e-mail: guozhen.lu@uconn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we develop an extremely simple method to establish the sharpened Adams-type inequalities on higher-order Sobolev spaces 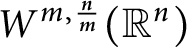$W^{m,\frac {n}{m}}(\mathbb {R}^n)$ in the entire space 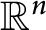$\mathbb {R}^n$ , which can be stated as follows: Given 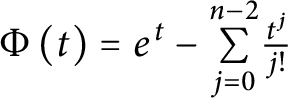$\Phi \left ( t\right ) =e^{t}-\underset {j=0}{\overset {n-2}{\sum }} \frac {t^{j}}{j!}$ and the Adams sharp constant 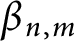$\beta _{n,m}$ . Then,

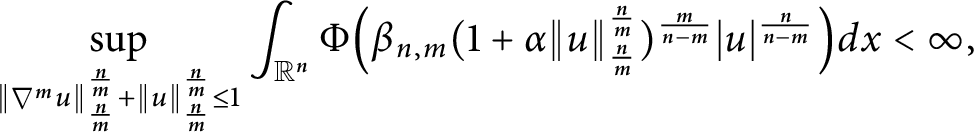$$ \begin{align*}\sup_{\|\nabla^mu\|_{\frac{n}{m}}^{\frac{n}{m}}+\|u\|_{\frac{n}{m}}^{\frac{n}{m}}\leq1}\int_{\mathbb{R}^n}\Phi\Big(\beta_{n,m} (1+\alpha \|u\|_{\frac{n}{m}}^{\frac{n}{m}} )^{\frac{m}{n-m}}|u|^{\frac{n}{n-m}}\Big)dx<\infty, \end{align*} $$
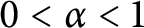for any $0<\alpha <1$ . Furthermore, we construct a proper test function sequence to derive the sharpness of the exponent 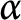$\alpha $ of the above Adams inequalities. Namely, we will show that if 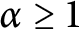$\alpha \ge 1$ , then the above supremum is infinite.

Our argument avoids applying the complicated blow-up analysis often used in the literature to deal with such sharpened inequalities.

Keywords

Adams inequalitiesbest constantsrearrangement-free argumentMoser-Trudinger inequalities

MSC classification

Primary: 42B35: Function spaces arising in harmonic analysis
Secondary: 42B37: Harmonic analysis and PDE 35J91: Semilinear elliptic equations with Laplacian, bi-Laplacian or poly-Laplacian 35B33: Critical exponents 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 895 - 905
Check for updates
Copyright
© Canadian Mathematical Society, 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported partly by the National Natural Science Foundation of China (No. 11901031). The second author was supported partly by the Simons Foundation. The third author was supported partly by the National Natural Science Foundation of China (No. 12071185).

References

Adams, D., A sharp inequality of J. Moser for higher order derivatives. Ann. of Math. (2) 128(1998), 383–398.Google Scholar
Druet, O. Adimurthi, Blow-up analysis in dimension 2 and a sharp form of Trudinger–Moser inequality. Comm. Partial Differential Equations 29(2004), 295–322.Google Scholar
Chen, L., Lu, G., and Zhu, M., Sharpened Trudinger–Moser inequalities on the Euclidean space and Heisenberg group. J. Geom. Anal. 31(2021), no. 12, 12155–12181.CrossRefGoogle Scholar
Chen, L., Lu, G., and Zhu, M., Sharp Trudinger–Moser inequality and ground state solutions to quasi-linear Schrödinger equations with degenerate potentials in Rn . Adv. Nonlinear Stud. 21(2021), no. 4, 733–749.10.1515/ans-2021-2146CrossRefGoogle Scholar
Cohn, W. and Lu, G., Best constants for Moser–Trudinger inequalities on the Heisenberg group. Indiana Univ. Math. J. 50(2001), no. 4, 1567–1591.CrossRefGoogle Scholar
Fontana, L. and Morpurgo, C., Sharp exponential integrability for critical Riesz potentials and fractional Laplacians on ℝ n . Nonlinear Anal. 167(2018), 85–122.CrossRefGoogle Scholar
Lam, N. and Lu, G., Sharp Moser–Trudinger inequality on the Heisenberg group at the critical case and applications. Adv. Math. 231(2012), 3259–3287.CrossRefGoogle Scholar
Lam, N. and Lu, G., Sharp Adams type inequalities in Sobolev spaces ${W}^{m,\frac{n}{m}}\left({\mathbb{R}}^n\right)$ for arbitrary integer m. J. Differential Equations 253(2012), no. 4, 1143–1171.CrossRefGoogle Scholar
Lam, N. and Lu, G., A new approach to sharp Moser–Trudinger and Adams type inequalities: a rearrangement-free argument. J. Differential Equations 255(2013), 298–325.CrossRefGoogle Scholar
Lam, N., Lu, G., and Tang, H., Sharp subcritical Moser–Trudinger inequalities on Heisenberg groups and subelliptic PDEs. Nonlinear Anal. 95(2014), 77–92.CrossRefGoogle Scholar
Lam, N., Lu, G., and Zhang, L., Equivalence of critical and subcritical sharp Trudinger–Moser–Adams inequalities. Rev. Mat. Iberoam. 33(2017), no. 4, 1219–1246.CrossRefGoogle Scholar
Lam, N., Lu, G., and Zhang, L., Sharp singular Trudinger–Moser inequalities under different norms. Adv. Nonlinear Stud. 19(2019), no. 2, 239–261.CrossRefGoogle Scholar
Li, J., Lu, G., and Zhu, M., Concentration-compactness principle for Trudinger–Moser inequalities on Heisenberg groups and existence of ground state solutions. Calc. Var. Partial Differential Equations 57(2018), no. 3, 26. https://doi.org/10.1007/s00526-018-1352-8 CrossRefGoogle Scholar
Li, J., Lu, G., and Zhu, M., Concentration-compactness principle for Trudinger–Moser’s inequalities on Riemannian manifolds and Heisenberg groups: a completely symmetrization-free argument. Adv. Nonlinear Stud. 21(2021), no. 4, 917–937.10.1515/ans-2021-2147CrossRefGoogle Scholar
Li, Y. X. and Ruf, B., A sharp Moser–Trudinger type inequality for unbounded domains in ℝn . Indiana Univ. Math. J. 57(2008), 451–480.CrossRefGoogle Scholar
Lu, G. and Yang, Y., Adams’ inequalities for bi-Laplacian and extremal functions in dimension four. Adv. Math. 220(2009), no. 4, 1135–1170.CrossRefGoogle Scholar
Lu, G. and Zhu, M., A sharp Trudinger–Moser type inequality involving Ln norm in the entire space ℝn . J. Differential Equations 267(2019), no. 5, 3046–3082.CrossRefGoogle Scholar
Moser, J., A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20(1970), 1077–1092.CrossRefGoogle Scholar
O’Neil, R., Convolution operators and L(p, q) spaces. Duke Math. J. 30(1963), 129–142.CrossRefGoogle Scholar
Pohožaev, S. I., On the Sobolev embedding theorem for pl = n . In: Doklady conference, Moscow Power Institute, Moscow, 1965, pp. 158–170.Google Scholar
Ruf, B., A sharp Moser–Trudinger type inequality for unbounded domains in ℝ 2. J. Funct. Anal. 219(2005), 340–367.CrossRefGoogle Scholar
Ruf, B. and Sani, F., Sharp Adams-type inequalities in Rn . Trans. Amer. Math. Soc. 365(2013), no. 2, 645–670.10.1090/S0002-9947-2012-05561-9CrossRefGoogle Scholar
Trudinger, N. S., On imbeddings into Orlicz spaces and some applications. J. Math. Mech. 17(1967), 473–483.Google Scholar
Yang, Y., A sharp form of Moser–Trudinger inequality in high dimension. J. Funct. Anal. 239(2006), no. 1, 100–126.CrossRefGoogle Scholar
Yudovič, V. I., Some estimates connected with integral operators and with solutions of elliptic equations. Dokl. Akad. Nauk SSSR. 138(1961), 805–808 (in Russian).Google Scholar
Zhang, C. and Chen, L., Concentration-compactness principle of singular Trudinger–Moser inequalities in ℝn and n-Laplace equations. Adv. Nonlinear Stud. 18(2018), 567–585.10.1515/ans-2017-6041CrossRefGoogle Scholar