Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-29T06:50:37.429Z Has data issue: false hasContentIssue false
  • English
  • Français

A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution

Part of: Combinatorial probability Sequences and sets Other special functions Limit theorems Markov processes

Published online by Cambridge University Press:  22 November 2021

Martin Möhle
Martin Möhle*
Affiliation:
Eberhard Karls Universität Tübingen
*
*Postal address: Mathematisches Institut, Eberhard Karls Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany. Email address: martin.moehle@uni-tuebingen.de
Get access Rights & Permissions [Opens in a new window]

Abstract

In addition to the features of the two-parameter Chinese restaurant process (CRP), the restaurant under consideration has a cocktail bar and hence allows for a wider range of (bar and table) occupancy mechanisms. The model depends on three real parameters, $\alpha$ , 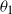$\theta_1$ , and 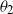$\theta_2$ , fulfilling certain conditions. Results known for the two-parameter CRP are carried over to this model. We study the number of customers at the cocktail bar, the number of customers at each table, and the number of occupied tables after n customers have entered the restaurant. For 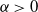$\alpha>0$ the number of occupied tables, properly scaled, is asymptotically three-parameter Mittag–Leffler distributed as n tends to infinity. We provide representations for the two- and three-parameter Mittag–Leffler distribution leading to efficient random number generators for these distributions. The proofs draw heavily from methods known for exchangeable random partitions, martingale methods known for generalized Pólya urns, and results known for the two-parameter CRP.

Keywords

Beta distributionexchangeabilityoccupied tablesPólya urnrandom number generationrandom partitionrejection methodrestaurant processStirling numbersthree-parameter Mittag–Leffler distribution

MSC classification

Primary: 60C05: Combinatorial probability 60F05: Central limit and other weak theorems
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 33E12: Mittag-Leffler functions and generalizations 11B73: Bell and Stirling numbers
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 4 , December 2021 , pp. 978 - 1006
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. J. (1985). Exchangeability and Related Topics (Lect. Notes Math. 1117). Springer, New York.10.1007/BFb0099421CrossRefGoogle Scholar
Antoniak, C. E. (1974). Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. Ann. Statist. 2, 1152–1174.10.1214/aos/1176342871CrossRefGoogle Scholar
Billingsley, P. (1995). Probability and Measure, 3rd edn. Wiley, New York.Google Scholar
Blackwell, D. and MacQueen, J. B. (1973). Ferguson distributions via Pólya urn schemes. Ann. Statist. 1, 353–355.10.1214/aos/1176342372CrossRefGoogle Scholar
Chambers, J. M., Mallows, C. L. and Stuck, B. W. (1976). A method for simulating stable random variables. J. Am. Stat. Assoc. 71, 340–344.10.1080/01621459.1976.10480344CrossRefGoogle Scholar
Devroye, L. (1986). Non-Uniform Random Variate Generation. Springer, New York.10.1007/978-1-4613-8643-8CrossRefGoogle Scholar
Donnelly, P. J. (1986). Partition structures, Pólya urns, the Ewens sampling formula and the ages of alleles. Theor. Popul. Biol. 30, 271–288.10.1016/0040-5809(86)90037-7CrossRefGoogle Scholar
Ewens, W. J. (1972). The sampling theory of selectively neutral alleles. Theor. Popul. Biol. 3, 87–112.10.1016/0040-5809(72)90035-4CrossRefGoogle ScholarPubMed
Feller, W. (1971). An Introduction to Probability and Its Applications, Vol. II. Wiley, New York.Google Scholar
Flajolet, P., Dumas, P. and Puyhaubert, V. (2006). Some exactly solvable models of urn process theory. Discrete Math. Theor. Comp. Sci. AG, 59–118.Google Scholar
Green, P. J. (2010). Colouring and breaking sticks: Random distributions and heterogeneous clustering. In Probability and Mathematical Genetics: Papers in Honour of Sir John Kingman, eds. Bingham, N. H. and Goldie, C. M.. Cambridge University Press, pp. 319–344.10.1017/CBO9781139107174.015CrossRefGoogle Scholar
Hoppe, F. M. (1984). Pólya-like urns and the Ewens sampling formula. J. Math. Biol. 20, 91–94.10.1007/BF00275863CrossRefGoogle Scholar
Hoppe, F. M. (1987). The sampling theory of neutral alleles and an urn model in population genetics. J. Math. Biol. 25, 123–159.10.1007/BF00276386CrossRefGoogle Scholar
Hsu, L. C. and Shiue, P. J.-S. (1998). A unified approach to generalized Stirling numbers. Adv. Appl. Math. 20, 366–384.10.1006/aama.1998.0586CrossRefGoogle Scholar
Ibragimov, I. A. and Chernin, K. E. (1959). On the unimodality of stable laws. Teor. Veroyatnost. i Primenen 4, 453–456. English translation: Theor. Prob. Appl. 4, 417–419 (1959).10.1137/1104043CrossRefGoogle Scholar
James, L. F. (2002). Poisson process partition calculus with applications to exchangeable models and Bayesian nonparametrics. arXiv:math/0205093.Google Scholar
James, L. F. (2005). Bayesian Poisson process partition calculus with an application to Bayesian Lévy moving averages. Ann. Statist. 33, 1771–1799.10.1214/009053605000000336CrossRefGoogle Scholar
Janson, S. (2004). Functional limit theorems for multitype branching processes and generalized Pólya urns. Stoch. Proc. Appl. 110, 177–245.10.1016/j.spa.2003.12.002CrossRefGoogle Scholar
Janson, S. (2006). Limit theorems for triangular urn schemes. Prob. Theory Relat. Fields 134, 417–452.10.1007/s00440-005-0442-7CrossRefGoogle Scholar
Kallenberg, O. (2002). Foundations of Modern Probability, 2nd edn. Springer, New York.10.1007/978-1-4757-4015-8CrossRefGoogle Scholar
Kanter, M. (1975). Stable densities under change of scale and total variation inequalities. Ann. Prob. 3, 697–707.10.1214/aop/1176996309CrossRefGoogle Scholar
Kingman, J. F. C. (1978). Random partitions in population genetics. Proc. R. Soc. London A, 361, 1–20.Google Scholar
Lo, A. Y., Brunner, L. J. and Chan, A. T. (1996). Weighted Chinese restaurant processes and Bayesian mixture models. Research report, Hong Kong University of Science and Technology. Available at http://www.utstat.utoronto.ca/~brunner/papers/wcr96.pdf. Google Scholar
Mikusiński, J. (1959). On the function whose Laplace transform is $\textrm{e}^{-s^a}$ . Studia Math. 18, 191–198.10.4064/sm-18-2-191-198CrossRefGoogle Scholar
Möhle, M. (2006). On sampling distributions for coalescent processes with simultaneous multiple collisions. Bernoulli 12, 35–53.Google Scholar
Petrov, V. V. (1975). Sums of Independent Random Variables. Springer, Berlin.10.1007/978-3-642-65809-9CrossRefGoogle Scholar
Pitman, J. (1995). Exchangeable and partially exchangeable random partitions. Prob. Theory Relat. Fields 102, 145–158.10.1007/BF01213386CrossRefGoogle Scholar
Pitman, J. (1996). Random discrete distributions invariant under size-biased permutation. Adv. Appl. Prob. 28, 525–539.10.2307/1428070CrossRefGoogle Scholar
Pitman, J. (2003). Poisson–Kingman partitions. In Statistics and Science: A Festschrift for Terry Speed, eds. Speed, T. P. and Goldstein, D. R. (IMS Lect. Notes Monogr. Ser. 40). Institute of Mathematical Statistics, Beechwood, OH, pp. 1–34.10.1214/lnms/1215091133CrossRefGoogle Scholar
Pitman, J. (2006). Combinatorial Stochastic Processes (Lect. Notes Math. 1875). Springer, Berlin.Google Scholar
Pitman, J. and Yor, M. (1997). The two-parameter Poisson–Dirichlet distribution derived from a stable subordinator. Ann. Prob. 25, 855–900.10.1214/aop/1024404422CrossRefGoogle Scholar
Prabhakar, T. R. (1971). A singular integral equation with a generalized Mittag–Leffler function in the kernel. Yokohama Math. J. 19, 7–15.Google Scholar
Schmelzer, T. and Trefethen, L. N. (2007). Computing the gamma function using contour integrals and related approximations. SIAM J. Numer. Anal. 45, 558–571.10.1137/050646342CrossRefGoogle Scholar
Siegmund, D. (1976). The equivalence of absorbing and reflecting barrier problems for stochastically monotone Markov processes. Ann. Prob. 4, 914–924.10.1214/aop/1176995936CrossRefGoogle Scholar
Stanković, B. (1954). Sur une fonction du calcul opérationnel. Acad. Serbe Sci. Pub. Inst. Math. 6, 75–78.Google Scholar
Stanković, B. (1970). On the function of E. M. Wright. Pub. Inst. Math. Beograd N.S. 10, 113–124.Google Scholar
Steutel, F. W. and Van Harn, K. (2004). Infinite Divisibility of Probability Distributions on the Real Line. Marcel Dekker Inc., New York.Google Scholar
Temme, N. M. (1978). The Numerical Computation of Special Functions by Use of Quadrature Rules for Saddle Point Integrals. II. Gamma Functions, Modified Bessel Functions and Parabolic Cylinder Functions. Mathematisch Centrum, Afdeling Toegepaste Wiskunde, Amsterdam.Google Scholar
Temme, N. M. (1996). Special Functions. Wiley, New York.10.1002/9781118032572CrossRefGoogle Scholar
Tomovski, Ž., Pogány, T. K. and Srivastava, H. M. (2014). Laplace type integral expressions for a certain three-parameter family of generalized Mittag-Leffler functions with applications involving complete monotonicity. J. Franklin Inst. 351, 5437–5454.10.1016/j.jfranklin.2014.09.007CrossRefGoogle Scholar
Trieb, G. (1992). A Pólya urn model and the coalescent. J. Appl. Prob. 29, 1–10.10.2307/3214786CrossRefGoogle Scholar
Zhang, P., Chen, C. and Mahmoud, H. (2015). Explicit characterization of moments of balanced triangular Pólya urns by an elementary approach. Statist. Prob. Lett. 96, 149–153.10.1016/j.spl.2014.09.016CrossRefGoogle Scholar