Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Froitzheim, A.
Merbold, S.
and
Egbers, C.
2017.
Velocity profiles, flow structures and scalings in a wide-gap turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
330.
Zhu, Bihai
Ji, Zengqi
Lou, Zhengkun
and
Qian, Pengcheng
2018.
Torque scaling in small-gap Taylor-Couette flow with smooth or grooved wall.
Physical Review E,
Vol. 97,
Issue. 3,
Ezeta, Rodrigo
Huisman, Sander G.
Sun, Chao
and
Lohse, Detlef
2018.
Turbulence strength in ultimate Taylor–Couette turbulence.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
397.
Elghobashi, Said
2019.
Direct Numerical Simulation of Turbulent Flows Laden with Droplets or Bubbles.
Annual Review of Fluid Mechanics,
Vol. 51,
Issue. 1,
p.
217.
Sacco, Francesco
Verzicco, Roberto
and
Ostilla-Mónico, Rodolfo
2019.
Dynamics and evolution of turbulent Taylor rolls.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
970.
Froitzheim, Andreas
Ezeta, Rodrigo
Huisman, Sander G.
Merbold, Sebastian
Sun, Chao
Lohse, Detlef
and
Egbers, Christoph
2019.
Statistics, plumes and azimuthally travelling waves in ultimate Taylor–Couette turbulent vortices.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
733.
Berghout, Pieter
Verzicco, Roberto
Stevens, Richard J. A. M.
Lohse, Detlef
and
Chung, Daniel
2020.
Calculation of the mean velocity profile for strongly turbulent Taylor–Couette flow at arbitrary radius ratios.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Berghout, Pieter
Bullee, Pim A.
Fuchs, Thomas
Scharnowski, Sven
Kähler, Christian J.
Chung, Daniel
Lohse, Detlef
and
Huisman, Sander G.
2021.
Characterizing the turbulent drag properties of rough surfaces with a Taylor–Couette set-up.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Leng, X.-Y.
Krasnov, D.
Li, B.-W.
and
Zhong, J.-Q.
2021.
Flow structures and heat transport in Taylor–Couette systems with axial temperature gradient.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Leng, X.-Y.
and
Zhong, J.-Q.
2022.
Aspect-ratio dependence of heat and angular momentum transport in turbulent Taylor-Couette flows with axial thermal forcing.
International Journal of Heat and Mass Transfer,
Vol. 195,
Issue. ,
p.
123194.
Leng, X.-Y.
and
Zhong, J.-Q.
2022.
Mutual coherent structures for heat and angular momentum transport in turbulent Taylor-Couette flows.
Physical Review Fluids,
Vol. 7,
Issue. 4,
Khawar, Obaidullah
Baig, M.F.
and
Sanghi, Sanjeev
2022.
Counter-rotating Taylor-Couette flows with radial temperature gradient.
International Journal of Heat and Fluid Flow,
Vol. 95,
Issue. ,
p.
108980.
Balonishnikov, Alexander
and
Kruchkova, Julia
2022.
Resistance law dependence on radius ratios for turbulent Taylor-Couette flow from extended local balance model.
IOP Conference Series: Materials Science and Engineering,
Vol. 1227,
Issue. 1,
p.
012001.
Zhang, Shengqi
Xia, Zhenhua
and
Chen, Shiyi
2022.
Flow structures in spanwise rotating plane Poiseuille flow based on thermal analogy.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Hamede, Mohammed Hussein
Merbold, Sebastian
and
Egbers, Christoph
2023.
Experimental investigation of turbulent counter-rotating Taylor–Couette flows for radius ratio η = 0.1.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Hamede, Mohammed Hussein
Merbold, Sebastian
and
Egbers, Christoph
2023.
Experimental method for investigating the formation of flow patterns in a very wide gap Taylor-Couette flow (η = 0.1)..
tm - Technisches Messen,
Vol. 90,
Issue. 5,
p.
332.
Liu, Xiaochao
You, Chenxi
Cao, Yanlin
Xu, Baorui
Yang, Yantao
Li, Hongyuan
Lv, Pengyu
Sun, Chao
and
Duan, Huiling
2024.
Friction drag reduction of Taylor–Couette flow over air-filled microgrooves.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Kang, Changwoo
Talioua, Abdessamad
Prigent, Arnaud
and
Mutabazi, Innocent
2025.
Transition from featureless turbulence to turbulent Taylor vortices in counter-rotating cylindrical annulus.
Physics of Fluids,
Vol. 37,
Issue. 2,
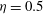 ${\it\eta}=0.5$ : scaling, flow structures and plumes
${\it\eta}=0.5$ : scaling, flow structures and plumes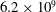 $6.2\times 10^{9}$ . The extracted angular velocity profiles follow a log law more closely than the azimuthal velocity profiles due to the strong curvature of this
$6.2\times 10^{9}$ . The extracted angular velocity profiles follow a log law more closely than the azimuthal velocity profiles due to the strong curvature of this 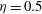 ${\it\eta}=0.5$ set-up. The scaling of the wind Reynolds number with the Taylor number agrees with the theoretically predicted
${\it\eta}=0.5$ set-up. The scaling of the wind Reynolds number with the Taylor number agrees with the theoretically predicted 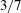 $3/7$ scaling for the classical turbulent regime, which is much more pronounced than for the well-explored
$3/7$ scaling for the classical turbulent regime, which is much more pronounced than for the well-explored 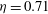 ${\it\eta}=0.71$ case, for which the ultimate regime sets in at much lower Taylor number. By measuring at varying axial positions, roll structures are found for counter-rotation while no clear coherent structures are seen for pure inner cylinder rotation. In addition, turbulent plumes coming from the inner and outer cylinders are investigated. For pure inner cylinder rotation, the plumes in the radial velocity move away from the inner cylinder, while the plumes in the azimuthal velocity mainly move away from the outer cylinder. For counter-rotation, the mean radial flow in the roll structures strongly affects the direction and intensity of the turbulent plumes. Furthermore, it is experimentally confirmed that, in regions where plumes are emitted, boundary layer profiles with a logarithmic signature are created.
${\it\eta}=0.71$ case, for which the ultimate regime sets in at much lower Taylor number. By measuring at varying axial positions, roll structures are found for counter-rotation while no clear coherent structures are seen for pure inner cylinder rotation. In addition, turbulent plumes coming from the inner and outer cylinders are investigated. For pure inner cylinder rotation, the plumes in the radial velocity move away from the inner cylinder, while the plumes in the azimuthal velocity mainly move away from the outer cylinder. For counter-rotation, the mean radial flow in the roll structures strongly affects the direction and intensity of the turbulent plumes. Furthermore, it is experimentally confirmed that, in regions where plumes are emitted, boundary layer profiles with a logarithmic signature are created.

