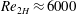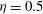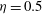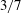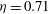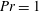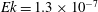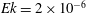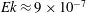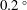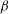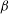Contents
Papers
Numerical characterization of three-dimensional bluff body shear layer behaviour
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 1-26
-
- Article
- Export citation
Convective plumes in rotating systems
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 27-55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Using adjoint-based optimization to study kinematics and deformation of flapping wings
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 56-99
-
- Article
- Export citation
Effect of confinement in wall-bounded non-colloidal suspensions
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 100-127
-
- Article
- Export citation
On the effects of vertical offset and core structure in streamwise-oriented vortex–wing interactions
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 128-158
-
- Article
- Export citation
Spectral modelling for passive scalar dynamics in homogeneous anisotropic turbulence
-
- Published online by Cambridge University Press:
- 22 June 2016, pp. 159-199
-
- Article
- Export citation
Three-dimensional organisation of primary and secondary crossflow instability
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 200-245
-
- Article
- Export citation
Turbulent 2.5-dimensional dynamos
-
- Published online by Cambridge University Press:
- 22 June 2016, pp. 246-264
-
- Article
- Export citation
Baroclinic instability of axially symmetric flow over sloping bathymetry
-
- Published online by Cambridge University Press:
- 22 June 2016, pp. 265-296
-
- Article
- Export citation
Groove-induced changes of discharge in channel flows
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 297-333
-
- Article
- Export citation
Taylor–Couette turbulence at radius ratio
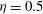 ${\it\eta}=0.5$ : scaling, flow structures and plumes
${\it\eta}=0.5$ : scaling, flow structures and plumes
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 334-351
-
- Article
- Export citation
A Lagrangian study of turbulent mixing: forward and backward dispersion of molecular trajectories in isotropic turbulence
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 352-382
-
- Article
- Export citation
Unsteadiness in a large turbulent separation bubble
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 383-412
-
- Article
- Export citation
Transition to geostrophic convection: the role of the boundary conditions
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 413-432
-
- Article
- Export citation
Lubrication of soft viscoelastic solids
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 433-447
-
- Article
- Export citation
Convection at an isothermal wall in an enclosure and establishment of stratification
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 448-475
-
- Article
- Export citation
Free instability of channel bifurcations and morphodynamic influence
-
- Published online by Cambridge University Press:
- 28 June 2016, pp. 476-504
-
- Article
- Export citation
Turbulence attenuation in simultaneously heated and cooled annular flows at supercritical pressure
-
- Published online by Cambridge University Press:
- 28 June 2016, pp. 505-540
-
- Article
- Export citation
Transport and instability in driven two-dimensional magnetohydrodynamic flows
-
- Published online by Cambridge University Press:
- 28 June 2016, pp. 541-578
-
- Article
- Export citation
Linear stability of Hill’s vortex to axisymmetric perturbations
-
- Published online by Cambridge University Press:
- 28 June 2016, pp. 579-602
-
- Article
- Export citation