Hostname: page-component-54dcc4c588-sq2k7 Total loading time: 0 Render date: 2025-09-30T08:33:48.438Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to geostrophic convection: the role of the boundary conditions

Published online by Cambridge University Press:  23 June 2016

Rudie P. J. Kunnen ,
Rodolfo Ostilla-Mónico ,
Erwin P. van der Poel ,
Roberto Verzicco  and
Detlef Lohse
Rudie P. J. Kunnen*
Affiliation:
Fluid Dynamics Laboratory, Department of Applied Physics, and J. M. Burgers Centre for Fluid Dynamics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
Rodolfo Ostilla-Mónico
Affiliation:
Physics of Fluids Group, Mesa+ Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Erwin P. van der Poel
Affiliation:
Physics of Fluids Group, Mesa+ Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids Group, Mesa+ Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Detlef Lohse
Affiliation:
Physics of Fluids Group, Mesa+ Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: r.p.j.kunnen@tue.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

Rotating Rayleigh–Bénard convection, the flow in a rotating fluid layer heated from below and cooled from above, is used to analyse the transition to the geostrophic regime of thermal convection. In the geostrophic regime, which is of direct relevance to most geo- and astrophysical flows, the system is strongly rotating while maintaining a sufficiently large thermal driving to generate turbulence. We directly simulate the Navier–Stokes equations for two values of the thermal forcing, i.e. 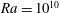$Ra=10^{10}$ and 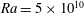$Ra=5\times 10^{10}$ , at constant Prandtl number 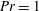$Pr=1$ , and vary the Ekman number in the range 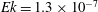$Ek=1.3\times 10^{-7}$ to 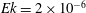$Ek=2\times 10^{-6}$ , which satisfies both requirements of supercriticality and strong rotation. We focus on the differences between the application of no-slip versus stress-free boundary conditions on the horizontal plates. The transition is found at roughly the same parameter values for both boundary conditions, i.e. at 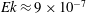$Ek\approx 9\times 10^{-7}$ for 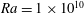$Ra=1\times 10^{10}$ and at 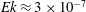$Ek\approx 3\times 10^{-7}$ for 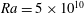$Ra=5\times 10^{10}$ . However, the transition is gradual and it does not exactly coincide in 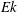$Ek$ for different flow indicators. In particular, we report the characteristics of the transitions in the heat-transfer scaling laws, the boundary-layer thicknesses, the bulk/boundary-layer distribution of dissipations and the mean temperature gradient in the bulk. The flow phenomenology in the geostrophic regime evolves differently for no-slip and stress-free plates. For stress-free conditions, the formation of a large-scale barotropic vortex with associated inverse energy cascade is apparent. For no-slip plates, a turbulent state without large-scale coherent structures is found; the absence of large-scale structure formation is reflected in the energy transfer in the sense that the inverse cascade, present for stress-free boundary conditions, vanishes.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 413 - 432
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Bassom, A. P. & Zhang, K. 1994 Strongly nonlinear convection cells in a rapidly rotating fluid layer. Geophys. Astrophys. Fluid Dyn. 76, 223–238.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Int. 201, 1–17.Google Scholar
Clune, T. & Knobloch, E. 1993 Pattern selection in rotating convection with experimental boundary conditions. Phys. Rev. E 47, 2536–2550.Google Scholar
Dawes, J. H. P. 2001 Rapidly rotating thermal convection at low Prandtl number. J. Fluid Mech. 428, 61–80.Google Scholar
Ecke, R. E. 2015 Scaling of heat transport near onset in rapidly rotating convection. Phys. Lett. A 379, 2221–2223.Google Scholar
Ecke, R. E. & Niemela, J. J. 2014 Heat transport in the geostrophic regime of rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 113, 114301.Google Scholar
Favier, B., Silvers, L. J. & Proctor, M. R. E. 2014 Inverse cascade and symmetry breaking in rapidly rotating Boussinesq convection. Phys. Fluids 26, 096605.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Grooms, I., Julien, K., Weiss, J. B. & Knobloch, E. 2010 Model of convective Taylor columns in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 224501.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.CrossRefGoogle Scholar
Guervilly, C., Hughes, D. W. & Jones, C. A. 2014 Large-scale vortices in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 758, 407–435.CrossRefGoogle Scholar
Heard, W. B. & Veronis, G. 1971 Asymptotic treatment of the stability of a rotating layer of fluid with rigid boundaries. Geophys. Fluid Dyn. 2, 299–316.Google Scholar
Heimpel, M., Aurnou, J. & Wicht, J. 2005 Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 438, 193–196.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2014 Toroidal and poloidal energy in rotating Rayleigh–Bénard convection. J. Fluid Mech. 762, 232–255.Google Scholar
Julien, K., Aurnou, J. M., Calkins, M. A., Knobloch, E., Marti, P., Stellmach, S. & Vasil, G. M. 2016 A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech. 798, 50–87.Google Scholar
Julien, K. & Knobloch, E. 1998 Strongly nonlinear convection cells in a rapidly rotating fluid layer: the tilted f-plane. J. Fluid Mech. 360, 141–178.Google Scholar
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.Google Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012a Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 254503.CrossRefGoogle ScholarPubMed
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012b Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106, 392–428.CrossRefGoogle Scholar
King, E. M. & Aurnou, J. M. 2012 Thermal evidence for Taylor columns in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 85, 016313.CrossRefGoogle ScholarPubMed
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.CrossRefGoogle Scholar
King, E. M., Stellmach, S. & Buffett, B. 2013 Scaling behaviour in Rayleigh–Bénard convection with and without rotation. J. Fluid Mech. 717, 449–471.Google Scholar
King, E. M., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. M. 2009 Boundary layer control of rotating convection systems. Nature 457, 301–304.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2006 Heat flux intensification by vortical flow localization in rotating convection. Phys. Rev. E 74, 056306.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008a Breakdown of large-scale circulation in turbulent rotating convection. Europhys. Lett. 84, 24001.CrossRefGoogle Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008b Enhanced vertical inhomogeneity in turbulent rotating convection. Phys. Rev. Lett. 101, 174501.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2010a Vortex statistics in turbulent rotating convection. Phys. Rev. E 82, 036306.Google Scholar
Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010b Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 642, 445–476.Google Scholar
Kunnen, R. P. J., Corre, Y. & Clercx, H. J. H. 2013 Vortex plume distribution in confined turbulent rotating convection. Eur. Phys. Lett. 104, 54002.Google Scholar
Kunnen, R. P. J., Stevens, R. J. A. M., Overkamp, J., Sun, C., van Heijst, G. J. F. & Clercx, H. J. H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.CrossRefGoogle Scholar
Liu, Y. & Ecke, R. E. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79, 2257–2260.CrossRefGoogle Scholar
Liu, Y. & Ecke, R. E. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80, 036314.Google Scholar
Liu, Y. & Ecke, R. E. 2011 Local temperature measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 84, 016311.Google Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory, and models. Rev. Geophys. 37, 1–64.Google Scholar
Miesch, M. S. 2000 The coupling of solar convection and rotation. Solar Phys. 192, 59–89.Google Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2009 Scale interactions and scaling laws in rotating flows at moderate Rossby numbers and large Reynolds numbers. Phys. Fluids 21, 015108.Google Scholar
Nakagawa, Y. & Frenzen, P. 1955 A theoretical and experimental study of cellular convection in rotating fluids. Tellus 7, 1–21.Google Scholar
Niiler, P. P. & Bisshopp, F. E. 1965 On the influence of Coriolis forces on onset of thermal convection. J. Fluid Mech. 22, 753–761.Google Scholar
Portegies, J. W., Kunnen, R. P. J., van Heijst, G. J. F. & Molenaar, J. 2008 A model for vortical plumes in rotating convection. Phys. Fluids 20, 066602.CrossRefGoogle Scholar
Roberts, P. & Glatzmaier, G. 2000 Geodynamo theory and simulations. Rev. Mod. Phys. 72, 1081–1123.CrossRefGoogle Scholar
Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36, 309–335.Google Scholar
Rubio, A. M., Julien, K., Knobloch, E. & Weiss, J. B. 2014 Upscale energy transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 112, 144501.Google Scholar
Sakai, S. 1997 The horizontal scale of rotating convection in the geostrophic regime. J. Fluid Mech. 333, 85–95.Google Scholar
Schmitz, S. & Tilgner, A. 2009 Heat transport in rotating convection without Ekman layers. Phys. Rev. E 80, 015305(R).Google Scholar
Schmitz, S. & Tilgner, A. 2010 Transitions in turbulent rotating Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 104, 481–489.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650–3653.Google Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113, 254501.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010 Optimal Prandtl number for heat transfer in rotating Rayleigh–Bénard convection. New J. Phys. 12, 075005.CrossRefGoogle Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2012 Breakdown of the large-scale circulation in 𝛤 = 1/2 rotating Rayleigh–Bénard flow. Phys. Rev. E 86, 056311.CrossRefGoogle ScholarPubMed
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2013a Heat transport and flow structure in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 40, 41–49.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013b The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Ahlers, G. & Lohse, D. 2009 Transitions between turbulent states in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 024503.Google Scholar
Veronis, G. 1968 Large-amplitude Bénard convection in a rotating fluid. J. Fluid Mech. 31, 113–139.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Vorobieff, P. & Ecke, R. E. 2002 Turbulent rotating convection: an experimental study. J. Fluid Mech. 458, 191–218.CrossRefGoogle Scholar
Weiss, S. & Ahlers, G. 2011a Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio. J. Fluid Mech. 684, 407–426.Google Scholar
Weiss, S. & Ahlers, G. 2011b The large-scale flow structure in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 461–492.CrossRefGoogle Scholar
Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.CrossRefGoogle ScholarPubMed
Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech. 249, 135–159.Google Scholar
Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.Google Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google ScholarPubMed