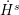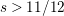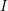Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goyal, Prashant
2022.
Global attractor for weakly damped, forced mKdV equation in low regularity spaces.
São Paulo Journal of Mathematical Sciences,
Vol. 16,
Issue. 2,
p.
1007.
McConnell, Ryan
2023.
Global attractor for the periodic generalized Korteweg-De Vries equation through smoothing.
Discrete and Continuous Dynamical Systems - B,
Vol. 28,
Issue. 2,
p.
1133.
Wang, Ming
2024.
Well Posedness and Global Attractors for the 3D Periodic BBM Equation Below the Energy Space.
Journal of Dynamics and Differential Equations,
Vol. 36,
Issue. 4,
p.
3599.