Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Byun, Sun‐Sig
and
Softova, Lubomira G.
2015.
Gradient estimates in generalized Morrey spaces for parabolic operators.
Mathematische Nachrichten,
Vol. 288,
Issue. 14-15,
p.
1602.
Guliyev, Vagif S.
and
Omarova, Mehriban N.
2016.
Parabolic oblique derivative problem with discontinuous coefficients in generalized weighted Morrey spaces.
Open Mathematics,
Vol. 14,
Issue. 1,
p.
49.
Guliyev, Vagif
Muradova, Shamsiyya
Omarova, Mehriban
and
Softova, Lubomira
2016.
Gradient estimates for parabolic equations in generalized weighted Morrey spaces.
Acta Mathematica Sinica, English Series,
Vol. 32,
Issue. 8,
p.
911.
Akbulut, Ali
and
Hasanov, Amil
2016.
Fractional multilinear integrals with rough kernels on generalized weighted Morrey spaces.
Open Mathematics,
Vol. 14,
Issue. 1,
p.
1023.
Guliyev, Vagif S.
and
Omarova, Mehriban N.
2016.
Corrigendum to: parabolic oblique derivative problem with discontinuous coefficients in generalized weighted Morrey spaces.
Open Mathematics,
Vol. 14,
Issue. 1,
p.
283.
Guliyev, Vagif Sabir
Gadjiev, Tahir
and
Galandarova, Shahla
2017.
Dirichlet boundary value problems for uniformly elliptic equations in modified local generalized Sobolev–Morrey spaces.
Electronic Journal of Qualitative Theory of Differential Equations,
p.
1.
Ruzhansky, Michael
Suragan, Durvudkhan
and
Yessirkegenov, Nurgissa
2018.
Hardy-Littlewood, Bessel-Riesz, and Fractional Integral Operators in Anisotropic Morrey and Campanato Spaces.
Fractional Calculus and Applied Analysis,
Vol. 21,
Issue. 3,
p.
577.
Omarova, M. N.
2020.
Characterizations for the commutator of parabolic nonsingular integral operator on parabolic generalized Orlicz-Morrey spaces.
Tbilisi Mathematical Journal,
Vol. 13,
Issue. 1,
Guliyev, Vagif
Ekincioglu, Ismail
Ahmadli, Aysel
and
Omarova, Mehriban
2020.
Global regularity in Orlicz–Morrey spaces of solutions to parabolic equations with VMO coefficients.
Journal of Pseudo-Differential Operators and Applications,
Vol. 11,
Issue. 4,
p.
1963.
Gadjiev, Tair
and
Suleymanova, Konul
2021.
Recent Developments in the Solution of Nonlinear Differential Equations.
Ho, Kwok-Pun
2022.
Gradient estimates of parabolic Cauchy–Dirichlet problems on Morrey–Banach spaces.
Journal of Elliptic and Parabolic Equations,
Vol. 8,
Issue. 2,
p.
743.
Avsar, Cahit
Aykol, Canay
Hasanov, Javanshir J.
and
Musayev, Ali M.
2023.
Two-weight inequalities for Riesz potential and its commutators on weighted global Morrey-type spaces Gℳωp,θ,φ(ℝn).
Advanced Studies: Euro-Tbilisi Mathematical Journal,
Vol. 16,
Issue. 1,
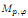 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global 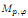 -regularity result for the Cauchy—Dirichlet problem for linear uniformly parabolic equations with vanishing mean oscillation (VMO) coefficients.
-regularity result for the Cauchy—Dirichlet problem for linear uniformly parabolic equations with vanishing mean oscillation (VMO) coefficients.



