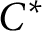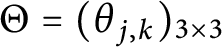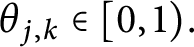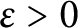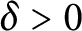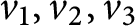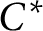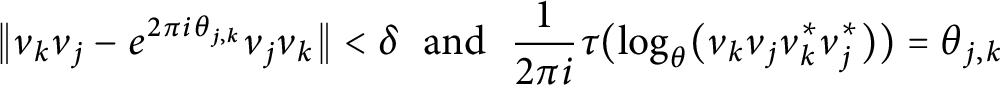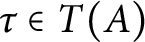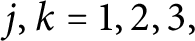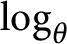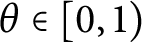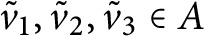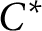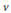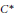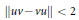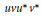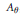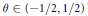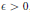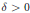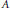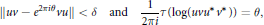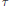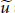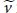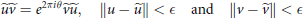We show that if 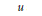 $u$ and
$u$ and 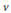 $v$ are any two unitaries in a unital
$v$ are any two unitaries in a unital 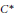 ${{C}^{*}}$–algebra such that
${{C}^{*}}$–algebra such that 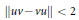 $\left\| uv\,-\,vu \right\|\,<\,2$ and
$\left\| uv\,-\,vu \right\|\,<\,2$ and 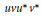 $uv{{u}^{*}}{{v}^{*}}$ commutes with
$uv{{u}^{*}}{{v}^{*}}$ commutes with 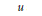 $u$ and
$u$ and 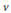 $v$, then the
$v$, then the 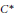 ${{C}^{*}}$–subalgebra
${{C}^{*}}$–subalgebra  ${{A}_{u,v}}$ generated by
${{A}_{u,v}}$ generated by 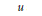 $u$ and
$u$ and 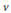 $v$ is isomorphic to a quotient of some rotation algebra
$v$ is isomorphic to a quotient of some rotation algebra 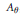 ${{A}_{\theta }}$, provided that
${{A}_{\theta }}$, provided that  ${{A}_{u,v}}$ has a unique tracial state. We also show that the Exel trace formula holds in any unital
${{A}_{u,v}}$ has a unique tracial state. We also show that the Exel trace formula holds in any unital 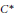 ${{C}^{*}}$–algebra. Let
${{C}^{*}}$–algebra. Let 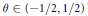 $\theta \,\in \,\left( -1/2,\,1/2 \right)$ be a real number. For any
$\theta \,\in \,\left( -1/2,\,1/2 \right)$ be a real number. For any 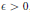 $\in \,>\,0$, we prove that there exists
$\in \,>\,0$, we prove that there exists 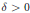 $\delta \,>\,0$ satisfying the following: if
$\delta \,>\,0$ satisfying the following: if 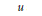 $u$ and
$u$ and 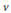 $v$ are two unitaries in any unital simple
$v$ are two unitaries in any unital simple 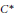 ${{C}^{*}}$–algebra
${{C}^{*}}$–algebra  $A$ with tracial rank zero such that
$A$ with tracial rank zero such that
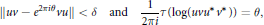 $$\left\| uv\,-\,{{e}^{2\pi i\theta }}vu \right\|\,<\,\delta \,\,\,\text{and}\,\,\frac{1}{2\pi i}\tau \left( \log \left( uv{{u}^{*}}{{v}^{*}} \right) \right)\,=\,\theta ,$$
$$\left\| uv\,-\,{{e}^{2\pi i\theta }}vu \right\|\,<\,\delta \,\,\,\text{and}\,\,\frac{1}{2\pi i}\tau \left( \log \left( uv{{u}^{*}}{{v}^{*}} \right) \right)\,=\,\theta ,$$
for all tracial states  $\tau$ of
$\tau$ of  $A$, then there exists a pair of unitaries
$A$, then there exists a pair of unitaries 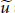 $\widetilde{u}$ and
$\widetilde{u}$ and 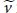 $\widetilde{v}$ in
$\widetilde{v}$ in 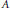 $A$ such that
$A$ such that
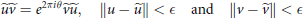 $$\widetilde{u}\widetilde{v}\,=\,{{e}^{2\pi i\theta }}\widetilde{v}\widetilde{u},\,\,\,\,\,\,\,\left\| u\,-\,\widetilde{u} \right\|\,<\,\in \,\,\,\text{and}\,\,\left\| v\,-\,\widetilde{v} \right\|\,<\,\in.$$
$$\widetilde{u}\widetilde{v}\,=\,{{e}^{2\pi i\theta }}\widetilde{v}\widetilde{u},\,\,\,\,\,\,\,\left\| u\,-\,\widetilde{u} \right\|\,<\,\in \,\,\,\text{and}\,\,\left\| v\,-\,\widetilde{v} \right\|\,<\,\in.$$
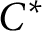 $C^*$
-algebras
$C^*$
-algebras