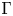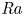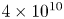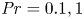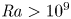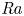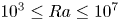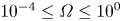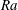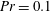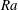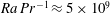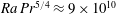4 results
Nonlinear elasticity with vanishing nonlocal self-repulsion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 September 2023, pp. 1-18
-
- Article
- Export citation
Flow states and heat transport in Rayleigh–Bénard convection with different sidewall boundary conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 936 / 10 April 2022
- Published online by Cambridge University Press:
- 18 February 2022, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generation of zonal flows in convective systems by travelling thermal waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 913 / 25 April 2021
- Published online by Cambridge University Press:
- 23 February 2021, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classical and symmetrical horizontal convection: detaching plumes and oscillations
-
- Journal:
- Journal of Fluid Mechanics / Volume 892 / 10 June 2020
- Published online by Cambridge University Press:
- 01 April 2020, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation