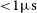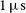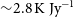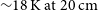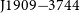94 results
P63: Best Practice Guidance on Human Interaction with Technology in Dementia Update June 2023 – Recommendations from the INDUCT and DISTINCT Networks
-
- Journal:
- International Psychogeriatrics / Volume 35 / Issue S1 / December 2023
- Published online by Cambridge University Press:
- 02 February 2024, pp. 158-159
-
- Article
-
- You have access
- Export citation
The Southern-sky MWA Rapid Two-metre (SMART) pulsar survey—II. Survey status, pulsar census, and first pulsar discoveries – ADDENDUM
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 40 / 2023
- Published online by Cambridge University Press:
- 18 July 2023, e031
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Southern-sky MWA Rapid Two-metre (SMART) pulsar survey—II. Survey status, pulsar census, and first pulsar discoveries
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 40 / 2023
- Published online by Cambridge University Press:
- 11 April 2023, e020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Southern-sky MWA Rapid Two-metre (SMART) pulsar survey—I. Survey design and processing pipeline
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 40 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automated mobile virtual reality cognitive behavior therapy for aviophobia in a natural setting: a randomized controlled trial
-
- Journal:
- Psychological Medicine / Volume 53 / Issue 13 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 6232-6241
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The MeerTime Pulsar Timing Array: A census of emission properties and timing potential
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 39 / 2022
- Published online by Cambridge University Press:
- 18 July 2022, e027
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
343 - Best Practice Guidance on Human Interaction with Technology in Dementia – Recommendations from the INDUCT Network
-
- Journal:
- International Psychogeriatrics / Volume 32 / Issue S1 / October 2020
- Published online by Cambridge University Press:
- 04 November 2020, p. 103
-
- Article
-
- You have access
- Export citation
The MeerKAT telescope as a pulsar facility: System verification and early science results from MeerTime
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 37 / 2020
- Published online by Cambridge University Press:
- 15 July 2020, e028
-
- Article
-
- You have access
- HTML
- Export citation
The Parkes Pulsar Timing Array project: second data release
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 37 / 2020
- Published online by Cambridge University Press:
- 05 June 2020, e020
-
- Article
-
- You have access
- HTML
- Export citation
PW01-200 - Ethnic Differences And Similarities In Treatment Of Common Mental Disorders In Primary And Outpatient Mental Health Care In The Netherlands
-
- Journal:
- European Psychiatry / Volume 25 / Issue S1 / 2010
- Published online by Cambridge University Press:
- 17 April 2020, 25-E1607
-
- Article
-
- You have access
- Export citation
Problem solving therapies for depression: A meta-analysis
-
- Journal:
- European Psychiatry / Volume 22 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 16 April 2020, pp. 9-15
-
- Article
- Export citation
An ultra-wide bandwidth (704 to 4 032 MHz) receiver for the Parkes radio telescope
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 37 / 2020
- Published online by Cambridge University Press:
- 08 April 2020, e012
-
- Article
-
- You have access
- HTML
- Export citation
Does online insomnia treatment reduce depressive symptoms? A randomized controlled trial in individuals with both insomnia and depressive symptoms
-
- Journal:
- Psychological Medicine / Volume 49 / Issue 3 / February 2019
- Published online by Cambridge University Press:
- 11 May 2018, pp. 501-509
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The effects of psychotherapy for depression on anxiety symptoms: a meta-analysis
-
- Journal:
- Psychological Medicine / Volume 48 / Issue 13 / October 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 2140-2152
-
- Article
- Export citation
Polarization study of the pulsars in the globular cluster 47 Tucanae
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 13 / Issue S337 / September 2017
- Published online by Cambridge University Press:
- 04 June 2018, pp. 295-298
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
First interferometric detections of Fast Radio Bursts
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 13 / Issue S337 / September 2017
- Published online by Cambridge University Press:
- 04 June 2018, pp. 322-323
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Pulsar Searches with the SKA
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 13 / Issue S337 / September 2017
- Published online by Cambridge University Press:
- 04 June 2018, pp. 171-174
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Strong field tests of gravity with PSR J1141–6545
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 13 / Issue S337 / September 2017
- Published online by Cambridge University Press:
- 04 June 2018, pp. 142-145
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
High added value of a population-based participatory surveillance system for community acute gastrointestinal, respiratory and influenza-like illnesses in Sweden, 2013–2014 using the web
-
- Journal:
- Epidemiology & Infection / Volume 145 / Issue 6 / April 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1193-1202
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Does Internet-based guided-self-help for depression cause harm? An individual participant data meta-analysis on deterioration rates and its moderators in randomized controlled trials
-
- Journal:
- Psychological Medicine / Volume 46 / Issue 13 / October 2016
- Published online by Cambridge University Press:
- 20 September 2016, pp. 2679-2693
-
- Article
-
- You have access
- HTML
- Export citation