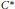11 results
Morpho-functional Analysis of the Head Glands in Three Auchenorrhyncha Species and Their Possible Biological Significance
- Part of
-
- Journal:
- Microscopy and Microanalysis / Volume 28 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 12 September 2022, pp. 2177-2187
- Print publication:
- December 2022
-
- Article
- Export citation
Nanostructure morphology influences in electrical properties of titanium dioxide thin films
-
- Journal:
- Journal of Materials Research / Volume 35 / Issue 21 / 16 November 2020
- Published online by Cambridge University Press:
- 26 August 2020, pp. 3012-3020
- Print publication:
- 16 November 2020
-
- Article
- Export citation
On conjugacy of maximal abelian subalgebras and the outer automorphism group of the Cuntz algebra
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 269-279
- Print publication:
- April 2015
-
- Article
- Export citation
On maximal ideals in certain reduced twisted C*-crossed products
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 158 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 04 February 2015, pp. 399-417
- Print publication:
- May 2015
-
- Article
- Export citation
Vitamins in the treatment of chronic viral hepatitis
-
- Journal:
- British Journal of Nutrition / Volume 105 / Issue 7 / 14 April 2011
- Published online by Cambridge University Press:
- 24 January 2011, pp. 982-989
- Print publication:
- 14 April 2011
-
- Article
-
- You have access
- HTML
- Export citation
AUTOMORPHISMS OF THE UHF ALGEBRA THAT DO NOT EXTEND TO THE CUNTZ ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 07 February 2011, pp. 309-315
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
More localized automorphisms of the Cuntz algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 05 August 2010, pp. 619-631
-
- Article
-
- You have access
- Export citation
On Amenability and Co-Amenability of Algebraic Quantum Groups and Their Corepresentations
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 1 / 01 February 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-60
- Print publication:
- 01 February 2005
-
- Article
-
- You have access
- Export citation
Asymptotic invariance, amenability and generalized Cuntz algebras
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 23 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 23 September 2003, pp. 1323-1346
- Print publication:
- October 2003
-
- Article
- Export citation
COVARIANT REPRESENTATIONS FOR COACTIONS OF HOPF ${\rm C}^*$-ALGEBRAS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 20 March 2003, pp. 209-217
- Print publication:
- March 2003
-
- Article
- Export citation



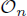 . In particular, we exhibit an uncountable family of maximal abelian subalgebras, conjugate to the standard maximal abelian subalgebra
. In particular, we exhibit an uncountable family of maximal abelian subalgebras, conjugate to the standard maximal abelian subalgebra 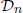 via Bogolubov automorphisms, that are not inner conjugate to
via Bogolubov automorphisms, that are not inner conjugate to 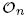 corresponding to permutation matrices in
corresponding to permutation matrices in 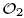 using labelled rooted trees. We also discuss those proper endomorphisms of these Cuntz algebras which restrict to automorphisms of their respective diagonals. In the case of
using labelled rooted trees. We also discuss those proper endomorphisms of these Cuntz algebras which restrict to automorphisms of their respective diagonals. In the case of 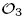 we compute the number of automorphisms of the diagonal induced by permutation matrices in
we compute the number of automorphisms of the diagonal induced by permutation matrices in