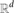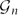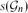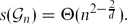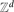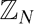Paper
Maximal Empty Boxes Amidst Random Points
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 477-498
-
- Article
- Export citation
Size Ramsey Number of Bounded Degree Graphs for Games
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. 499-516
-
- Article
- Export citation
The Entropy of Random-Free Graphons and Properties
-
- Published online by Cambridge University Press:
- 16 May 2013, pp. 517-526
-
- Article
- Export citation
Expansion in High Dimension for the Growth Constants of Lattice Trees and Lattice Animals
-
- Published online by Cambridge University Press:
- 15 April 2013, pp. 527-565
-
- Article
- Export citation
Lipschitz Functions on Expanders are Typically Flat
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. 566-591
-
- Article
- Export citation
Freiman Homomorphisms of Random Subsets of
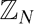 $\mathbb{Z}_{N}$
$\mathbb{Z}_{N}$
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. 592-611
-
- Article
- Export citation
Reimer's Inequality on a Finite Distributive Lattice
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. 612-621
-
- Article
- Export citation
Cross t-Intersecting Integer Sequences from Weighted Erdős–Ko–Rado
-
- Published online by Cambridge University Press:
- 09 May 2013, pp. 622-637
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 22 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 22 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 11 June 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation