10 results
Molecular detection of Trypanosoma spp. and Hepatocystis parasite infections of bats in Northern Nigeria
-
- Journal:
- Parasitology / Volume 149 / Issue 11 / September 2022
- Published online by Cambridge University Press:
- 13 July 2022, pp. 1460-1467
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hepatocystis and Nycteria (Haemosporida) parasite infections of bats in the Central Region of Cameroon
-
- Journal:
- Parasitology / Volume 149 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 51-58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Survey of Hepatocystis parasites of fruit bats in the Amurum forest reserve, Nigeria, identifies first host record for Rousettus aegyptiacus
-
- Journal:
- Parasitology / Volume 146 / Issue 12 / October 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 1550-1554
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hippocampal volume and declarative memory function in combat-related PTSD
-
- Journal:
- Journal of the International Neuropsychological Society / Volume 15 / Issue 6 / November 2009
- Published online by Cambridge University Press:
- 01 November 2009, pp. 830-839
-
- Article
- Export citation
Continuous Self-Maps of the Circle
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 1 / 01 March 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 108-116
- Print publication:
- 01 March 1997
-
- Article
-
- You have access
- Export citation
The Densest Packing of Six Spheres in a Cube
-
- Journal:
- Canadian Mathematical Bulletin / Volume 9 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 20 November 2018, pp. 275-280
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
On the Densest Packing of Spheres in a Cube
-
- Journal:
- Canadian Mathematical Bulletin / Volume 9 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-270
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
The Densest Packing of Five Spheres in a Cube
-
- Journal:
- Canadian Mathematical Bulletin / Volume 9 / Issue 3 / August 1966
- Published online by Cambridge University Press:
- 20 November 2018, pp. 271-274
- Print publication:
- August 1966
-
- Article
-
- You have access
- Export citation
The Densest Packing of 9 Circles in a Square
-
- Journal:
- Canadian Mathematical Bulletin / Volume 8 / Issue 3 / April 1965
- Published online by Cambridge University Press:
- 20 November 2018, pp. 273-277
- Print publication:
- April 1965
-
- Article
-
- You have access
- Export citation
On a Geometric Extremum Problem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 8 / Issue 1 / February 1965
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-27
- Print publication:
- February 1965
-
- Article
-
- You have access
- Export citation

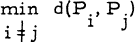 is as large as possible, where d(P
is as large as possible, where d(P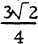 (= m, say), and that 4 it attains this value only if the points form a configuration which is congruent to the one of the points R
(= m, say), and that 4 it attains this value only if the points form a configuration which is congruent to the one of the points R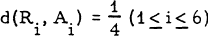 , and so the six points are the vertices of a regular octahedron.
, and so the six points are the vertices of a regular octahedron. is as large as possible, where d(P
is as large as possible, where d(P (=m, say), and if it is equal to m, then the corresponding configuration is congruent to the set of points shown in fig. 1, namely P
(=m, say), and if it is equal to m, then the corresponding configuration is congruent to the set of points shown in fig. 1, namely P