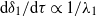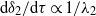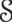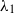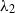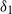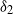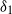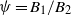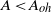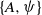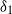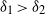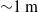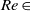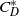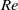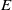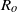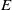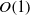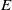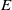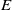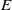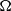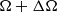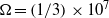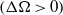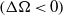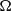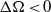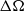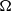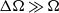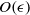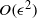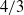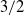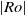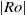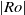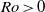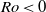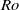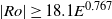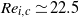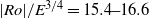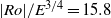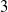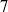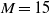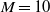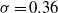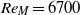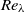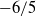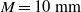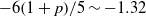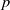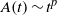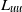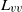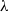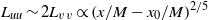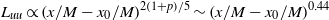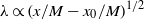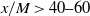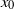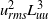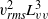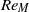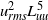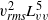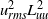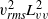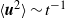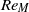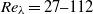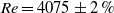Focus on Fluids
Drops sliding down an incline at large contact line velocity: What happens on the road towards rolling?
- Laurent Limat
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 1-4
-
- Article
-
- You have access Access
- Export citation
-
Drops sliding down an incline exhibit fascinating shapes, which indirectly provide a great deal of information about wetting dynamics. Puthenveettil, Kumar & Hopfinger (J. Fluid Mech., vol. 726, 2013, pp. 26–61) have renewed this subject by considering water and mercury drops sliding at high speed. The results raise puzzling questions: how to take into account inertia at a high-speed contact line, large contact angles, the nature of the dissipation at small scale and sliding versus rolling behaviours?
Papers
Control of confined vortex breakdown with partial rotating lids
- L. Mununga, D. Lo Jacono, J. N. Sørensen, T. Leweke, M. C. Thompson, K. Hourigan
-
- Published online by Cambridge University Press:
- 29 November 2013, pp. 5-33
-
- Article
- Export citation
-
Experiments were conducted to determine the effectiveness of controlling vortex breakdown in a confined cylindrical vessel using a small rotating disk, which was flush-mounted into the opposite endwall to the rotating endwall driving the primary recirculating flow. The results show that the control disk, with relatively little power input, can modify the azimuthal and axial flow significantly, changing the entire flow structure in the cylinder. Co-rotation was found to precipitate vortex breakdown onset whereas counter-rotation delays it. Furthermore, for the Reynolds-number range over which breakdown normally exists, co-rotation increases the bubble radial and axial dimensions, while shifting the bubble in the upstream direction. By contrast, counter-rotation tends to reduce the size of the bubble, or completely suppress it, while shifting the bubble in the downstream direction. These effects are amplified substantially by the use of larger control disks and higher rotation ratios. A series of numerical simulations close to the onset Reynolds number reveals that the control disk acts to generate a rotation-rate-invariant local positive or negative azimuthal vorticity source away from the immediate vicinity of the control disk but upstream of breakdown. Advection of this source along streamlines modifies the strength of the azimuthal vorticity ring, which effectively controls whether the flow reverses on the axis, and thus, in turn, whether vortex breakdown occurs. The vorticity source generated by the control disk scales approximately linearly with rotation ratio and cubically with disk diameter; this allows the observed variation of the critical Reynolds number to be approximately predicted.
Transient ventilation dynamics induced by heat sources of unequal strength
- Ajay B. Shrinivas, Gary R. Hunt
-
- Published online by Cambridge University Press:
- 02 December 2013, pp. 34-64
-
- Article
- Export citation
-
We examine theoretically the transient displacement flow and density stratification that develops within a ventilated box after two localized floor-level heat sources of unequal strengths are activated. The heat input is represented by two non-interacting turbulent axisymmetric plumes of constant buoyancy fluxes
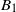 ${B}_{1} $ and
${B}_{1} $ and 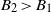 ${B}_{2} \gt {B}_{1} $. The box connects to an unbounded quiescent external environment of uniform density via openings at the top and base. A theoretical model is developed to predict the time evolution of the dimensionless depths
${B}_{2} \gt {B}_{1} $. The box connects to an unbounded quiescent external environment of uniform density via openings at the top and base. A theoretical model is developed to predict the time evolution of the dimensionless depths 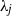 ${\lambda }_{j} $ and mean buoyancies
${\lambda }_{j} $ and mean buoyancies 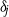 ${\delta }_{j} $ of the ‘intermediate’
${\delta }_{j} $ of the ‘intermediate’ 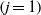 $(j= 1)$ and ‘top’
$(j= 1)$ and ‘top’ 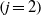 $(j= 2)$ layers leading to steady state. The flow behaviour is classified in terms of a stratification parameter
$(j= 2)$ layers leading to steady state. The flow behaviour is classified in terms of a stratification parameter 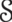 , a dimensionless measure of the relative forcing strengths of the two buoyant layers that drive the flow. We find that
, a dimensionless measure of the relative forcing strengths of the two buoyant layers that drive the flow. We find that 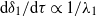 $\mathrm{d} {\delta }_{1} / \mathrm{d} \tau \propto 1/ {\lambda }_{1} $ and
$\mathrm{d} {\delta }_{1} / \mathrm{d} \tau \propto 1/ {\lambda }_{1} $ and 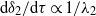 $\mathrm{d} {\delta }_{2} / \mathrm{d} \tau \propto 1/ {\lambda }_{2} $, where
$\mathrm{d} {\delta }_{2} / \mathrm{d} \tau \propto 1/ {\lambda }_{2} $, where  $\tau $ is a dimensionless time. When
$\tau $ is a dimensionless time. When 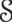
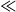 $\hspace{0.167em} \hspace{0.167em} \ll \hspace{0.167em} \hspace{0.167em} $1, the intermediate layer is shallow (small
$\hspace{0.167em} \hspace{0.167em} \ll \hspace{0.167em} \hspace{0.167em} $1, the intermediate layer is shallow (small 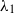 ${\lambda }_{1} $), whereas the top layer is relatively deep (large
${\lambda }_{1} $), whereas the top layer is relatively deep (large 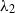 ${\lambda }_{2} $) and, in this limit,
${\lambda }_{2} $) and, in this limit, 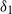 ${\delta }_{1} $ and
${\delta }_{1} $ and 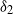 ${\delta }_{2} $ evolve on two characteristically different time scales. This produces a time lag and gives rise to a ‘thermal overshoot’, during which
${\delta }_{2} $ evolve on two characteristically different time scales. This produces a time lag and gives rise to a ‘thermal overshoot’, during which 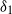 ${\delta }_{1} $ exceeds its steady value and attains a maximum during the transients; a flow feature we refer to, in the context of a ventilated room, as ‘localized overheating’. For a given source strength ratio
${\delta }_{1} $ exceeds its steady value and attains a maximum during the transients; a flow feature we refer to, in the context of a ventilated room, as ‘localized overheating’. For a given source strength ratio 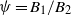 $\psi = {B}_{1} / {B}_{2} $, we show that thermal overshoots are realized for dimensionless opening areas
$\psi = {B}_{1} / {B}_{2} $, we show that thermal overshoots are realized for dimensionless opening areas 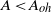 $A\lt {A}_{oh} $ and are strongly dependent on the time history of the flow. We establish the region of
$A\lt {A}_{oh} $ and are strongly dependent on the time history of the flow. We establish the region of 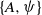 $\{ A, \psi \} $ space where rapid development of
$\{ A, \psi \} $ space where rapid development of 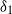 ${\delta }_{1} $ results in
${\delta }_{1} $ results in 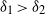 ${\delta }_{1} \gt {\delta }_{2} $, giving rise to a bulk overturning of the buoyant layers. Finally, some implications of these results, specifically to the ventilation of a room, are discussed.
${\delta }_{1} \gt {\delta }_{2} $, giving rise to a bulk overturning of the buoyant layers. Finally, some implications of these results, specifically to the ventilation of a room, are discussed.
Trapped waves on jet currents: asymptotic modal approach
- Victor I. Shrira, Alexey V. Slunyaev
-
- Published online by Cambridge University Press:
- 02 December 2013, pp. 65-104
-
- Article
- Export citation
-
An asymptotic theory of surface waves trapped on vertically uniform jet currents is developed as a first step towards a systematic description of wave dynamics on oceanic jet currents. It has been shown that in a linear setting an asymptotic separation of vertical and horizontal variables, which underpins the modal description of the wave field on currents, is possible if either the current velocity is small compared to the wave celerity or the current width is large compared to the wavelength along the current. The scheme developed enables us to obtain solutions as an asymptotic series with any desired accuracy. The initially three-dimensional problem is reduced to solving one-dimensional equations with the lateral and vertical dependence being prescribed by the corresponding modal structure. To leading order in current magnitude to wave celerity, the boundary value problem specifying the modes and eigenvalues reduces to classical Sturm–Liouville type based upon the one-dimensional stationary Schrödinger equation. The modes, both trapped and ‘passing-through’, form a complete orthogonal set. This makes the modal description of waves on currents a mathematically attractive alternative to the approaches currently adopted. Properties of trapped eigenmodes and their dispersion relations are examined both for broad currents of arbitrary magnitude, where the modes are not orthogonal, and for weak currents, where the modes are orthogonal. Several model profiles for which nice analytical solutions of the leading-order boundary value problem are known were used to get an insight. The asymptotic solutions proved not only to capture qualitative behaviour well but also to provide a good quantitative description even for unrealistically strong and narrow currents. The results are discussed for various oceanic currents, with particular attention paid to the Agulhas Current, for which specific estimates were derived. For typical dominant wind waves and swell, all oceanic-jet-type currents are weak and, correspondingly, the developed asymptotic scheme based upon one-dimensional stationary Schrödinger equation for modes applies.
Spatial simulation of channel flow instability and control
- Alec Kucala, Sedat Biringen
-
- Published online by Cambridge University Press:
- 04 December 2013, pp. 105-123
-
- Article
- Export citation
-
A direct numerical simulation is performed on the full time-dependent three-dimensional Navier–Stokes equations in a spatially developing plane-channel flow at a Reynolds number of 10 000. Two-dimensional eigenfunctions based on the solution of the Orr–Sommerfeld equation are introduced at the inflow with random noise added to simulate a vibrating ribbon transition experiment. The flow is allowed to choose a natural path to secondary instability, either K-type (after Klebanoff) or H-type (after Herbert), depending on the amplitude of the two-dimensional disturbance. For low-amplitude two-dimensional disturbances (1 % of the centreline velocity), H-type modes are found to dominate, while a doubling of the amplitude (2 % of the centreline velocity) produces a mixed H-type/K-type disturbance field with explosive growth of the secondary modes. In addition, the use of a suction/blowing slot that is phase lagged with respect to a fixed wall pressure signal is demonstrated to significantly reduce the energy in the primary mode owing to the destruction of phase between the streamwise and wall-normal velocity components. The use of forward finite-time Lyapunov exponents to generate Lagrangian coherent structures as a means of flow visualization is also presented, showing qualitative agreement with previous experimental visualizations, and represents a viable means of identifying characteristic vortical flow structures.
Surfactant effect on path instability of a rising bubble
- Yoshiyuki Tagawa, Shu Takagi, Yoichiro Matsumoto
-
- Published online by Cambridge University Press:
- 04 December 2013, pp. 124-142
-
- Article
- Export citation
-
We report results from the first systematic experiments for investigating surfactant effects on path instability of an air bubble rising in quiescent water. The addition of surfactant to a gas–water system causes a non-uniform distribution of surfactant concentration along the bubble surface, resulting in variations in the gas–water boundary condition from zero shear stress to non-zero shear stress due to the Marangoni effect. This leads to retarded surface velocity and ends up with immobilization of the bubble surface with increasing surfactant concentration, where the drag corresponds to that of a solid sphere of the same size. Using two high-speed cameras and vertical traverse systems, we measure three-dimensional trajectories, velocities and aspect ratios of a millimetre-sized bubble simultaneously for
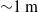 ${\sim }1~\mathrm{m} $. Experimental parameters are the diameter of the bubble and the surfactant concentration of 1-Pentanol or Triton X-100. We explore the surfactant effect on the drag and lift forces acting on the bubble in helical motion. While the drag force monotonically increases with the surfactant concentration as expected, the lift force shows a non-monotonic behaviour. Nevertheless, the direction of the lift force in a reference frame that rotates with the bubble along its trajectory is kept almost constant. We also observe the transient trajectory starting from helical motion to zigzag, which has never been reported in the case of purified water. The instantaneous amplitude and frequency of the transient motion agree with those of the motion regarded as steady. Finally the bubble motions are categorized as straight/helical/zigzag and experimentally examined in the field of two dimensionless numbers: Reynolds number
${\sim }1~\mathrm{m} $. Experimental parameters are the diameter of the bubble and the surfactant concentration of 1-Pentanol or Triton X-100. We explore the surfactant effect on the drag and lift forces acting on the bubble in helical motion. While the drag force monotonically increases with the surfactant concentration as expected, the lift force shows a non-monotonic behaviour. Nevertheless, the direction of the lift force in a reference frame that rotates with the bubble along its trajectory is kept almost constant. We also observe the transient trajectory starting from helical motion to zigzag, which has never been reported in the case of purified water. The instantaneous amplitude and frequency of the transient motion agree with those of the motion regarded as steady. Finally the bubble motions are categorized as straight/helical/zigzag and experimentally examined in the field of two dimensionless numbers: Reynolds number 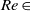 $\mathit{Re}\in $ [300 900] and the normalized drag coefficient
$\mathit{Re}\in $ [300 900] and the normalized drag coefficient 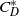 ${ C}_{D}^{\ast } $ which represents the slip condition. Remarkably it is found that the motions of a bubble with the intermediate slip conditions between free-slip and no-slip are helical for a broad range of
${ C}_{D}^{\ast } $ which represents the slip condition. Remarkably it is found that the motions of a bubble with the intermediate slip conditions between free-slip and no-slip are helical for a broad range of 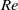 $\mathit{Re}$.
$\mathit{Re}$.
Chaotic advection in a steady, three-dimensional, Ekman-driven eddy
- L. J. Pratt, I. I. Rypina, T. M. Özgökmen, P. Wang, H. Childs, Y. Bebieva
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 143-183
-
- Article
- Export citation
-
We investigate and quantify stirring due to chaotic advection within a steady, three-dimensional, Ekman-driven, rotating cylinder flow. The flow field has vertical overturning and horizontal swirling motion, and is an idealization of motion observed in some ocean eddies. The flow is characterized by strong background rotation, and we explore variations in Ekman and Rossby numbers,
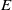 $E$ and
$E$ and 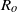 ${R}_{o} $, over ranges appropriate for the ocean mesoscale and submesoscale. A high-resolution spectral element model is used in conjunction with linear analytical theory, weakly nonlinear resonance analysis and a kinematic model in order to map out the barriers, manifolds, resonance layers and other objects that provide a template for chaotic stirring. As expected, chaos arises when a radially symmetric background state is perturbed by a symmetry-breaking disturbance. In the background state, each trajectory lives on a torus and some of the latter survive the perturbation and act as barriers to chaotic transport, a result consistent with an extension of the KAM theorem for three-dimensional, volume-preserving flow. For shallow eddies, where
${R}_{o} $, over ranges appropriate for the ocean mesoscale and submesoscale. A high-resolution spectral element model is used in conjunction with linear analytical theory, weakly nonlinear resonance analysis and a kinematic model in order to map out the barriers, manifolds, resonance layers and other objects that provide a template for chaotic stirring. As expected, chaos arises when a radially symmetric background state is perturbed by a symmetry-breaking disturbance. In the background state, each trajectory lives on a torus and some of the latter survive the perturbation and act as barriers to chaotic transport, a result consistent with an extension of the KAM theorem for three-dimensional, volume-preserving flow. For shallow eddies, where 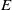 $E$ is
$E$ is 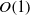 $O(1)$, the flow is dominated by thin resonant layers sandwiched between KAM-type barriers, and the stirring rate is weak. On the other hand, eddies with moderately small
$O(1)$, the flow is dominated by thin resonant layers sandwiched between KAM-type barriers, and the stirring rate is weak. On the other hand, eddies with moderately small 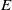 $E$ experience thicker resonant layers, wider-spread chaos and much more rapid stirring. This trend reverses for sufficiently small
$E$ experience thicker resonant layers, wider-spread chaos and much more rapid stirring. This trend reverses for sufficiently small 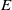 $E$, corresponding to deep eddies, where the vertical rigidity imposed by strong rotation limits the stirring. The bulk stirring rate, estimated from a passive tracer release, confirms the non-monotonic variation in stirring rate with
$E$, corresponding to deep eddies, where the vertical rigidity imposed by strong rotation limits the stirring. The bulk stirring rate, estimated from a passive tracer release, confirms the non-monotonic variation in stirring rate with 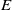 $E$. This result is shown to be consistent with linear Ekman layer theory in conjunction with a resonant width calculation and the Taylor–Proudman theorem. The theory is able to roughly predict the value of
$E$. This result is shown to be consistent with linear Ekman layer theory in conjunction with a resonant width calculation and the Taylor–Proudman theorem. The theory is able to roughly predict the value of 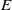 $E$ at which stirring is maximum. For large disturbances, the stirring rate becomes monotonic over the range of Ekman numbers explored. We also explore variation in the eddy aspect ratio.
$E$ at which stirring is maximum. For large disturbances, the stirring rate becomes monotonic over the range of Ekman numbers explored. We also explore variation in the eddy aspect ratio.
Flow instabilities in the wide-gap spherical Couette system
- Johannes Wicht
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 184-221
-
- Article
- Export citation
-
The spherical Couette system is a spherical shell filled with a viscous fluid. Flows are driven by the differential rotation between the inner and the outer boundary that rotate with
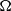 $\Omega $ and
$\Omega $ and 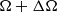 $\Omega + \mathrm{\Delta} \Omega $ about a common axis. This setup has been proposed for second-generation dynamo experiments. We numerically explore the different instabilities emerging for rotation rates up to
$\Omega + \mathrm{\Delta} \Omega $ about a common axis. This setup has been proposed for second-generation dynamo experiments. We numerically explore the different instabilities emerging for rotation rates up to 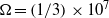 $\Omega = (1/ 3)\times 1{0}^{7} $, venturing also into the nonlinear regime where oscillatory and chaotic solutions are found. The results provide a comprehensive overview of the possible flow regimes. For low values of
$\Omega = (1/ 3)\times 1{0}^{7} $, venturing also into the nonlinear regime where oscillatory and chaotic solutions are found. The results provide a comprehensive overview of the possible flow regimes. For low values of 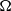 $\Omega $ viscosity dominates and an equatorial jet in meridional circulation and zonal flow develops that becomes unstable as the differential rotation is increased beyond a critical value. For intermediate
$\Omega $ viscosity dominates and an equatorial jet in meridional circulation and zonal flow develops that becomes unstable as the differential rotation is increased beyond a critical value. For intermediate 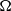 $\Omega $ and an inner boundary rotating slower than the outer one, new double-roll and helical instabilities are found. For large
$\Omega $ and an inner boundary rotating slower than the outer one, new double-roll and helical instabilities are found. For large 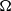 $\Omega $ values Coriolis effects enforce a nearly two-dimensional fundamental flow where a Stewartson shear layer develops at the tangent cylinder. This shear layer is the source of nearly geostrophic non-axisymmetric instabilities that resemble columnar Rossby modes. At first, the instabilities differ significantly depending on whether the inner boundary rotates faster
$\Omega $ values Coriolis effects enforce a nearly two-dimensional fundamental flow where a Stewartson shear layer develops at the tangent cylinder. This shear layer is the source of nearly geostrophic non-axisymmetric instabilities that resemble columnar Rossby modes. At first, the instabilities differ significantly depending on whether the inner boundary rotates faster 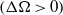 $( \mathrm{\Delta} \Omega \gt 0)$ or slower
$( \mathrm{\Delta} \Omega \gt 0)$ or slower 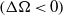 $( \mathrm{\Delta} \Omega \lt 0)$ than the outer one. For very large outer boundary rotation rates, however, both instabilities once more become comparable. Fast inertial waves similar to those observed in recent spherical Couette experiments prevail for larger
$( \mathrm{\Delta} \Omega \lt 0)$ than the outer one. For very large outer boundary rotation rates, however, both instabilities once more become comparable. Fast inertial waves similar to those observed in recent spherical Couette experiments prevail for larger 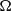 $\Omega $ values and
$\Omega $ values and 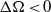 $ \mathrm{\Delta} \Omega \lt 0$ in when
$ \mathrm{\Delta} \Omega \lt 0$ in when 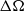 $ \mathrm{\Delta} \Omega $ and
$ \mathrm{\Delta} \Omega $ and 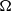 $\Omega $ are of comparable magnitude. For larger differential rotations
$\Omega $ are of comparable magnitude. For larger differential rotations 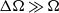 $ \mathrm{\Delta} \Omega \gg \Omega $, however, the equatorial jet instability always takes over.
$ \mathrm{\Delta} \Omega \gg \Omega $, however, the equatorial jet instability always takes over.
Modal stability analysis of a helical vortex tube with axial flow
- Yuji Hattori, Yasuhide Fukumoto
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 222-249
-
- Article
- Export citation
-
The linear stability of a helical vortex tube with axial flow, which is a model of helical vortices emanating from rotating wings, is studied by modal stability analysis. At the leading order the base flow is set to the Rankine vortex with uniform velocity along the helical tube whose centreline is a helix of constant curvature and torsion. The helical vortex tube in an infinite domain, in which the free boundary condition is imposed at the surface of the tube, is our major target although the case of the rigid boundary condition is also considered in order to elucidate the effects of torsion and the combined effects of torsion and axial flow. The analysis is based on the linearized incompressible Euler equations expanded in
 $\epsilon $ which is the ratio of the core to curvature radius of the tube. The unstable growth rate can be evaluated using the leading-order neutral modes called the Kelvin waves with the expanded equations. At
$\epsilon $ which is the ratio of the core to curvature radius of the tube. The unstable growth rate can be evaluated using the leading-order neutral modes called the Kelvin waves with the expanded equations. At 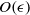 $O(\epsilon )$ the instability is a linear combination of the curvature instability due to the curvature of the tube and the precessional instability due to the axial flow, both parametric instabilities appearing at the same resonance condition. At the next order
$O(\epsilon )$ the instability is a linear combination of the curvature instability due to the curvature of the tube and the precessional instability due to the axial flow, both parametric instabilities appearing at the same resonance condition. At the next order 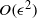 $O({\epsilon }^{2} )$ not only the effects of torsion but also the combined effects of torsion and axial flow appear, a fact which has been shown only for the short-wave limit. The maximum growth rate increases for the right-handed/left-handed helix with positive/negative helicity, in which the torsion makes the period of particle motion increase. All results converge to the previous local stability results in the short-wave limit. The differences between the two cases of different boundary conditions are due to the isolated mode of the free boundary case, whose dispersion curve depends strongly on the axial flow.
$O({\epsilon }^{2} )$ not only the effects of torsion but also the combined effects of torsion and axial flow appear, a fact which has been shown only for the short-wave limit. The maximum growth rate increases for the right-handed/left-handed helix with positive/negative helicity, in which the torsion makes the period of particle motion increase. All results converge to the previous local stability results in the short-wave limit. The differences between the two cases of different boundary conditions are due to the isolated mode of the free boundary case, whose dispersion curve depends strongly on the axial flow.
Scaling the propulsive performance of heaving flexible panels
- Daniel B. Quinn, George V. Lauder, Alexander J. Smits
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 250-267
-
- Article
- Export citation
-
We present an experimental investigation of flexible panels actuated with heave oscillations at their leading edge. Results are presented from kinematic video analysis, particle image velocimetry, and direct force measurements. Both the trailing edge amplitude and the mode shapes of the panel are found to scale with dimensionless parameters originating from the Euler–Bernoulli beam equation. The time-averaged net thrust increases with heaving frequency, but experiences localized boosts near resonant frequencies where the trailing edge amplitude is maximized. These boosts correspond to local maxima in the propulsive efficiency. For a constant heave amplitude, the time-averaged net thrust coefficient is shown to be a function of Strouhal number over a wide range of conditions. It appears, therefore, that self-propelled swimming (zero net thrust) only occurs over a small range of Strouhal numbers. Under these near-constant Strouhal number conditions, the propulsive economy increases with higher flexibilities and slower swimming speeds.
Strong swirl approximation and intensive vortices in the atmosphere
- A. Y. Klimenko
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 268-298
-
- Article
- Export citation
-
This work investigates intensive vortices, which are characterised by the existence of a converging radial flow that significantly intensifies the flow rotation. Evolution and amplification of the vorticity present in the flow play important roles in the formation of the vortex. When rotation in the flow becomes sufficiently strong (this implies the validity of the strong swirl approximation, which has been developed in a series of publications since the 1950s) the previous analysis of the author and the present work determine that further amplification of vorticity is moderated by interactions of vorticity and velocity. This imposes physical constraints on the flow, resulting in the so-called compensating regime, where the radial distribution of the axial vorticity is characterised by the
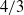 $4/ 3$ and
$4/ 3$ and 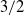 $3/ 2$ power laws. This asymptotic treatment of a strong swirl is based on vorticity equations and involves higher-order terms. This treatment incorporates multi-scale analysis indicating downstream relaxation of the flow to the compensating regime. The present work also investigates and takes into account viscous and transient effects. One of the main points of this work is the applicability of the power laws of the compensating regime to intermediate regions in large atmospheric vortices, such as tropical cyclones and tornadoes.
$3/ 2$ power laws. This asymptotic treatment of a strong swirl is based on vorticity equations and involves higher-order terms. This treatment incorporates multi-scale analysis indicating downstream relaxation of the flow to the compensating regime. The present work also investigates and takes into account viscous and transient effects. One of the main points of this work is the applicability of the power laws of the compensating regime to intermediate regions in large atmospheric vortices, such as tropical cyclones and tornadoes.
Linear stability analysis of a shear layer induced by differential coaxial rotation within a cylindrical enclosure
- Tony Vo, Luca Montabone, Gregory J. Sheard
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 299-334
-
- Article
- Export citation
-
The generation of distinct polygonal configurations via the instability of a Stewartson shear layer is numerically investigated. The shear layer is induced using a rotating cylindrical tank with differentially forced disks located at the top and bottom boundaries. The incompressible Navier–Stokes equations are solved on a two-dimensional semi-meridional plane. Axisymmetric base flows are consistently found to reach a steady state for a wide range of flow conditions, and details of the vertical structure are revealed. An axially invariant two-dimensional flow is ascertained for small
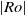 $\vert \mathit{Ro}\vert $, which substantiates the Taylor–Proudman theorem. Sufficient increases in
$\vert \mathit{Ro}\vert $, which substantiates the Taylor–Proudman theorem. Sufficient increases in 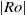 $\vert \mathit{Ro}\vert $ forcing develops flow features that break this quasi-two-dimensionality. The onset of this breaking occurs earlier with increasing
$\vert \mathit{Ro}\vert $ forcing develops flow features that break this quasi-two-dimensionality. The onset of this breaking occurs earlier with increasing 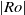 $\vert \mathit{Ro}\vert $ for
$\vert \mathit{Ro}\vert $ for 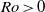 $\mathit{Ro}\gt 0$ compared with
$\mathit{Ro}\gt 0$ compared with 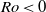 $\mathit{Ro}\lt 0$. The thickness scaling of the vertical Stewartson layers are in agreement with previous analytical results. Growth rates of the most unstable azimuthal wavenumber from a global linear stability analysis are obtained. The threshold between axisymmetric and non-axisymmetric flow follows a power law, and both positive- and negative-
$\mathit{Ro}\lt 0$. The thickness scaling of the vertical Stewartson layers are in agreement with previous analytical results. Growth rates of the most unstable azimuthal wavenumber from a global linear stability analysis are obtained. The threshold between axisymmetric and non-axisymmetric flow follows a power law, and both positive- and negative-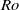 $\mathit{Ro}$ regimes are found to adopt the same threshold for instability, namely
$\mathit{Ro}$ regimes are found to adopt the same threshold for instability, namely 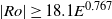 $\vert \mathit{Ro}\vert \geq 18. 1{E}^{0. 767} $. This relationship corresponds to a constant critical internal Reynolds number of
$\vert \mathit{Ro}\vert \geq 18. 1{E}^{0. 767} $. This relationship corresponds to a constant critical internal Reynolds number of 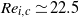 ${\mathit{Re}}_{i, c} \simeq 22. 5$. A review of reported critical internal Reynolds number and their characteristic length scales yields a consistent instability onset given by
${\mathit{Re}}_{i, c} \simeq 22. 5$. A review of reported critical internal Reynolds number and their characteristic length scales yields a consistent instability onset given by 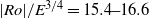 $\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 4{\unicode{x2013}} 16. 6$; here we find
$\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 4{\unicode{x2013}} 16. 6$; here we find 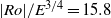 $\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 8$. At the onset of linear instability, the initially circular shear layer deforms, resulting in a polygonal structure consistent with barotropic instability. Dominant azimuthal wavenumbers range from
$\vert \mathit{Ro}\vert / {E}^{3/ 4} = 15. 8$. At the onset of linear instability, the initially circular shear layer deforms, resulting in a polygonal structure consistent with barotropic instability. Dominant azimuthal wavenumbers range from 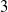 $3$ to
$3$ to 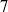 $7$ at the onset of instability for the parameter space explored. Empirical relationships for the preferential wavenumber have been obtained. Additional instability modes have been discovered that favour higher wavenumbers, and these exhibit structures localized to the disk–tank interfaces.
$7$ at the onset of instability for the parameter space explored. Empirical relationships for the preferential wavenumber have been obtained. Additional instability modes have been discovered that favour higher wavenumbers, and these exhibit structures localized to the disk–tank interfaces.
Global stability of stretched jets: conditions for the generation of monodisperse micro-emulsions using coflows
- J. M. Gordillo, A. Sevilla, F. Campo-Cortés
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 335-357
-
- Article
- Export citation
-
In this paper we reveal the physics underlying the conditions needed for the generation of emulsions composed of uniformly sized drops of micrometric or submicrometric diameters when two immiscible streams flow in parallel under the so-called tip streaming regime after Suryo and Basaran (Phys. Fluids, vol. 18, 2006, 082102). Indeed, when inertial effects in both liquid streams are negligible, the inner to outer flow-rate and viscosity ratios are small enough and the capillary number is above an experimentally determined threshold which is predicted by our theoretical results with small relative errors, a steady micrometre-sized jet is issued from the apex of a conical drop. Under these conditions, the jet disintegrates into drops with a very well-defined mean diameter, giving rise to a monodisperse microemulsion. Here, we demonstrate that the regime in which uniformly sized drops are produced corresponds to values of the capillary number for which the cone-jet system is globally stable. Interestingly enough, our general stability theory reveals that liquid jets with a cone-jet structure are much more stable than their cylindrical counterparts thanks, mostly, to a capillary stabilization mechanism described here for the first time. Our findings also limit the validity of the type of stability analysis based on the common parallel flow assumption to only those situations in which the liquid jet diameter is almost constant.
Geostrophic adjustment in a closed basin with islands
- E. R. Johnson, R. H. J. Grimshaw
-
- Published online by Cambridge University Press:
- 05 December 2013, pp. 358-377
-
- Article
- Export citation
-
We consider the geostrophic adjustment of a density-stratified fluid in a basin of constant depth on an
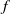 $f$-plane in the context of linearized theory. For a single vertical mode, the equations are equivalent to those for a linearized shallow-water theory for a homogeneous fluid. Associated with any initial state there is a unique steady geostrophically adjusted component of the flow compatible with the initial conditions. This steady component gives the time average of the flow and is analogous to the adjusted flow in an unbounded domain without islands. The remainder of the response consists of superinertial Poincaré and subinertial Kelvin wave modes and expressions for the energy partition between the modes in arbitrary basins again follow directly from the initial conditions. The solution for an arbitrary initial density distribution released from rest in a circular domain is found in closed form. When the Rossby radius is much smaller than the basin radius, appropriate for the baroclinic modes, the interior adjusted solution is close to that of the initial state, except for small-amplitude trapped Poincaré waves, while Kelvin waves propagate around the boundaries, carrying, without change of form, the deviation of the initial height field from its average.
$f$-plane in the context of linearized theory. For a single vertical mode, the equations are equivalent to those for a linearized shallow-water theory for a homogeneous fluid. Associated with any initial state there is a unique steady geostrophically adjusted component of the flow compatible with the initial conditions. This steady component gives the time average of the flow and is analogous to the adjusted flow in an unbounded domain without islands. The remainder of the response consists of superinertial Poincaré and subinertial Kelvin wave modes and expressions for the energy partition between the modes in arbitrary basins again follow directly from the initial conditions. The solution for an arbitrary initial density distribution released from rest in a circular domain is found in closed form. When the Rossby radius is much smaller than the basin radius, appropriate for the baroclinic modes, the interior adjusted solution is close to that of the initial state, except for small-amplitude trapped Poincaré waves, while Kelvin waves propagate around the boundaries, carrying, without change of form, the deviation of the initial height field from its average.
On invariants in grid turbulence at moderate Reynolds numbers
- T. Kitamura, K. Nagata, Y. Sakai, A. Sasoh, O. Terashima, H. Saito, T. Harasaki
-
- Published online by Cambridge University Press:
- 06 December 2013, pp. 378-406
-
- Article
- Export citation
-
The decay characteristics and invariants of grid turbulence were investigated by means of laboratory experiments conducted in a wind tunnel. A turbulence-generating grid was installed at the entrance of the test section for generating nearly isotropic turbulence. Five grids (square bars of mesh sizes
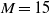 $M= 15$, 25 and 50 mm and cylindrical bars of mesh sizes
$M= 15$, 25 and 50 mm and cylindrical bars of mesh sizes 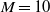 $M= 10$ and 25 mm) were used. The solidity of all grids is
$M= 10$ and 25 mm) were used. The solidity of all grids is 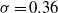 $\sigma = 0. 36$. The instantaneous streamwise and vertical (cross-stream) velocities were measured by hot-wire anemometry. The mesh Reynolds numbers were adjusted to
$\sigma = 0. 36$. The instantaneous streamwise and vertical (cross-stream) velocities were measured by hot-wire anemometry. The mesh Reynolds numbers were adjusted to 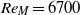 $R{e}_{M} = 6700$, 9600, 16 000 and 33 000. The Reynolds numbers based on the Taylor microscale
$R{e}_{M} = 6700$, 9600, 16 000 and 33 000. The Reynolds numbers based on the Taylor microscale 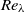 $R{e}_{\lambda } $ in the decay region ranged from 27 to 112. In each case, the result shows that the decay exponent of turbulence intensity is close to the theoretical value of
$R{e}_{\lambda } $ in the decay region ranged from 27 to 112. In each case, the result shows that the decay exponent of turbulence intensity is close to the theoretical value of 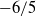 ${- }6/ 5$ (for the
${- }6/ 5$ (for the 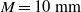 $M= 10~\mathrm{mm} $ grid,
$M= 10~\mathrm{mm} $ grid, 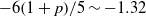 ${- }6(1+ p)/ 5\sim - 1. 32$) for Saffman turbulence. Here,
${- }6(1+ p)/ 5\sim - 1. 32$) for Saffman turbulence. Here, 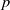 $p$ is the power of the dimensionless energy dissipation coefficient,
$p$ is the power of the dimensionless energy dissipation coefficient, 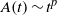 $A(t)\sim {t}^{p} $. Furthermore, each case shows that streamwise variations in the integral length scales,
$A(t)\sim {t}^{p} $. Furthermore, each case shows that streamwise variations in the integral length scales, 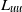 ${L}_{uu} $ and
${L}_{uu} $ and 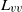 ${L}_{vv} $, and the Taylor microscale
${L}_{vv} $, and the Taylor microscale 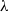 $\lambda $ grow according to
$\lambda $ grow according to 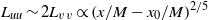 ${L}_{uu} \sim 2{L}_{vv} \propto {(x/ M- {x}_{0} / M)}^{2/ 5} $ (for the
${L}_{uu} \sim 2{L}_{vv} \propto {(x/ M- {x}_{0} / M)}^{2/ 5} $ (for the 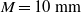 $M= 10~\mathrm{mm} $ grid,
$M= 10~\mathrm{mm} $ grid, 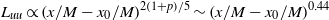 ${L}_{uu} \propto {(x/ M- {x}_{0} / M)}^{2(1+ p)/ 5} \sim {(x/ M- {x}_{0} / M)}^{0. 44} $) and
${L}_{uu} \propto {(x/ M- {x}_{0} / M)}^{2(1+ p)/ 5} \sim {(x/ M- {x}_{0} / M)}^{0. 44} $) and 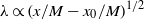 $\lambda \propto {(x/ M- {x}_{0} / M)}^{1/ 2} $, respectively, at
$\lambda \propto {(x/ M- {x}_{0} / M)}^{1/ 2} $, respectively, at 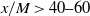 $x/ M\gt 40{\unicode{x2013}} 60$ (depending on the experimental conditions, including grid geometry), where
$x/ M\gt 40{\unicode{x2013}} 60$ (depending on the experimental conditions, including grid geometry), where  $x$ is the streamwise distance from the grid and
$x$ is the streamwise distance from the grid and 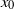 ${x}_{0} $ is the virtual origin. We demonstrated that in the decay region of grid turbulence,
${x}_{0} $ is the virtual origin. We demonstrated that in the decay region of grid turbulence, 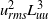 ${ u}_{\mathit{rms}}^{2} { L}_{uu}^{3} $ and
${ u}_{\mathit{rms}}^{2} { L}_{uu}^{3} $ and 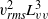 ${ v}_{\mathit{rms}}^{2} { L}_{vv}^{3} $, which correspond to Saffman’s integral, are constant for all grids and examined
${ v}_{\mathit{rms}}^{2} { L}_{vv}^{3} $, which correspond to Saffman’s integral, are constant for all grids and examined 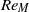 $R{e}_{M} $ values. However,
$R{e}_{M} $ values. However, 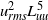 ${ u}_{\mathit{rms}}^{2} { L}_{uu}^{5} $ and
${ u}_{\mathit{rms}}^{2} { L}_{uu}^{5} $ and 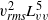 ${ v}_{\mathit{rms}}^{2} { L}_{vv}^{5} $, which correspond to Loitsianskii’s integral, and
${ v}_{\mathit{rms}}^{2} { L}_{vv}^{5} $, which correspond to Loitsianskii’s integral, and 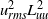 ${ u}_{\mathit{rms}}^{2} { L}_{uu}^{2} $ and
${ u}_{\mathit{rms}}^{2} { L}_{uu}^{2} $ and 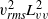 ${ v}_{\mathit{rms}}^{2} { L}_{vv}^{2} $, which correspond to the complete self-similarity of energy spectrum and
${ v}_{\mathit{rms}}^{2} { L}_{vv}^{2} $, which correspond to the complete self-similarity of energy spectrum and 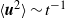 $\langle {\boldsymbol{u}}^{2} \rangle \sim {t}^{- 1} $, are not constant. Consequently, we conclude that grid turbulence is a type of Saffman turbulence for the examined
$\langle {\boldsymbol{u}}^{2} \rangle \sim {t}^{- 1} $, are not constant. Consequently, we conclude that grid turbulence is a type of Saffman turbulence for the examined 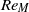 $R{e}_{M} $ range of 6700–33 000 (
$R{e}_{M} $ range of 6700–33 000 (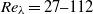 $R{e}_{\lambda } = 27{\unicode{x2013}} 112$) regardless of grid geometry.
$R{e}_{\lambda } = 27{\unicode{x2013}} 112$) regardless of grid geometry.
Arrest of the flow of wet granular matter
- Klaus Roeller, Johannes Blaschke, Stephan Herminghaus, Jürgen Vollmer
-
- Published online by Cambridge University Press:
- 06 December 2013, pp. 407-422
-
- Article
-
- You have access Access
- Open access
- Export citation
-
We study the arrest of three-dimensional flow of wet granular matter subject to a sinusoidal external force and a gravitational field confining the flow in the vertical direction. The minimal strength of the external force that is required to keep the system in motion, i.e. the critical force, is determined by considering the balance of injected and dissipated power. This provides a prediction whose quality is demonstrated by a data collapse for an extensive set of event-driven molecular-dynamics simulations where we varied the system size, particle number, the energy dissipated upon rupturing capillary bridges, and the bridge length at which rupture occurs. The same approach also works for systems that are kept at a fixed density by confining walls. In both cases, this universal method provides the critical force irrespective of the flow profile, and without specifying the hydrodynamic equations.
Flow-induced segregation in confined multicomponent suspensions: effects of particle size and rigidity
- Amit Kumar, Rafael G. Henríquez Rivera, Michael D. Graham
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 423-462
-
- Article
- Export citation
-
The effects of particle size and rigidity on segregation behaviour in confined simple shear flow of binary suspensions of fluid-filled elastic capsules are investigated in a model system that resembles blood. We study this problem with direct simulations as well as with a master equation model that incorporates two key sources of wall-normal particle transport: wall-induced migration and hydrodynamic pair collisions. The simulation results indicate that, in a mixture of large and small particles with equal capillary numbers, the small particles marginate, while the large particles antimarginate in their respective dilute suspensions. Here margination refers to localization of particles near walls, while antimargination refers to the opposite. In a mixture of particles with equal size and unequal capillary number, the stiffer particles marginate while the flexible particles antimarginate. The master equation model traces the origins of the segregation behaviour to the size and rigidity dependence of the wall-induced migration velocity and of the cross-stream particle displacements in various types of collisions. In particular, segregation by rigidity, especially at low volume fractions, is driven in large part by heterogeneous collisions, in which the stiff particle undergoes larger displacement. In contrast, segregation by size is driven mostly by the larger wall-induced migration velocity of larger particles. Additionally, a non-local drift-diffusion equation is derived from the master equation model, which provides further insights into the segregation behaviour.
Experimental investigation of transitional flow in a toroidal pipe
- J. Kühnen, M. Holzner, B. Hof, H. C. Kuhlmann
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 463-491
-
- Article
- Export citation
-
The flow instability and further transition to turbulence in a toroidal pipe (torus) with curvature ratio (tube-to-coiling diameter) 0.049 is investigated experimentally. The flow inside the toroidal pipe is driven by a steel sphere fitted to the inner pipe diameter. The sphere is moved with constant azimuthal velocity from outside the torus by a moving magnet. The experiment is designed to investigate curved pipe flow by optical measurement techniques. Using stereoscopic particle image velocimetry, laser Doppler velocimetry and pressure drop measurements, the flow is measured for Reynolds numbers ranging from 1000 to 15 000. Time- and space-resolved velocity fields are obtained and analysed. The steady axisymmetric basic flow is strongly influenced by centrifugal effects. On an increase of the Reynolds number we find a sequence of bifurcations. For
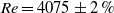 $\mathit{Re}= 4075\pm 2\hspace{0.167em} \% $ a supercritical bifurcation to an oscillatory flow is found in which waves travel in the streamwise direction with a phase velocity slightly faster than the mean flow. The oscillatory flow is superseded by a presumably quasi-periodic flow at a further increase of the Reynolds number before turbulence sets in. The results are found to be compatible, in general, with earlier experimental and numerical investigations on transition to turbulence in helical and curved pipes. However, important aspects of the bifurcation scenario differ considerably.
$\mathit{Re}= 4075\pm 2\hspace{0.167em} \% $ a supercritical bifurcation to an oscillatory flow is found in which waves travel in the streamwise direction with a phase velocity slightly faster than the mean flow. The oscillatory flow is superseded by a presumably quasi-periodic flow at a further increase of the Reynolds number before turbulence sets in. The results are found to be compatible, in general, with earlier experimental and numerical investigations on transition to turbulence in helical and curved pipes. However, important aspects of the bifurcation scenario differ considerably.
Approximate modelling of the leftward flow and morphogen transport in the embryonic node by specifying vorticity at the ciliated surface
- A. V. Kuznetsov, D. G. Blinov, A. A. Avramenko, I. V. Shevchuk, A. I. Tyrinov, I. A. Kuznetsov
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 492-521
-
- Article
- Export citation
-
In this paper, we have developed an approximate method for modelling the flow of embryonic fluid in a ventral node. We simplified the problem as flow in a two-dimensional cavity; the effect of rotating cilia was modelled by specifying a constant vorticity at the edge of the ciliated layer. We also developed an approximate solution for morphogen transport in the nodal pit. The solutions were obtained utilizing the proper generalized decomposition (PGD) method. We compared our approximate solutions with the results of numerical simulation of flow caused by the rotation of 81 cilia, and obtained reasonable agreement in most of the flow domain. We discuss locations where agreement is less accurate. The obtained semi-analytical solutions simplify the analysis of flow and morphogen distribution in a nodal pit.
Bioconvection under uniform shear: linear stability analysis
- Yongyun Hwang, T. J. Pedley
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. 522-562
-
- Article
- Export citation
-
The role of uniform shear in bioconvective instability in a shallow suspension of swimming gyrotactic cells is studied using linear stability analysis. The shear is introduced by applying a plane Couette flow, and it significantly disturbs gravitaxis of the cell. The unstably stratified basic state of the cell concentration is gradually relieved as the shear rate is increased, and it even becomes stably stratified at very large shear rates. Stability of the basic state is significantly changed. The instability at high wavenumbers is drastically damped out with the shear rate, while that at low wavenumbers is destabilized. However, at very large shear rates, the latter is also suppressed. The most unstable mode is found as a pair of streamwise uniform rolls aligned with the shear, analogous to Rayleigh–Bénard convection in plane Couette flow. To understand these findings, the physical mechanism of the bioconvective instability is reexamined with several sets of numerical experiments. It is shown that the bioconvective instability in a shallow suspension originates from three different physical processes: gravitational overturning, gyrotaxis of the cell and negative cross-diffusion flux. The first mechanism is found to rule the behaviour of low-wavenumber instability whereas the last two mechanisms are mainly associated with high-wavenumber instability. With the increase of the shear rate, the former is enhanced, thereby leading to destabilization at low wavenumbers, whereas the latter two mechanisms are significantly suppressed. For streamwise varying perturbations, shear with sufficiently large rates is also found to play a stabilizing role as in Rayleigh–Bénard convection. However, at small shear rates, it destabilizes these perturbations through the mechanism of overstability discussed by Hill, Pedley and Kessler (J. Fluid Mech., vol. 208, 1989, pp. 509–543). Finally, the present findings are compared with a recent experiment by Croze, Ashraf and Bees (Phys. Biol., vol. 7, 2010, 046001) and they are in qualitative agreement.


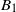
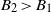
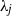
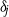
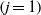
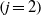
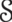 , a dimensionless measure of the relative forcing strengths of the two buoyant layers that drive the flow. We find that
, a dimensionless measure of the relative forcing strengths of the two buoyant layers that drive the flow. We find that