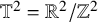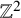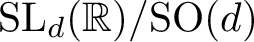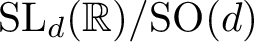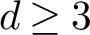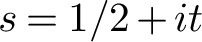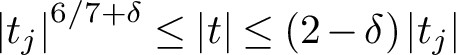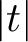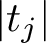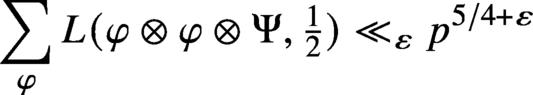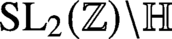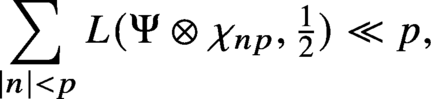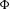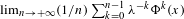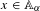Refine search
Actions for selected content:
8 results
TRACE FORMULAS IN NONCOMMUTATIVE GEOMETRY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Gaussian fluctuations in the equipartition principle for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 August 2023, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Superscars for arithmetic point scatters II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 May 2023, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTUM ERGODICITY FOR COMPACT QUOTIENTS OF
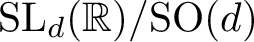 $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 2075-2115
- Print publication:
- September 2023
-
- Article
- Export citation
MOMENTS AND HYBRID SUBCONVEXITY FOR SYMMETRIC-SQUARE L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 2029-2073
- Print publication:
- September 2023
-
- Article
- Export citation
Bounds for twisted symmetric square L-functions via half-integral weight periods
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e44
-
- Article
-
- You have access
- Open access
- Export citation
Ergodic properties of the Anzai skew-product for the non-commutative torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 January 2020, pp. 1064-1085
- Print publication:
- April 2021
-
- Article
- Export citation
PERTURBATION OF THE SEMICLASSICAL SCHRÖDINGER EQUATION ON NEGATIVELY CURVED SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 27 August 2015, pp. 787-835
- Print publication:
- September 2017
-
- Article
- Export citation