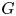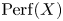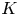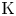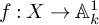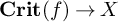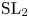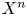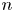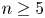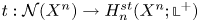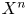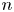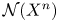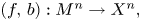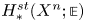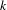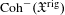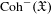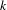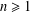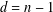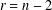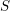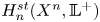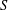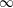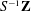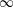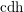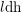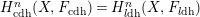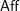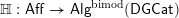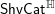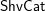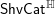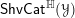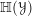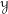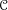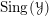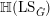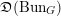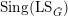39 results in 18Fxx
Dirac geometry II: coherent cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 February 2024, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categories of graphs for operadic structures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 155-212
- Print publication:
- January 2024
-
- Article
- Export citation
On distributivity in higher algebra I: the universal property of bispans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2326-2415
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The localisation theorem for the K-theory of stable ∞-categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 July 2023, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gabber rigidity in hermitian K-theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 April 2023, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISATIONS OF LODAY’S ASSEMBLY MAPS FOR LAWVERE’S ALGEBRAIC THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 811-837
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 August 2022, pp. 311-345
- Print publication:
- January 2024
-
- Article
- Export citation
The equivalence between rational G-sheaves and rational G-Mackey functors for profinite G
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 345-368
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Monoidal abelian envelopes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 1584-1609
- Print publication:
- July 2021
-
- Article
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
CATEGORICAL SEMANTICS OF METRIC SPACES AND CONTINUOUS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1044-1078
- Print publication:
- September 2020
-
- Article
- Export citation
DERIVED NON-ARCHIMEDEAN ANALYTIC HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 August 2020, pp. 335-366
- Print publication:
- January 2022
-
- Article
- Export citation
RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 April 2020, pp. 115-144
- Print publication:
- February 2022
-
- Article
- Export citation
Projective objects and the modified trace in factorisable finite tensor categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 26 March 2020, pp. 770-821
- Print publication:
- April 2020
-
- Article
- Export citation
On Steenrod 𝕃-homology, generalized manifolds, and surgery
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 March 2020, pp. 579-607
-
- Article
- Export citation
CATEGORIFYING RATIONALIZATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 09 January 2020, e42
-
- Article
-
- You have access
- Open access
- Export citation
A BETTER COMPARISON OF
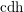 $\operatorname{cdh}$- AND
$\operatorname{cdh}$- AND 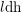 $l\operatorname{dh}$-COHOMOLOGIES
$l\operatorname{dh}$-COHOMOLOGIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 13 September 2019, pp. 183-213
- Print publication:
- December 2019
-
- Article
- Export citation
Sheaves of categories with local actions of Hochschild cochains
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1521-1567
- Print publication:
- August 2019
-
- Article
- Export citation
Grothendieck Ring of Varieties with Actions of Finite Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 08 March 2019, pp. 925-948
-
- Article
- Export citation