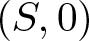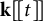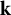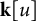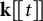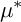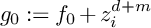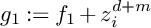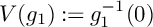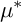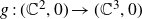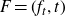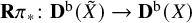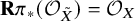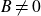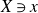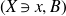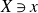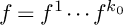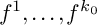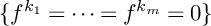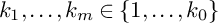71 results
Equisingularity in pencils of curves on germs of reduced complex surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 June 2024, pp. 1-23
-
- Article
- Export citation
Strict positivity of Kähler–Einstein currents
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-15
-
- Article
- Export citation
Convexity of multiplicities of filtrations on local rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 878-914
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bound of the number of weighted blow-ups to compute the minimal log discrepancy for smooth 3-folds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 495-515
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to determine a curve singularity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 January 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 05 December 2023, pp. 488-497
- Print publication:
- June 2024
-
- Article
- Export citation
On the topology of the transversal slice of a quasi-homogeneous map germ
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 339-359
- Print publication:
- March 2024
-
- Article
- Export citation
Homological Bondal-Orlov localization conjecture for rational singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Łojasiewicz exponent of nondegenerate surface singularities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1391-1410
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of Log Terminal and Semi Log Canonical Singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Divisors computing minimal log discrepancies on lc surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 107-128
- Print publication:
- July 2023
-
- Article
- Export citation
On parabolic subgroups of symplectic reflection groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 401-413
- Print publication:
- May 2023
-
- Article
- Export citation
Lower bounds on Hilbert–Kunz multiplicities and maximal F-signatures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 December 2022, pp. 247-271
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG COHEN–MACAULAY TEST IDEALS IN EQUAL CHARACTERISTIC ZERO VIA ULTRAPRODUCTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 07 December 2022, pp. 549-575
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE MILNOR FIBRATION OF CERTAIN NEWTON DEGENERATE FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 410-433
- Print publication:
- June 2023
-
- Article
- Export citation
ANALYTIC SPREAD OF FILTRATIONS ON TWO-DIMENSIONAL NORMAL LOCAL RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 239-268
- Print publication:
- March 2023
-
- Article
- Export citation
AUTOMORPHISMS AND SYMPLECTIC LEAVES OF CALOGERO–MOSER SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 26-57
- Print publication:
- August 2023
-
- Article
- Export citation
Hodge filtration on local cohomology, Du Bois complex and local cohomological dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 03 October 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation