No CrossRef data available.
Article contents
On the topology of the transversal slice of a quasi-homogeneous map germ
Published online by Cambridge University Press: 06 October 2023
Abstract
We consider a corank 1, finitely determined, quasi-homogeneous map germ f from 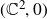 $(\mathbb{C}^2,0)$ to
$(\mathbb{C}^2,0)$ to 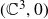 $(\mathbb{C}^3,0)$. We describe the embedded topological type of a generic hyperplane section of
$(\mathbb{C}^3,0)$. We describe the embedded topological type of a generic hyperplane section of  $f(\mathbb{C}^2)$, denoted by
$f(\mathbb{C}^2)$, denoted by 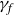 $\gamma_f$, in terms of the weights and degrees of f. As a consequence, a necessary condition for a corank 1 finitely determined map germ
$\gamma_f$, in terms of the weights and degrees of f. As a consequence, a necessary condition for a corank 1 finitely determined map germ 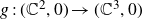 $g\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$ to be quasi-homogeneous is that the plane curve
$g\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$ to be quasi-homogeneous is that the plane curve 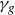 $\gamma_g$ has either two or three characteristic exponents. As an application of our main result, we also show that any one-parameter unfolding
$\gamma_g$ has either two or three characteristic exponents. As an application of our main result, we also show that any one-parameter unfolding 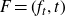 $F=(f_t,t)$ of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular.
$F=(f_t,t)$ of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular.
MSC classification
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 2 , March 2024 , pp. 339 - 359
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

