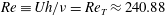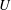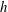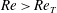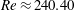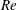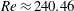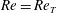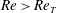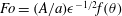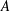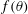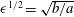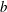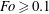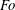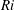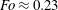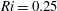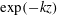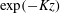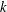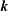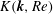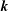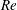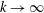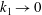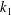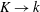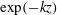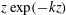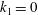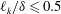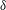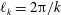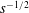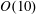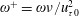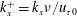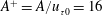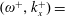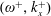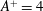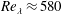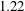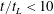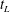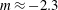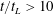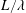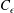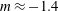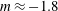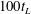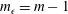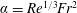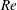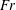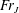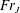JFM Rapids
Prandtl–Batchelor theorem for flows with quasiperiodic time dependence
- Hassan Arbabi, Igor Mezić
-
- Published online by Cambridge University Press:
- 07 January 2019, R1
-
- Article
- Export citation
-
The classical Prandtl–Batchelor theorem (Prandtl, Proc. Intl Mathematical Congress, Heidelberg, 1904, pp. 484–491; Batchelor, J. Fluid Mech., vol. 1 (02), 1956, pp. 177–190) states that in the regions of steady 2D flow where viscous forces are small and streamlines are closed, the vorticity is constant. In this paper, we extend this theorem to recirculating flows with quasiperiodic time dependence using ergodic and geometric analysis of Lagrangian dynamics. In particular, we show that 2D quasiperiodic viscous flows, in the limit of zero viscosity, cannot converge to recirculating inviscid flows with non-uniform vorticity distribution. A corollary of this result is that if the vorticity contours form a family of closed curves in a quasiperiodic viscous flow, then at the limit of zero viscosity, vorticity is constant in the area enclosed by those curves at all times.
The onset of transient turbulence in minimal plane Couette flow
- Julius Rhoan T. Lustro, Genta Kawahara, Lennaert van Veen, Masaki Shimizu, Hiroshi Kokubu
-
- Published online by Cambridge University Press:
- 10 January 2019, R2
-
- Article
- Export citation
-
The onset of transient turbulence in minimal plane Couette flow has been identified theoretically as homoclinic tangency with respect to a simple edge state for the Navier–Stokes equation, i.e., the gentle periodic orbit (the lower branch of a saddle-node pair) found by Kawahara & Kida (J. Fluid Mech., vol. 449, 2001, pp. 291–300). The first tangency of a pair of distinct homoclinic orbits to this periodic edge state has been discovered at Reynolds number
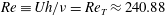 $Re\equiv Uh/\unicode[STIX]{x1D708}=Re_{T}\approx 240.88$ (
$Re\equiv Uh/\unicode[STIX]{x1D708}=Re_{T}\approx 240.88$ (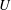 $U$,
$U$, 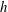 $h$, and
$h$, and  $\unicode[STIX]{x1D708}$ being half the difference of the two wall velocities, half the wall separation, and the kinematic viscosity of fluid, respectively). At
$\unicode[STIX]{x1D708}$ being half the difference of the two wall velocities, half the wall separation, and the kinematic viscosity of fluid, respectively). At 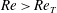 $Re>Re_{T}$ a Smale horseshoe appears on the Poincaré section through transversal homoclinic points to generate a transient chaos that eventually relaminarises. In numerical experiments a sustaining chaos, which is a consequence of period-doubling cascade stemming from the upper branch of another saddle-node pair of periodic orbits, is observed in a narrow range of the Reynolds number,
$Re>Re_{T}$ a Smale horseshoe appears on the Poincaré section through transversal homoclinic points to generate a transient chaos that eventually relaminarises. In numerical experiments a sustaining chaos, which is a consequence of period-doubling cascade stemming from the upper branch of another saddle-node pair of periodic orbits, is observed in a narrow range of the Reynolds number, 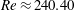 $Re\approx 240.40$–240.46. At the upper edge of this
$Re\approx 240.40$–240.46. At the upper edge of this 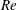 $Re$ range it is found that the chaotic set touches the lower branch of this pair, i.e., another edge state. The corresponding chaotic attractor is replaced by a chaotic saddle at
$Re$ range it is found that the chaotic set touches the lower branch of this pair, i.e., another edge state. The corresponding chaotic attractor is replaced by a chaotic saddle at 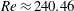 $Re\approx 240.46$, and subsequently this saddle touches the gentle periodic edge state on the boundary of the laminar basin at the tangency Reynolds number
$Re\approx 240.46$, and subsequently this saddle touches the gentle periodic edge state on the boundary of the laminar basin at the tangency Reynolds number 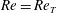 $Re=Re_{T}$. After this crisis on the boundary of the laminar basin, for
$Re=Re_{T}$. After this crisis on the boundary of the laminar basin, for 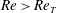 $Re>Re_{T}$, chaotic transients that eventually relaminarise can be observed.
$Re>Re_{T}$, chaotic transients that eventually relaminarise can be observed.
Water entry of spheres with various contact angles
- Nathan B. Speirs, Mohammad M. Mansoor, Jesse Belden, Tadd T. Truscott
-
- Published online by Cambridge University Press:
- 10 January 2019, R3
-
- Article
- Export citation
-
It is well known that the water entry of a sphere causes cavity formation above a critical impact velocity as a function of the solid–liquid contact angle; Duez et al. (Nat. Phys., vol. 3 (3), 2007, pp. 180–183). Using a rough sphere with a contact angle of
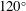 $120^{\circ }$, Aristoff & Bush (J. Fluid Mech., vol. 619, 2009, pp. 45–78) showed that there are four different cavity shapes dependent on the Bond and Weber numbers (i.e., quasistatic, shallow, deep and surface). We experimentally alter the Bond number, Weber number and contact angle of smooth spheres and find two key additions to the literature: (1) cavity shape also depends on the contact angle; (2) the absence of a splash crown at low Weber number results in cavity formation below the predicted critical velocity. In addition, we use alternate scales in defining the Bond, Weber and Froude numbers to predict the cavity shapes and scale pinch-off times for various impacting bodies (e.g., spheres, multidroplet streams and jets) on the same plots, merging the often separated studies of solid–liquid and liquid–liquid impact in the literature.
$120^{\circ }$, Aristoff & Bush (J. Fluid Mech., vol. 619, 2009, pp. 45–78) showed that there are four different cavity shapes dependent on the Bond and Weber numbers (i.e., quasistatic, shallow, deep and surface). We experimentally alter the Bond number, Weber number and contact angle of smooth spheres and find two key additions to the literature: (1) cavity shape also depends on the contact angle; (2) the absence of a splash crown at low Weber number results in cavity formation below the predicted critical velocity. In addition, we use alternate scales in defining the Bond, Weber and Froude numbers to predict the cavity shapes and scale pinch-off times for various impacting bodies (e.g., spheres, multidroplet streams and jets) on the same plots, merging the often separated studies of solid–liquid and liquid–liquid impact in the literature.
Nonlinear aspects of focusing internal waves
- Natalia D. Shmakova, Jan-Bert Flór
-
- Published online by Cambridge University Press:
- 11 January 2019, R4
-
- Article
- Export citation
-
When a torus oscillates horizontally in a linearly stratified fluid, the wave rays form a double cone, one upward and one downward, with two focal points where the wave amplitude has a maximum due to wave focusing. Following a former study on linear aspects of wave focusing (Ermanyuk et al., J. Fluid Mech., vol. 813, 2017, pp. 695–715), we here consider experimental results on the nonlinear aspects that occur in the focal region below the torus for higher-amplitude forcing. A new non-dimensional number that is based on heuristic arguments for the wave amplitude in the focal area is presented. This focusing number is defined as
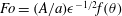 $Fo=(A/a)\unicode[STIX]{x1D716}^{-1/2}f(\unicode[STIX]{x1D703})$, with oscillation amplitude
$Fo=(A/a)\unicode[STIX]{x1D716}^{-1/2}f(\unicode[STIX]{x1D703})$, with oscillation amplitude 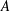 $A$,
$A$, 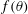 $f(\unicode[STIX]{x1D703})$ a function for the variation of the wave amplitude with wave angle
$f(\unicode[STIX]{x1D703})$ a function for the variation of the wave amplitude with wave angle 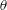 $\unicode[STIX]{x1D703}$, and
$\unicode[STIX]{x1D703}$, and 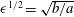 $\unicode[STIX]{x1D716}^{1/2}=\sqrt{b/a}$ the increase in amplitude due to the focusing, with
$\unicode[STIX]{x1D716}^{1/2}=\sqrt{b/a}$ the increase in amplitude due to the focusing, with  $a$ and
$a$ and 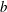 $b$, respectively, the minor and major radius of the torus. Nonlinear effects occur for
$b$, respectively, the minor and major radius of the torus. Nonlinear effects occur for 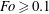 $Fo\geqslant 0.1$, with the shear stress giving rise to a mean flow which results in the focal region in a central upward motion partially surrounded by a downward motion. With increasing
$Fo\geqslant 0.1$, with the shear stress giving rise to a mean flow which results in the focal region in a central upward motion partially surrounded by a downward motion. With increasing 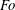 $Fo$, the Richardson number
$Fo$, the Richardson number 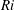 $Ri$ measured from the wave steepness monotonically decreases. Wave breaking occurs at
$Ri$ measured from the wave steepness monotonically decreases. Wave breaking occurs at 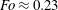 $Fo\approx 0.23$, corresponding to
$Fo\approx 0.23$, corresponding to 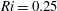 $Ri=0.25$. In this regime, the focal region is unstable due to triadic wave resonance. For the different tori sizes under consideration, the triadic resonant instability in these three-dimensional flows resembles closely the resonance observed by Bourget et al. (J. Fluid Mech., vol. 723, 2013, pp. 1–20) for a two-dimensional flow, with only minor differences. Application to internal tidal waves in the ocean are discussed.
$Ri=0.25$. In this regime, the focal region is unstable due to triadic wave resonance. For the different tori sizes under consideration, the triadic resonant instability in these three-dimensional flows resembles closely the resonance observed by Bourget et al. (J. Fluid Mech., vol. 723, 2013, pp. 1–20) for a two-dimensional flow, with only minor differences. Application to internal tidal waves in the ocean are discussed.
On the decay of dispersive motions in the outer region of rough-wall boundary layers
- Johan Meyers, Bharathram Ganapathisubramani, Raúl Bayoán Cal
-
- Published online by Cambridge University Press:
- 25 January 2019, R5
-
- Article
- Export citation
-
In rough-wall boundary layers, wall-parallel non-homogeneous mean-flow solutions exist that lead to so-called dispersive velocity components and dispersive stresses. They play a significant role in the mean-flow momentum balance near the wall, but typically disappear in the outer layer. A theoretical framework is presented to study the decay of dispersive motions in the outer layer. To this end, the problem is formulated in Fourier space, and a set of governing ordinary differential equations per mode in wavenumber space is derived by linearizing the Reynolds-averaged Navier–Stokes equations around a constant background velocity. With further simplifications, analytically tractable solutions are found consisting of linear combinations of
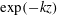 $\exp (-kz)$ and
$\exp (-kz)$ and 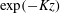 $\exp (-Kz)$, with
$\exp (-Kz)$, with  $z$ the wall distance,
$z$ the wall distance, 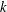 $k$ the magnitude of the horizontal wavevector
$k$ the magnitude of the horizontal wavevector 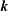 $\boldsymbol{k}$, and where
$\boldsymbol{k}$, and where 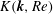 $K(\boldsymbol{k},Re)$ is a function of
$K(\boldsymbol{k},Re)$ is a function of 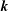 $\boldsymbol{k}$ and the Reynolds number
$\boldsymbol{k}$ and the Reynolds number 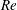 $Re$. Moreover, for
$Re$. Moreover, for 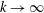 $k\rightarrow \infty$ or
$k\rightarrow \infty$ or 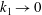 $k_{1}\rightarrow 0$ (with
$k_{1}\rightarrow 0$ (with 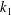 $k_{1}$ the stream-wise wavenumber),
$k_{1}$ the stream-wise wavenumber), 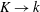 $K\rightarrow k$ is found, in which case solutions consist of a linear combination of
$K\rightarrow k$ is found, in which case solutions consist of a linear combination of 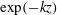 $\exp (-kz)$ and
$\exp (-kz)$ and 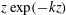 $z\exp (-kz)$, and are independent of the Reynolds number. These analytical relations are compared in the limit of
$z\exp (-kz)$, and are independent of the Reynolds number. These analytical relations are compared in the limit of 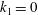 $k_{1}=0$ to the rough boundary layer experiments by Vanderwel & Ganapathisubramani (J. Fluid Mech., vol. 774, 2015, R2) and are in reasonable agreement for
$k_{1}=0$ to the rough boundary layer experiments by Vanderwel & Ganapathisubramani (J. Fluid Mech., vol. 774, 2015, R2) and are in reasonable agreement for 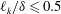 $\ell _{k}/\unicode[STIX]{x1D6FF}\leqslant 0.5$, with
$\ell _{k}/\unicode[STIX]{x1D6FF}\leqslant 0.5$, with 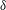 $\unicode[STIX]{x1D6FF}$ the boundary-layer thickness and
$\unicode[STIX]{x1D6FF}$ the boundary-layer thickness and 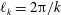 $\ell _{k}=2\unicode[STIX]{x03C0}/k$.
$\ell _{k}=2\unicode[STIX]{x03C0}/k$.
Focus on Fluids
Dropping slender-body theory into the mud
- S. E. Spagnolie
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 1-4
-
- Article
-
- You have access Access
- HTML
- Export citation
-
The equations describing classical viscous fluid flow are notoriously challenging to solve, even approximately, when the flow is host to one or many immersed bodies. When an immersed body is slender, the smallness of its aspect ratio can sometimes be used as a basis for a ‘slender-body theory’ describing its interaction with the surrounding environment. If the fluid is complex, however, such theories are generally invalid and efforts to understand the dynamics of immersed bodies are almost entirely numerical in nature. In a valiant effort, Hewitt & Balmforth (J. Fluid Mech., vol. 856, 2018, pp. 870–897) have unearthed a theory to describe the motion of slender bodies in a viscoplastic fluid, ‘fluids’ such as mud or toothpaste which can be coaxed to flow, but only with a sufficiently large amount of forcing. Mathematical theories for some tremendously complicated physical systems may now be within reach.
JFM Papers
A rarefied gas flow around a rotating sphere: diverging profiles of gradients of macroscopic quantities
- Satoshi Taguchi, Kazuyuki Saito, Shigeru Takata
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 5-33
-
- Article
-
- You have access Access
- Open access
- HTML
- Export citation
-
The steady behaviour of a rarefied gas around a rotating sphere is studied numerically on the basis of the linearised ellipsoidal statistical model of the Boltzmann equation, also known as the ES model, and the Maxwell diffuse–specular boundary condition. It is demonstrated numerically that the normal derivative of the circumferential component of the flow velocity and that of the heat flux diverge on the boundary with a rate
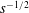 $s^{-1/2}$, where
$s^{-1/2}$, where  $s$ is the normal distance from the boundary. Further, it is demonstrated that the diverging term is proportional to the magnitude of the jump discontinuity of the velocity distribution function on the boundary, which originates from the mismatch of the incoming and outgoing data on the boundary. The moment of force exerted on the sphere is also obtained for a wide range of the Knudsen number and for various values of the accommodation coefficient.
$s$ is the normal distance from the boundary. Further, it is demonstrated that the diverging term is proportional to the magnitude of the jump discontinuity of the velocity distribution function on the boundary, which originates from the mismatch of the incoming and outgoing data on the boundary. The moment of force exerted on the sphere is also obtained for a wide range of the Knudsen number and for various values of the accommodation coefficient.
Hydrodynamics of periodic wave energy converter arrays
- Grgur Tokić, Dick K. P. Yue
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 34-74
-
- Article
- Export citation
-
We consider the hydrodynamics of wave energy converter (WEC) arrays consisting of periodically repeated single bodies or sub-arrays. Of special interest is the array gain due to wave interactions as a function of the spatial configuration of the array. For simplicity, we assume identical WECs oscillating in heave only, although the results should extend to general motions. We find that array gains can be as high as
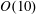 $O(10)$ compared to the same WECs operating in isolation. We show that prominent decreases in array gain are associated with Laue resonances, involving the incident and scattered wave modes, for which we obtain an explicit condition. We also show theoretically that Bragg resonances can result in large decreases in gain with as few as two rows of strong absorbers. For general WEC geometries, we develop a multiple-scattering method of wave–body interactions applicable to generally spaced periodic arrays. For arrays of truncated vertical cylinders, we perform numerical investigations confirming our theoretical predictions for Laue and Bragg resonances. For a special class of multiple-row rectangular WEC arrays, our numerical results show that motion-trapped Rayleigh–Bloch waves can exist and be excited by an incident wave, resulting in sharp, narrow-banded spikes in the array gain.
$O(10)$ compared to the same WECs operating in isolation. We show that prominent decreases in array gain are associated with Laue resonances, involving the incident and scattered wave modes, for which we obtain an explicit condition. We also show theoretically that Bragg resonances can result in large decreases in gain with as few as two rows of strong absorbers. For general WEC geometries, we develop a multiple-scattering method of wave–body interactions applicable to generally spaced periodic arrays. For arrays of truncated vertical cylinders, we perform numerical investigations confirming our theoretical predictions for Laue and Bragg resonances. For a special class of multiple-row rectangular WEC arrays, our numerical results show that motion-trapped Rayleigh–Bloch waves can exist and be excited by an incident wave, resulting in sharp, narrow-banded spikes in the array gain.
Drag reduction in turbulent flows along a cylinder by streamwise-travelling waves of circumferential wall velocity
- Ming-Xiang Zhao, Wei-Xi Huang, Chun-Xiao Xu
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 75-98
-
- Article
- Export citation
-
Drag reduction at the external surface of a cylinder in turbulent flows along the axial direction by circumferential wall motion is studied by direct numerical simulations. The circumferential wall oscillation can lead to drag reduction due to the formation of a Stokes layer, but it may also result in centrifugal instability, which can enhance turbulence and increase drag. In the present work, the Reynolds number based on the reference friction velocity and the nominal thickness of the boundary layer is 272. A map describing the relationship between the drag-reduction rate and the control parameters, namely, the angular frequency
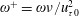 $\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}^{2}$ and the streamwise wavenumber
$\unicode[STIX]{x1D714}^{+}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}^{2}$ and the streamwise wavenumber 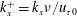 $k_{x}^{+}=k_{x}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}$, is obtained at the oscillation amplitude of
$k_{x}^{+}=k_{x}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}0}$, is obtained at the oscillation amplitude of 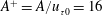 ${A^{+}=A/u}_{\unicode[STIX]{x1D70F}0}=16$, where
${A^{+}=A/u}_{\unicode[STIX]{x1D70F}0}=16$, where 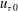 $u_{\unicode[STIX]{x1D70F}0}$ is the friction velocity of the uncontrolled flow and
$u_{\unicode[STIX]{x1D70F}0}$ is the friction velocity of the uncontrolled flow and  $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. The maximum drag-reduction rate and the maximum drag-increase rate are both approximately 48 %, which are respectively attained at
$\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. The maximum drag-reduction rate and the maximum drag-increase rate are both approximately 48 %, which are respectively attained at 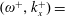 $(\unicode[STIX]{x1D714}^{+},k_{x}^{+})=$ (0.0126, 0.0148) and (0.0246, 0.0018). The drag-reduction rate can be scaled well with the help of the effective thickness of the Stokes layer. The drag increase is observed in a narrow triangular region in the frequency–wavenumber plane. The vortices induced by the centrifugal instability become the primary coherent structure in the near-wall region, and they are closely correlated with the high skin friction. In these drag-increase cases, the effective control frequency or wavenumber is crucial in scaling the drag-increase rate. As the wall curvature normalised by the boundary layer thickness becomes larger, the drag-increase region in the
$(\unicode[STIX]{x1D714}^{+},k_{x}^{+})=$ (0.0126, 0.0148) and (0.0246, 0.0018). The drag-reduction rate can be scaled well with the help of the effective thickness of the Stokes layer. The drag increase is observed in a narrow triangular region in the frequency–wavenumber plane. The vortices induced by the centrifugal instability become the primary coherent structure in the near-wall region, and they are closely correlated with the high skin friction. In these drag-increase cases, the effective control frequency or wavenumber is crucial in scaling the drag-increase rate. As the wall curvature normalised by the boundary layer thickness becomes larger, the drag-increase region in the 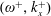 $(\unicode[STIX]{x1D714}^{+},k_{x}^{+})$ plane as well as the maximum drag-increase rate also become larger. Net energy saving with a considerable drag-reduction rate is possible when reducing the oscillation amplitude. At
$(\unicode[STIX]{x1D714}^{+},k_{x}^{+})$ plane as well as the maximum drag-increase rate also become larger. Net energy saving with a considerable drag-reduction rate is possible when reducing the oscillation amplitude. At 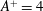 $A^{+}=4$, a net energy saving of 18 % can be achieved with a drag-reduction rate of 25 % if only the power dissipation due to viscous stress is taken into account in an ideal actuation system.
$A^{+}=4$, a net energy saving of 18 % can be achieved with a drag-reduction rate of 25 % if only the power dissipation due to viscous stress is taken into account in an ideal actuation system.
Laboratory experiments on the temporal decay of homogeneous anisotropic turbulence
- L. B. Esteban, J. S. Shrimpton, B. Ganapathisubramani
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 99-127
-
- Article
- Export citation
-
We experimentally investigate the temporal decay of homogeneous anisotropic turbulence, monitoring the evolution of velocity fluctuations, dissipation and turbulent length scales over time. We employ an apparatus in which two facing random jet arrays of water pumps generate turbulence with negligible mean flow and shear over a volume that is much larger than the initial characteristic turbulent large scale of the flow. The Reynolds number based on the Taylor microscale for forced turbulence is
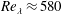 $Re_{\unicode[STIX]{x1D706}}\approx 580$ and the axial-to-radial ratio of the root mean square velocity fluctuations is
$Re_{\unicode[STIX]{x1D706}}\approx 580$ and the axial-to-radial ratio of the root mean square velocity fluctuations is 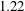 $1.22$. Two velocity components are measured by particle image velocimetry at the symmetry plane of the water tank. Measurements are taken for both ‘stationary’ forced turbulence and natural decaying turbulence. For decaying turbulence, power-law fits to the decay of turbulent kinetic energy reveal two regions over time; in the near-field region (
$1.22$. Two velocity components are measured by particle image velocimetry at the symmetry plane of the water tank. Measurements are taken for both ‘stationary’ forced turbulence and natural decaying turbulence. For decaying turbulence, power-law fits to the decay of turbulent kinetic energy reveal two regions over time; in the near-field region (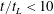 $t/t_{L}<10$,
$t/t_{L}<10$, 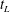 $t_{L}$ is the integral time scale of the forced turbulence) a decay exponent
$t_{L}$ is the integral time scale of the forced turbulence) a decay exponent 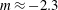 $m\approx -2.3$ is found whereas for the far-field region (
$m\approx -2.3$ is found whereas for the far-field region (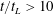 $t/t_{L}>10$) the value of the decay exponent was found to be affected by turbulence saturation. The near-field exhibits features of non-equilibrium turbulence with constant
$t/t_{L}>10$) the value of the decay exponent was found to be affected by turbulence saturation. The near-field exhibits features of non-equilibrium turbulence with constant 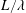 $L/\unicode[STIX]{x1D706}$ and varying
$L/\unicode[STIX]{x1D706}$ and varying 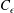 $C_{\unicode[STIX]{x1D716}}$ (dissipation constant). We found a decay exponent
$C_{\unicode[STIX]{x1D716}}$ (dissipation constant). We found a decay exponent 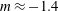 $m\approx -1.4$ for the unsaturated regime and
$m\approx -1.4$ for the unsaturated regime and 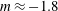 $m\approx -1.8$ for the saturated regime, in good agreement with previous numerical and experimental studies. We also observe a fast evolution towards isotropy at small scales, whereas anisotropy at large scales remains in the flow over more than
$m\approx -1.8$ for the saturated regime, in good agreement with previous numerical and experimental studies. We also observe a fast evolution towards isotropy at small scales, whereas anisotropy at large scales remains in the flow over more than 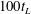 $100t_{L}$. Direct estimates of dissipation are obtained and the decay exponent agrees well with the prediction
$100t_{L}$. Direct estimates of dissipation are obtained and the decay exponent agrees well with the prediction 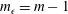 $m_{\unicode[STIX]{x1D716}}=m-1$ throughout the decay process.
$m_{\unicode[STIX]{x1D716}}=m-1$ throughout the decay process.
The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids
- Yunpeng Wang, Roger E. Khayat
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 128-161
-
- Article
- Export citation
-
The free-surface flow formed by a circular jet impinging on a stationary disk is analysed theoretically. We develop a simple and coherent model to predict the location and height of the jump for high-viscosity liquids. The study explores the effect of gravity in the supercritical flow. The formulation reduces to a problem, involving only one parameter:
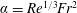 $\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$, where
$\unicode[STIX]{x1D6FC}=Re^{1/3}Fr^{2}$, where 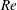 $Re$ and
$Re$ and 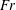 $Fr$ are the Reynolds and Froude numbers based on the flow rate and the jet radius. We show that the jump location coincides with the singularity in the thin-film equation when gravity is included, suggesting that the jump location can be determined without the knowledge of downstream flow conditions such as the jump height, the radius of the disk, which corroborates earlier observations in the case of type I circular hydraulic jumps. Consequently, there is no need for a boundary condition downstream to determine the jump radius. Our results corroborate well existing measurements and numerical simulation. Our predictions also confirm the constancy of the Froude number
$Fr$ are the Reynolds and Froude numbers based on the flow rate and the jet radius. We show that the jump location coincides with the singularity in the thin-film equation when gravity is included, suggesting that the jump location can be determined without the knowledge of downstream flow conditions such as the jump height, the radius of the disk, which corroborates earlier observations in the case of type I circular hydraulic jumps. Consequently, there is no need for a boundary condition downstream to determine the jump radius. Our results corroborate well existing measurements and numerical simulation. Our predictions also confirm the constancy of the Froude number 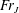 $Fr_{J}$ based on the jump radius and height as suggested by the measurements of Duchesne et al. (Europhys. Lett., vol. 107, 2014, 54002). We establish theoretically the conditions for
$Fr_{J}$ based on the jump radius and height as suggested by the measurements of Duchesne et al. (Europhys. Lett., vol. 107, 2014, 54002). We establish theoretically the conditions for 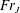 $Fr_{J}$ to remain independent of the flow rate. The subcritical flow and the height of the hydraulic jump are sought subject to the thickness at the edge of the disk, comprising contributions based on the capillary length and minimum flow energy. The thickness at the edge of the disk appears to be negligibly small for high-viscosity liquids.
$Fr_{J}$ to remain independent of the flow rate. The subcritical flow and the height of the hydraulic jump are sought subject to the thickness at the edge of the disk, comprising contributions based on the capillary length and minimum flow energy. The thickness at the edge of the disk appears to be negligibly small for high-viscosity liquids.
A simple system for moist convection: the Rainy–Bénard model
- Geoffrey K. Vallis, Douglas J. Parker, Steven M. Tobias
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 162-199
-
- Article
- Export citation
-
Rayleigh–Bénard convection is one of the most well-studied models in fluid mechanics. Atmospheric convection, one of the most important components of the climate system, is by comparison complicated and poorly understood. A key attribute of atmospheric convection is the buoyancy source provided by the condensation of water vapour, but the presence of radiation, compressibility, liquid water and ice further complicate the system and our understanding of it. In this paper we present an idealized model of moist convection by taking the Boussinesq limit of the ideal-gas equations and adding a condensate that obeys a simplified Clausius–Clapeyron relation. The system allows moist convection to be explored at a fundamental level and reduces to the classical Rayleigh–Bénard model if the latent heat of condensation is taken to be zero. The model has an exact, Rayleigh-number-independent ‘drizzle’ solution in which the diffusion of water vapour from a saturated lower surface is balanced by condensation, with the temperature field (and so the saturation value of the moisture) determined self-consistently by the heat released in the condensation. This state is the moist analogue of the conductive solution in the classical problem. We numerically determine the linear stability properties of this solution as a function of Rayleigh number and a non-dimensional latent-heat parameter. We also present some two-dimensional, time-dependent, nonlinear solutions at various values of Rayleigh number and the non-dimensional condensational parameters. At sufficiently low Rayleigh number the system converges to the drizzle solution, and we find no evidence that two-dimensional self-sustained convection can occur when that solution is stable. The flow transitions from steady to turbulent as the Rayleigh number or the effects of condensation are increased, with plumes triggered by gravity waves emanating from other plumes. The interior dries as the level of turbulence increases, because the plumes entrain more dry air and because the saturated boundary layer at the top becomes thinner. The flow develops a broad relative humidity minimum in the domain interior, only weakly dependent on Rayleigh number when that is high.
System identification of a low-density jet via its noise-induced dynamics
- Minwoo Lee, Yuanhang Zhu, Larry K. B. Li, Vikrant Gupta
-
- Published online by Cambridge University Press:
- 08 January 2019, pp. 200-215
-
- Article
- Export citation
-
Low-density jets are central to many natural and industrial processes. Under certain conditions, they can develop global oscillations at a limit cycle, behaving as a prototypical example of a self-excited hydrodynamic oscillator. In this study, we perform system identification of a low-density jet using measurements of its noise-induced dynamics in the unconditionally stable regime, prior to both the Hopf and saddle-node points. We show that this approach can enable prediction of (i) the order of nonlinearity, (ii) the locations and types of the bifurcation points (and hence the stability boundaries) and (iii) the resulting limit-cycle oscillations. The only assumption made about the system is that it obeys a Stuart–Landau equation in the vicinity of the Hopf point, thus making the method applicable to a variety of hydrodynamic systems. This study constitutes the first experimental demonstration of system identification using the noise-induced dynamics in only the unconditionally stable regime, i.e. away from the regimes where limit-cycle oscillations may occur. This opens up new possibilities for the prediction and analysis of the stability and nonlinear behaviour of hydrodynamic systems.
Separated rows structure of vortex streets behind triangular objects
- Ildoo Kim
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 216-226
-
- Article
- Export citation
-
We discuss two distinct spatial structures of vortex streets. The ‘conventional mushroom’ structure is commonly discussed in many experimental studies, and the exotic ‘separated rows’ structure is characterized by a thin layer of irrotational fluid between two rows of vortices. In a two-dimensional soap film channel, we generate the exotic vortex arrangement by using triangular objects. This setting allows us to vary the thickness of boundary layers and their separation distance independently. We find that the separated rows structure appears only when the boundary layer is thinner than 40 % of the separation distance. We also discuss two physical mechanisms of the breakdown of vortex structures. The conventional mushroom structure decays due to the mixing, and the separated rows structure decays because its arrangement is hydrodynamically unstable.
Large eddy simulation of transient upstream/downstream vortex interactions
- Kyle J. Forster, Sammy Diasinos, Graham Doig, Tracie J. Barber
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 227-260
-
- Article
- Export citation
-
Experimentally validated large eddy simulations were performed on two NACA0012 vanes at various lateral offsets to observe the transient effects of the near field interactions between two streamwise vortices. The vanes were separated in the streamwise direction, allowing the upstream vortex to impact on the downstream geometry. These vanes were evaluated at an angle of incidence of
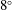 $8^{\circ }$ and a Reynolds number of 70 000, with rear vane angle reversed to create a co-rotating or counter-rotating vortex pair. The downstream vortex merged with the upstream in the co-rotating condition, driven by the suppression of one of the tip vortices of the downstream vane. At close proximity to the pressure side, the vane elongated the upstream vortex, resulting in it being the weakened and merging into the downstream vortex. This produced a transient production of bifurcated vortices in the wake region. The downstream vortex of the co-rotating pair experienced faster meandering growth, with position oscillations equalising between the vortices. The position oscillation was determined to be responsible for statistical variance in the merging location, with variation in vortex separation causing the vortices at a single plane to merge and separate in a time-dependent manner. In the counter-rotating condition position oscillations were found to be larger, with higher growth, but less uniform periodicity. It was found that the circulation transfer between the vortices was linked to the magnitude of their separation, with high separation fluctuations weakening the upstream vortex and strengthening the downstream vortex. In the case of upstream vortex impingement on the downstream vane, the upstream vortex was found to bifurcate, with a four vortex system being formed by interactions with the shear layer. This eventually resulted in a single dominant vortex, which did not magnify its oscillation amplitudes as it travelled downstream due to the destruction of the interacting vortices.
$8^{\circ }$ and a Reynolds number of 70 000, with rear vane angle reversed to create a co-rotating or counter-rotating vortex pair. The downstream vortex merged with the upstream in the co-rotating condition, driven by the suppression of one of the tip vortices of the downstream vane. At close proximity to the pressure side, the vane elongated the upstream vortex, resulting in it being the weakened and merging into the downstream vortex. This produced a transient production of bifurcated vortices in the wake region. The downstream vortex of the co-rotating pair experienced faster meandering growth, with position oscillations equalising between the vortices. The position oscillation was determined to be responsible for statistical variance in the merging location, with variation in vortex separation causing the vortices at a single plane to merge and separate in a time-dependent manner. In the counter-rotating condition position oscillations were found to be larger, with higher growth, but less uniform periodicity. It was found that the circulation transfer between the vortices was linked to the magnitude of their separation, with high separation fluctuations weakening the upstream vortex and strengthening the downstream vortex. In the case of upstream vortex impingement on the downstream vane, the upstream vortex was found to bifurcate, with a four vortex system being formed by interactions with the shear layer. This eventually resulted in a single dominant vortex, which did not magnify its oscillation amplitudes as it travelled downstream due to the destruction of the interacting vortices.
Droplet levitation over a moving wall with a steady air film
- Erina Sawaguchi, Ayumi Matsuda, Kai Hama, Masafumi Saito, Yoshiyuki Tagawa
-
- Published online by Cambridge University Press:
- 08 January 2019, pp. 261-282
-
- Article
-
- You have access Access
- Open access
- HTML
- Export citation
-
In isothermal non-coalescence behaviours of a droplet against a wall, an air film of micrometre thickness plays a crucial role. We experimentally study this phenomenon by letting a droplet levitate over a moving glass wall. The three-dimensional shape of the air film is measured using an interferometric method. The mean curvature distribution of the deformed free surface and the distributions of the lubrication pressure are derived from the experimental measurements. We vary experimental parameters, namely wall velocity, droplet diameter and viscosity of the droplets, over a wide range; for example, the droplet viscosity is varied over two orders of magnitude. For the same wall velocity, the air film of low-viscosity droplets shows little shape oscillation with constant film thickness (defined as the steady state), while that of highly viscous droplets shows a significant shape oscillation with varying film thickness (defined as the unsteady state). The droplet viscosity also affects the surface velocity of a droplet. Under our experimental conditions, where the air film shape can be assumed to be steady, we present experimental evidence showing that the lift force generated inside the air film balances with the droplet’s weight. We also verify that the lubrication pressure locally balances with the surface tension and hydrostatic pressures. This indicates that lubrication pressure and the shape of the free surface are mutually determined. Based on the local pressure balance, we discuss a process of determining the steady shape of an air film that has two areas of minimum thickness in the vicinity of the downstream rim.
Macroscopic model for unsteady flow in porous media
- Didier Lasseux, Francisco J. Valdés-Parada, Fabien Bellet
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 283-311
-
- Article
- Export citation
-
The present article reports on a formal derivation of a macroscopic model for unsteady one-phase incompressible flow in rigid and periodic porous media using an upscaling technique. The derivation is carried out in the time domain in the general situation where inertia may have a significant impact. The resulting model is non-local in time and involves two effective coefficients in the macroscopic filtration law, namely a dynamic apparent permeability tensor,
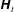 $\unicode[STIX]{x1D643}_{t}$, and a vector,
$\unicode[STIX]{x1D643}_{t}$, and a vector,  $\unicode[STIX]{x1D736}$, accounting for the time-decaying influence of the flow initial condition. This model generalizes previous non-local macroscale models restricted to creeping flow conditions. Ancillary closure problems are provided, which allow the effective coefficients to be computed. Symmetry and positiveness analyses of
$\unicode[STIX]{x1D736}$, accounting for the time-decaying influence of the flow initial condition. This model generalizes previous non-local macroscale models restricted to creeping flow conditions. Ancillary closure problems are provided, which allow the effective coefficients to be computed. Symmetry and positiveness analyses of 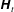 $\unicode[STIX]{x1D643}_{t}$ are carried out, showing that this tensor is symmetric only in the creeping regime. The effective coefficients are functions of time, geometry, macroscopic forcings and the initial flow condition. This is illustrated through numerical solutions of the closure problems. Predictions are made on a simple periodic structure for a wide range of Reynolds numbers smaller than the critical value characterizing the first Hopf bifurcation. Finally, the performance of the macroscopic model for a variety of macroscopic forcings and initial conditions is examined in several case studies. Validation through comparisons with direct numerical simulations is performed. It is shown that the purely heuristic classical model, widely used for unsteady flow, consisting of a Darcy-like model complemented with an accumulation term on the filtration velocity, is inappropriate.
$\unicode[STIX]{x1D643}_{t}$ are carried out, showing that this tensor is symmetric only in the creeping regime. The effective coefficients are functions of time, geometry, macroscopic forcings and the initial flow condition. This is illustrated through numerical solutions of the closure problems. Predictions are made on a simple periodic structure for a wide range of Reynolds numbers smaller than the critical value characterizing the first Hopf bifurcation. Finally, the performance of the macroscopic model for a variety of macroscopic forcings and initial conditions is examined in several case studies. Validation through comparisons with direct numerical simulations is performed. It is shown that the purely heuristic classical model, widely used for unsteady flow, consisting of a Darcy-like model complemented with an accumulation term on the filtration velocity, is inappropriate.
Thermophoresis of a spherical particle: modelling through moment-based, macroscopic transport equations
- Juan C. Padrino, James E. Sprittles, Duncan A. Lockerby
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 312-347
-
- Article
-
- You have access Access
- Open access
- HTML
- Export citation
-
We consider the linearized form of the regularized 13-moment equations (R13) to model the slow, steady gas dynamics surrounding a rigid, heat-conducting sphere when a uniform temperature gradient is imposed far from the sphere and the gas is in a state of rarefaction. Under these conditions, the phenomenon of thermophoresis, characterized by forces on the solid surfaces, occurs. The R13 equations, derived from the Boltzmann equation using the moment method, provide closure to the mass, momentum and energy conservation laws in the form of constitutive, transport equations for the stress and heat flux that extend the Navier–Stokes–Fourier model to include non-equilibrium effects. We obtain analytical solutions for the field variables that characterize the gas dynamics and a closed-form expression for the thermophoretic force on the sphere. We also consider the slow, streaming flow of gas past a sphere using the same model resulting in a drag force on the body. The thermophoretic velocity of the sphere is then determined from the balance between thermophoretic force and drag. The thermophoretic force is compared with predictions from other theories, including Grad’s 13-moment equations (G13), variants of the Boltzmann equation commonly used in kinetic theory, and with recently published experimental data. The new results from R13 agree well with results from kinetic theory up to a Knudsen number (based on the sphere’s radius) of approximately 0.1 for the values of solid-to-gas heat conductivity ratios considered. However, in this range of Knudsen numbers, where for a very high thermal conductivity of the solid the experiments show reversed thermophoretic forces, the R13 solution, which does result in a reversal of the force, as well as the other theories predict significantly smaller forces than the experimental values. For Knudsen numbers between 0.1 and 1 approximately, the R13 model of thermophoretic force qualitatively shows the trend exhibited by the measurements and, among the various models considered, results in the least discrepancy.
Dynamics of heavy and buoyant underwater pendulums
- Varghese Mathai, Laura A. W. M. Loeffen, Timothy T. K. Chan, Sander Wildeman
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 348-363
-
- Article
-
- You have access Access
- Open access
- HTML
- Export citation
-
The humble pendulum is often invoked as the archetype of a simple, gravity driven, oscillator. Under ideal circumstances, the oscillation frequency of the pendulum is independent of its mass and swing amplitude. However, in most real-world situations, the dynamics of pendulums is not quite so simple, particularly with additional interactions between the pendulum and a surrounding fluid. Here we extend the realm of pendulum studies to include large amplitude oscillations of heavy and buoyant pendulums in a fluid. We performed experiments with massive and hollow cylindrical pendulums in water, and constructed a simple model that takes the buoyancy, added mass, fluid (nonlinear) drag and bearing friction into account. To first order, the model predicts the oscillation frequencies, peak decelerations and damping rate well. An interesting effect of the nonlinear drag captured well by the model is that, for heavy pendulums, the damping time shows a non-monotonic dependence on pendulum mass, reaching a minimum when the pendulum mass density is nearly twice that of the fluid. Small deviations from the model’s predictions are seen, particularly in the second and subsequent maxima of oscillations. Using time-resolved particle image velocimetry (TR-PIV), we reveal that these deviations likely arise due to the disturbed flow created by the pendulum at earlier times. The mean wake velocity obtained from PIV is used to model an extra drag term due to incoming wake flow. The revised model significantly improves the predictions for the second and subsequent oscillations.
On the breakup of spiralling liquid jets
- Yuan Li, Grigori M. Sisoev, Yulii D. Shikhmurzaev
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 364-384
-
- Article
- Export citation
-
The generation of drops from a jet spiralling out of a spinning device, under the action of centrifugal force, is considered for the case of small perturbations introduced at the inlet. Close to the inlet, where the disturbances can be regarded as small, their propagation is found to be qualitatively similar to that of a wave propagating down a straight jet stretched by an external body force (e.g. gravity). The dispersion equation has the same parametric dependence on the base flow, but the base flow is, of course, different. Further down the jet, where the amplitude of the disturbances becomes finite and eventually resulting in drop formation, the flow appears to be quite complex. As shown, for the regular/periodic process of drop generation, the wavelength corresponding to the frequency at the inlet, increasing as the wave propagates down the stretching jet, determines, in general, not the volume of the resulting drop but the sum of volumes of the main drop and the satellite droplet that follows the main one. The proportion of the total volume forming the main drop depends on how far down the jet the drops are produced, i.e. on the magnitude of the inlet disturbance. The volume of the main drop is found to be a linear function of the radius of the unperturbed jet evaluated at the point where the drop breaks away from the jet. This radius, and the corresponding velocity of the base flow, have to be found simultaneously with the jet’s trajectory by using a jet-specific non-orthogonal coordinate system described in detail in Shikhmurzaev & Sisoev (J. Fluid Mech., vol. 819, 2017, pp. 352–400). Some characteristic features of the nonlinear dynamics of the drop formation are discussed.