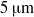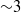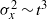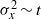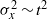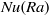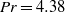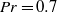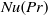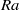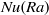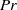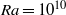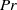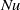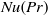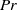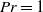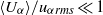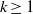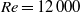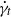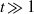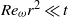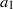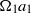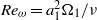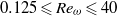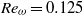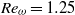Fronts, or regions with strong horizontal density gradients, are ubiquitous and dynamically important features in the ocean and atmosphere. In the atmosphere, fronts are associated with some of the most severe weather events, while in the ocean, fronts are associated with enhanced turbulence, water mass transformation and biological activity. Here, we examine the dynamics involved in the formation of fronts, or frontogenesis, in detail using a generalized mathematical framework. This extends previous work which has generally revolved around two limiting cases: fronts generated through forcing due to a convergent large-scale flow, and fronts generated spontaneously during the geostrophic adjustment of an initially unbalanced flow. Here, we introduce a new generalized momentum coordinate to simultaneously describe forced and spontaneous frontogenesis. The nonlinear, inviscid, Boussinesq, hydrostatic governing equations for uniform PV flow are solved for arbitrary Rossby and Froude number. The solution is then examined in three distinct cases. Firstly, for a zero potential vorticity (PV) flow bounded by rigid lids, a general solution is derived for the transient response of the fluid to an arbitrary initial mass imbalance and deformation field. The deformation frontogenesis solution of Hoskins & Bretherton (J. Atmos. Sci., vol. 29, 1972, pp. 11–37) and the mass imbalance solution of Blumen (J. Phys. Oceanogr., vol. 30, 2000, pp. 31–39) emerge as two limits of this general solution. Secondly, the problem of geostrophic adjustment of an initial mass imbalance (no deformation field) is considered for uniform PV flow bounded by rigid lids. The general solution is derived, composed of an adjusted state and a transient component describing the propagation of inertia–gravity waves. The criteria for the occurrence of a frontal discontinuity is determined in terms of the Rossby and Froude numbers. The uniform PV solution reduces identically to the zero PV solution of Blumen in the limit of vanishing background stratification. Thirdly, we examine the more general case of uniform PV flow with a deformation field and either balanced or unbalanced initial conditions. In this case the solution is composed of a time-varying mean state – matching the Hoskins & Bretherton solution in the limit of small strain – and an inertia gravity wave field, the dynamics of which are examined in detail. Our analysis provides a unifying framework capable of describing frontal formation and geostrophic adjustment in a wide variety of settings.