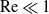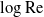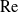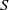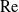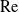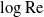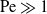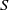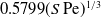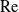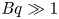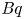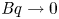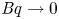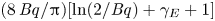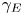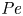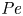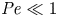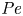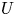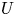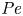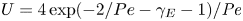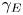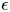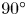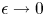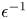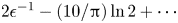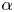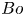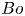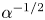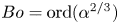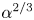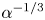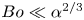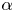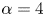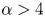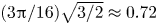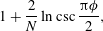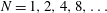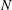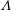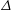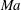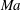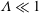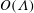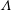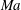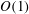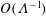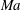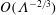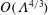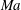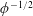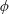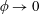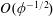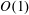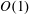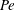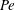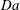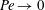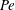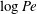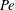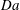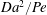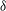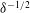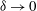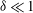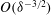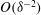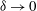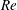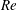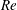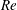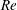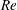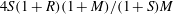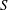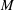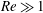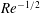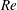A common realisation of superhydrophobic surfaces is based on a periodically grooved solid substrate, with air bubbles trapped in a Cassie state within the grooves. Following Baier, Steffes & Hardt (Phys. Rev. E, vol. 82 (3), 2010, 037301) we consider the thermocapillary flow of a liquid bounded between two such surfaces, driven by a macroscopic temperature gradient. Assuming zero protrusion angle of the free menisci, the periodic geometry is described by two parameters, namely the ratio 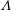 $\unicode[STIX]{x1D6EC}$ of the groove-array period to the channel depth and the gas fraction
$\unicode[STIX]{x1D6EC}$ of the groove-array period to the channel depth and the gas fraction 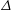 $\unicode[STIX]{x1D6E5}$ of the surface. The flow and heat transport depend upon both these parameters, as well as the Marangoni number
$\unicode[STIX]{x1D6E5}$ of the surface. The flow and heat transport depend upon both these parameters, as well as the Marangoni number 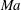 $Ma$, which quantifies the relative magnitudes of advection and conduction. This paper is concerned with the longitudinal problem, where the temperature gradient is applied along the grooves. The temperature within the highly conducting solid substrate varies linearly with distance and may be regarded as prescribed. For any non-zero value of
$Ma$, which quantifies the relative magnitudes of advection and conduction. This paper is concerned with the longitudinal problem, where the temperature gradient is applied along the grooves. The temperature within the highly conducting solid substrate varies linearly with distance and may be regarded as prescribed. For any non-zero value of 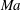 $Ma$, however, advection necessitates the formation of an excess temperature profile in the liquid domain, above and beyond that linearly varying distribution. The associated Marangoni forces, in turn, imply the formation of flow in the cross-sectional plane. The nonlinearly coupled problem governing the excess temperature and cross-sectional flow is independent of the longitudinal flow. Conversely, the latter satisfies an independent problem in the Stokes limit, and accordingly possesses the standard thermocapillary scaling. A simple transformation reveals a linkage between the longitudinal velocity in the present problem and that in the comparable pressure-driven flow. In studying the coupled problems governing the excess temperature and cross-sectional velocity components, we focus upon deep channels, where
$Ma$, however, advection necessitates the formation of an excess temperature profile in the liquid domain, above and beyond that linearly varying distribution. The associated Marangoni forces, in turn, imply the formation of flow in the cross-sectional plane. The nonlinearly coupled problem governing the excess temperature and cross-sectional flow is independent of the longitudinal flow. Conversely, the latter satisfies an independent problem in the Stokes limit, and accordingly possesses the standard thermocapillary scaling. A simple transformation reveals a linkage between the longitudinal velocity in the present problem and that in the comparable pressure-driven flow. In studying the coupled problems governing the excess temperature and cross-sectional velocity components, we focus upon deep channels, where 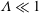 $\unicode[STIX]{x1D6EC}\ll 1$. Towards this end, we employ matched asymptotic expansions, with two
$\unicode[STIX]{x1D6EC}\ll 1$. Towards this end, we employ matched asymptotic expansions, with two 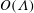 $O(\unicode[STIX]{x1D6EC})$-deep inner regions adjacent to the surfaces and an outer region in the remaining fluid domain. The small-
$O(\unicode[STIX]{x1D6EC})$-deep inner regions adjacent to the surfaces and an outer region in the remaining fluid domain. The small-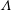 $\unicode[STIX]{x1D6EC}$ limit is compatible with two possible scalings of
$\unicode[STIX]{x1D6EC}$ limit is compatible with two possible scalings of 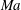 $Ma$, the first where it is
$Ma$, the first where it is 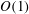 $O(1)$ and the second where it is
$O(1)$ and the second where it is 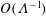 $O(\unicode[STIX]{x1D6EC}^{-1})$. In the first scaling, the excess temperature in the outer region is driven by a balance between longitudinal advection and conduction perpendicular to the bounding surfaces. In the inner region, the excess temperature is governed by pure conduction; the cross-sectional flow it animates, which possesses the thermocapillary scaling, is linear in
$O(\unicode[STIX]{x1D6EC}^{-1})$. In the first scaling, the excess temperature in the outer region is driven by a balance between longitudinal advection and conduction perpendicular to the bounding surfaces. In the inner region, the excess temperature is governed by pure conduction; the cross-sectional flow it animates, which possesses the thermocapillary scaling, is linear in 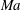 $Ma$. In the second scaling, the cross-sectional velocity becomes
$Ma$. In the second scaling, the cross-sectional velocity becomes 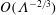 $O(\unicode[STIX]{x1D6EC}^{-2/3})$ large relative to the thermocapillary scaling; a boundary layer, of
$O(\unicode[STIX]{x1D6EC}^{-2/3})$ large relative to the thermocapillary scaling; a boundary layer, of 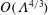 $O(\unicode[STIX]{x1D6EC}^{4/3})$ dimensionless width, is formed within the inner region. In that layer the excess temperature is governed by a dominant balance between conduction perpendicular to the surface and cross-sectional advection. The dependence upon
$O(\unicode[STIX]{x1D6EC}^{4/3})$ dimensionless width, is formed within the inner region. In that layer the excess temperature is governed by a dominant balance between conduction perpendicular to the surface and cross-sectional advection. The dependence upon 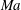 $Ma$ is inherently nonlinear.
$Ma$ is inherently nonlinear.