Published online by Cambridge University Press: 07 October 2019
The hydrodynamic quantification of superhydrophobic slipperiness has traditionally employed two canonical problems – namely, shear flow about a single surface and pressure-driven channel flow. We here advocate the use of a new class of canonical problems, defined by the motion of a superhydrophobic particle through an otherwise quiescent liquid. In these problems the superhydrophobic effect is naturally measured by the enhancement of the Stokes mobility relative to the corresponding mobility of a homogeneous particle. We focus upon what may be the simplest problem in that class – the rotation of an infinite circular cylinder whose boundary is periodically decorated by a finite number of infinite grooves – with the goal of calculating the rotational mobility (velocity-to-torque ratio). The associated two-dimensional flow problem is defined by two geometric parameters – namely, the number 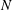 $N$ of grooves and the solid fraction
$N$ of grooves and the solid fraction 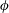 $\unicode[STIX]{x1D719}$. Using matched asymptotic expansions we analyse the large-
$\unicode[STIX]{x1D719}$. Using matched asymptotic expansions we analyse the large-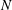 $N$ limit, seeking the mobility enhancement from the respective homogeneous-cylinder mobility value. We thus find the two-term approximation,
$N$ limit, seeking the mobility enhancement from the respective homogeneous-cylinder mobility value. We thus find the two-term approximation,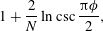 $$\begin{eqnarray}\displaystyle 1+{\displaystyle \frac{2}{N}}\ln \csc {\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}}{2}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1+{\displaystyle \frac{2}{N}}\ln \csc {\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}}{2}}, & & \displaystyle \nonumber\end{eqnarray}$$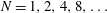 $N=1,2,4,8,\ldots$. We conjecture that it is exact for all
$N=1,2,4,8,\ldots$. We conjecture that it is exact for all 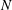 $N$.
$N$.