Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T07:27:17.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Small-solid-fraction approximations for the slip-length tensor of micropillared superhydrophobic surfaces

Published online by Cambridge University Press:  26 March 2018

Ory Schnitzer Open the ORCID record for Ory Schnitzer [Opens in a new window]  and
Ehud Yariv Open the ORCID record for Ehud Yariv [Opens in a new window]
Ory Schnitzer*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK
Ehud Yariv
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: o.schnitzer@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Fakir-like superhydrophobic surfaces, formed by doubly periodic arrays of thin pillars that sustain a lubricating gas layer, exhibit giant liquid-slip lengths that scale as 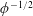$\unicode[STIX]{x1D719}^{-1/2}$ relative to the periodicity, 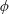$\unicode[STIX]{x1D719}$ being the solid fraction (Ybert et al., Phys. Fluids, vol. 19, 2007, 123601). Considering arbitrarily shaped pillars distributed over an arbitrary Bravais lattice, we employ matched asymptotic expansions to calculate the slip-length tensor in the limit 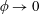$\unicode[STIX]{x1D719}\rightarrow 0$. The leading 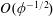$O(\unicode[STIX]{x1D719}^{-1/2})$ slip length is determined from a local analysis of an ‘inner’ region close to a single pillar, in conjunction with a global force balance. This leading term, which is independent of the lattice geometry, is related to the drag due to pure translation of a flattened disk shaped like the pillar cross-section; its calculation is illustrated for the case of elliptical pillars. The 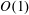$O(1)$ slip length is associated with the excess velocity induced about a given pillar by all the others. Since the field induced by each pillar corresponds on the ‘outer’ lattice scale to a Stokeslet whose strength is fixed by the shear rate, the 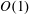$O(1)$ slip length depends upon the lattice geometry but is independent of the cross-sectional shape. Its calculation entails asymptotic evaluation of singular lattice sums. Our approximations are in excellent agreement with existing numerical computations for both circular and square pillars.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 637 - 652
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions, 3rd edn. Dover.Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–441.Google Scholar
Cottin-Bizonne, C., Barentin, C., Charlaix, É., Bocquet, L. & Barrat, J.-L. 2004 Dynamics of simple liquids at heterogeneous surfaces: molecular-dynamics simulations and hydrodynamic description. Eur. Phys. J. 15 (4), 427–438.Google Scholar
Davis, A. M. J. & Lauga, E. 2010 Hydrodynamic friction of fakir-like superhydrophobic surfaces. J. Fluid Mech. 661, 402–411.Google Scholar
Extrand, C. W. 2004 Criteria for ultralyophobic surfaces. Langmuir 20 (12), 5013–5018.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (2), 317–328.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Kittel, C. 2005 Introduction to Solid State Physics. Wiley.Google Scholar
Lamb, H. 1945 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Lee, C., Choi, C.-H. & Kim, C.-J. 2008 Structured surfaces for a giant liquid slip. Phys. Rev. Lett. 101 (6), 064501.Google Scholar
Ng, C.-O. & Wang, C. 2010 Apparent slip arising from Stokes shear flow over a bidimensional patterned surface. Microfluid. Nanofluid. 8 (3), 361–371.Google Scholar
Nijboer, B. R. A. & De Wette, F. W. 1957 On the calculation of lattice sums. Physica 23, 309–321.Google Scholar
Pozrikidis, C. 1996 Computation of periodic Green’s functions of Stokes flow. J. Engng Maths 30 (1–2), 79–96.Google Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38 (1), 71–99.Google Scholar
Ybert, C., Barentin, C., Cottin-Bizonne, C., Joseph, P. & Bocquet, L. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19 (12), 123601.Google Scholar