Article contents
Electrohydrodynamic rotation of drops at large electric Reynolds numbers
Published online by Cambridge University Press: 11 January 2016
Abstract
When subject to sufficiently strong electric fields, particles and drops suspended in a weakly conducting liquid exhibit spontaneous rotary motion. This so-called Quincke rotation is a fascinating example of nonlinear symmetry-breaking phenomena. To illuminate the rotation of liquid drops we here analyse the asymptotic limit of large electric Reynolds numbers, 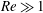 $\mathit{Re}\gg 1$ , within the framework of a two-dimensional Taylor–Melcher electrohydrodynamic model. A non-trivial dominant balance in this singular limit results in both the fluid velocity and surface-charge density scaling as
$\mathit{Re}\gg 1$ , within the framework of a two-dimensional Taylor–Melcher electrohydrodynamic model. A non-trivial dominant balance in this singular limit results in both the fluid velocity and surface-charge density scaling as 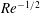 $\mathit{Re}^{-1/2}$ . The flow is governed by a self-contained nonlinear boundary-value problem that does not admit a continuous fore–aft symmetric solution, thus necessitating drop rotation. Furthermore, thermodynamic arguments reveal that a fore–aft asymmetric solution exists only when charge relaxation within the suspending liquid is faster than that in the drop. The flow problem possesses both mirror-image (with respect to the direction of the external field) and flow-reversal symmetries; it is transformed into a universal one, independent of the ratios of electric conductivities and dielectric permittivities in the respective drop phase and suspending liquid phase. The rescaled angular velocity is found to depend weakly upon the viscosity ratio. The corresponding numerical solutions of the exact equations indeed collapse at large
$\mathit{Re}^{-1/2}$ . The flow is governed by a self-contained nonlinear boundary-value problem that does not admit a continuous fore–aft symmetric solution, thus necessitating drop rotation. Furthermore, thermodynamic arguments reveal that a fore–aft asymmetric solution exists only when charge relaxation within the suspending liquid is faster than that in the drop. The flow problem possesses both mirror-image (with respect to the direction of the external field) and flow-reversal symmetries; it is transformed into a universal one, independent of the ratios of electric conductivities and dielectric permittivities in the respective drop phase and suspending liquid phase. The rescaled angular velocity is found to depend weakly upon the viscosity ratio. The corresponding numerical solutions of the exact equations indeed collapse at large 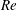 $\mathit{Re}$ upon the asymptotically calculated universal solution.
$\mathit{Re}$ upon the asymptotically calculated universal solution.
Information
- Type
- Rapids
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 18
- Cited by

