Alice of ‘wonderland’ and ‘looking glass’ fame is a creation of mathematician Charles Dodgson, better known by his pseudonym Lewis Carroll. In Glaister’s article Alice’s adventures in inverse tan land – mathematical argument, language and proof in the November 2019 Edition of The Mathematical Gazette readers are reminded of one of the exchanges in Alice’s Adventures in Wonderland (often shortened to Alice in Wonderland) which goes as follows:

“Would you tell me, please, which way I ought to go from here?”
“That depends a good deal on where you want to get to,” said the Cat.
“I don’t much care where–” said Alice.
“Then it doesn’t matter which way you go,” said the Cat.
“–so long as I get SOMEWHERE,” Alice added as an explanation.
“Oh, you’re sure to do that,” said the Cat, “if you only walk long enough.”

Glaister thinks that Alice would relish being at school in the 21^st century with the many opportunities to go on voyages of discovery through being immersed in problem-solving activities that are part and parcel of the current mathematics curriculum in schools.

One area of mathematics that Alice knew something of involved relationships with opposites – or the inverse tangent function, namely tan^-1 or arctan, for example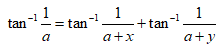, where xy = a² + 1, as cited in Abeles’ paper Charles L. Dodgson’s Geometric Approach to Acrtangent relations for Pi.

This relation can be written as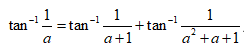, where , and which is a special case of 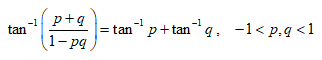, with  and  where -1<p,q<1. Alice could then use this relation to discover the (now) well-known result.

Glaister’s article explores generalisations of this result – which Alice would almost certainly have encountered on her travels if she had focussed more on mathematics than tea parties – including likely diversions along two particular tangents (or should we say inverse tangents, but not in verse!) beginning with this starting point, to discover, for example, that both ofandare integer multiples of π.

What would the Queen would have made of all this?

Alice’s adventures in inverse tan land – mathematical argument, language and proof will be free to access through 30th April 2020.