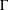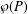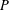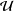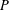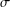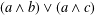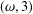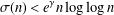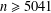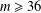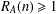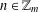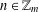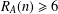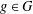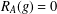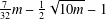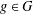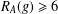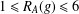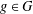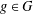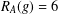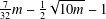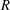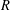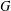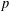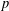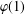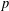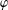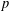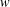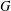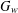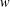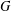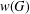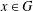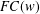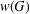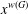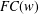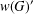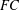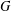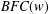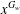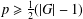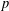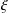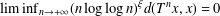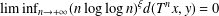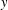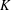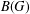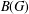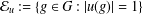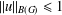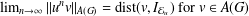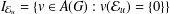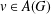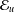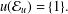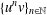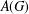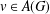Research Article
TWO NEW LOWER BOUNDS FOR THE SPARK OF A MATRIX
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2017, pp. 353-360
-
- Article
-
- You have access
- Export citation
CLOSURE OPERATORS, FRAMES AND NEATEST REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2017, pp. 361-373
-
- Article
-
- You have access
- Export citation
A NEW UPPER BOUND FOR THE SUM OF DIVISORS FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2017, pp. 374-379
-
- Article
-
- You have access
- Export citation
ON ADDITIVE REPRESENTATION FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 380-388
-
- Article
-
- You have access
- Export citation
CONGRUENCE OF SYMMETRIC INNER PRODUCTS OVER FINITE COMMUTATIVE RINGS OF ODD CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2017, pp. 389-397
-
- Article
-
- You have access
- Export citation
CM FIELDS WITHOUT UNIT-PRIMITIVE ELEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 20 September 2017, pp. 398-399
-
- Article
-
- You have access
- Export citation
THE SHORT RESOLUTION OF A SEMIGROUP ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 29 August 2017, pp. 400-411
-
- Article
-
- You have access
- Export citation
SYMMETRIC SQUARE-CENTRAL ELEMENTS IN PRODUCTS OF ORTHOGONAL INVOLUTIONS IN CHARACTERISTIC TWO
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 412-425
-
- Article
-
- You have access
- Export citation
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2017, pp. 426-428
-
- Article
-
- You have access
- Export citation
ON GROUPS WITH FINITE CONJUGACY CLASSES IN A VERBAL SUBGROUP
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2017, pp. 429-437
-
- Article
-
- You have access
- Export citation
REGULAR ORBITS OF COPRIME LINEAR GROUPS IN LARGE CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 438-444
-
- Article
-
- You have access
- Export citation
SOME REVERSE DYNAMIC INEQUALITIES ON TIME SCALES
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 445-454
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC AUTOMORPHISMS AND PROPER HOLOMORPHIC SELF-MAPPINGS OF A TYPE OF GENERALISED MINIMAL BALL
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2017, pp. 455-467
-
- Article
-
- You have access
- Export citation
ITERATED LOGARITHM SPEED OF RETURN TIMES
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2017, pp. 468-478
-
- Article
-
- You have access
- Export citation
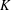 $K$-SPHERICAL FUNCTIONS ON ABELIAN SEMIGROUPS
$K$-SPHERICAL FUNCTIONS ON ABELIAN SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2017, pp. 479-486
-
- Article
-
- You have access
- Export citation
SOME CONVERGENCE THEOREMS IN FOURIER ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2017, pp. 487-495
-
- Article
-
- You have access
- Export citation
FUNCTIONAL VERSIONS OF SOME REFINED AND REVERSED OPERATOR MEAN INEQUALITIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2017, pp. 496-503
-
- Article
-
- You have access
- Export citation
A SCHWARZ LEMMA FOR
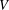 $V$-HARMONIC MAPS AND THEIR APPLICATIONS
$V$-HARMONIC MAPS AND THEIR APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 504-512
-
- Article
-
- You have access
- Export citation
A SPECIAL CLASS OF QUASI-CYCLIC CODES
- Part of:
-
- Published online by Cambridge University Press:
- 10 August 2017, pp. 513-518
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
DYNAMICS OF MATHEMATICAL MODELS FOR BIOREACTORS
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 519-520
-
- Article
-
- You have access
- Export citation