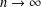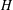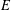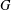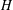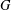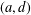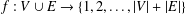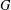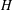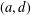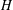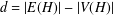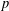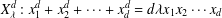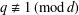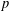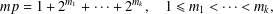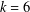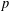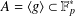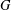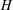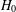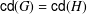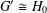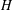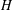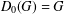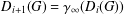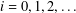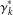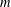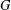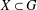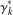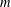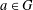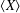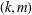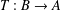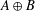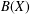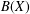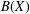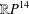Research Article
ENUMERATION OF A DUAL SET OF STIRLING PERMUTATIONS BY THEIR ALTERNATING RUNS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 177-186
-
- Article
-
- You have access
- Export citation
THERE ARE ASYMPTOTICALLY THE SAME NUMBER OF LATIN SQUARES OF EACH PARITY
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2016, pp. 187-194
-
- Article
-
- You have access
- Export citation
A SUFFICIENT CONDITION FOR A PAIR OF SEQUENCES TO BE BIPARTITE GRAPHIC
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2016, pp. 195-200
-
- Article
-
- You have access
- Export citation
ON
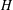 $H$-ANTIMAGICNESS OF DISCONNECTED GRAPHS
$H$-ANTIMAGICNESS OF DISCONNECTED GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 201-207
-
- Article
-
- You have access
- Export citation
COUNTING POINTS ON DWORK HYPERSURFACES AND
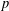 $p$-ADIC HYPERGEOMETRIC FUNCTIONS
$p$-ADIC HYPERGEOMETRIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
-
- Article
-
- You have access
- Export citation
ABSOLUTELY ABNORMAL AND CONTINUED FRACTION NORMAL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2016, pp. 217-223
-
- Article
-
- You have access
- Export citation
ALMOST ALL PRIMES HAVE A MULTIPLE OF SMALL HAMMING WEIGHT
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2016, pp. 224-235
-
- Article
-
- You have access
- Export citation
REFINEMENTS OF THE FIRST AND SECOND POSITIVE CRANK MOMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 236-244
-
- Article
-
- You have access
- Export citation
ON REAL PARTS OF POWERS OF COMPLEX PISOT NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2016, pp. 245-253
-
- Article
-
- You have access
- Export citation
GROUPS WITH THE SAME CHARACTER DEGREES AS SPORADIC ALMOST SIMPLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2016, pp. 254-265
-
- Article
-
- You have access
- Export citation
NORMAL SUBGROUPS WHOSE CONJUGACY CLASS GRAPH HAS DIAMETER THREE
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2016, pp. 266-272
-
- Article
-
- You have access
- Export citation
BOUNDING THE ORDER OF THE NILPOTENT RESIDUAL OF A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 273-277
-
- Article
-
- You have access
- Export citation
GENERAL STABILITY OF THE EXPONENTIAL AND LOBAČEVSKIǏ FUNCTIONAL EQUATIONS
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 278-285
-
- Article
-
- You have access
- Export citation
TRIVIALITY OF THE GENERALISED LAU PRODUCT ASSOCIATED TO A BANACH ALGEBRA HOMOMORPHISM
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 286-289
-
- Article
-
- You have access
- Export citation
THE LOGARITHMIC FUNCTION AND TRACE ZERO ELEMENTS IN FINITE VON NEUMANN FACTORS
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 290-295
-
- Article
-
- You have access
- Export citation
MORE ON THE ARENS REGULARITY OF
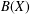 $B(X)$
$B(X)$
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 296-303
-
- Article
-
- You have access
- Export citation
ALMOST NONNEGATIVE CURVATURE ON SOME FAKE 6- AND 14-DIMENSIONAL PROJECTIVE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2016, pp. 304-315
-
- Article
-
- You have access
- Export citation
ON THE FIRST EIGENCONE FOR THE FINSLER LAPLACIAN
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2016, pp. 316-325
-
- Article
-
- You have access
- Export citation
ON GEHRING–MARTIN–TAN GROUPS WITH AN ELLIPTIC GENERATOR
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 326-336
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
THREE STUDIES IN HIGHER CATEGORY THEORY: FIBRATIONS, SKEW-MONOIDAL STRUCTURES AND EXCISION OF EXTREMALS
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2016, pp. 337-338
-
- Article
-
- You have access
- Export citation